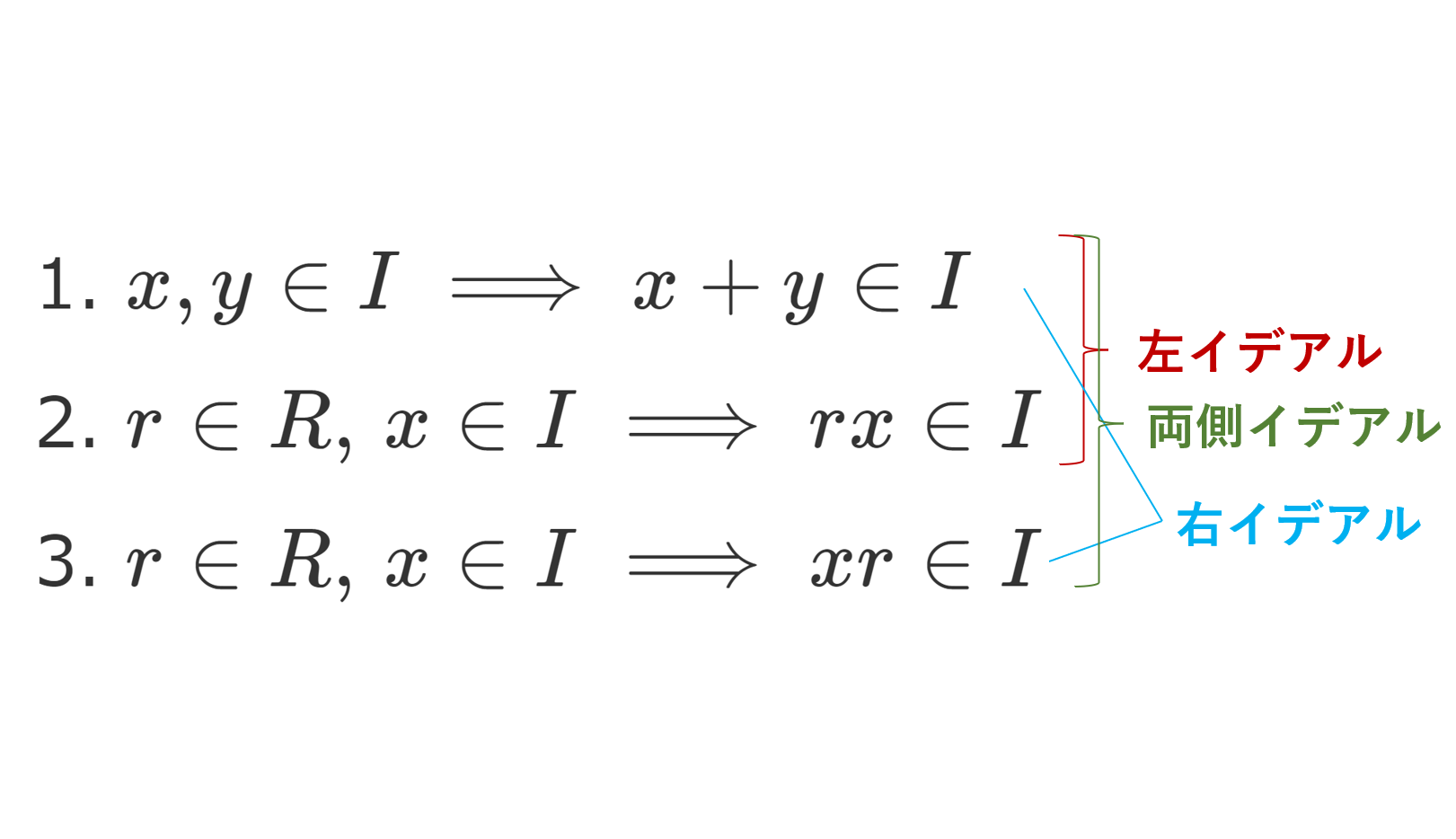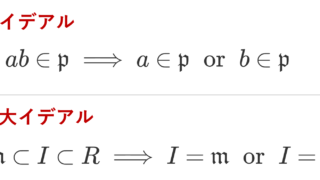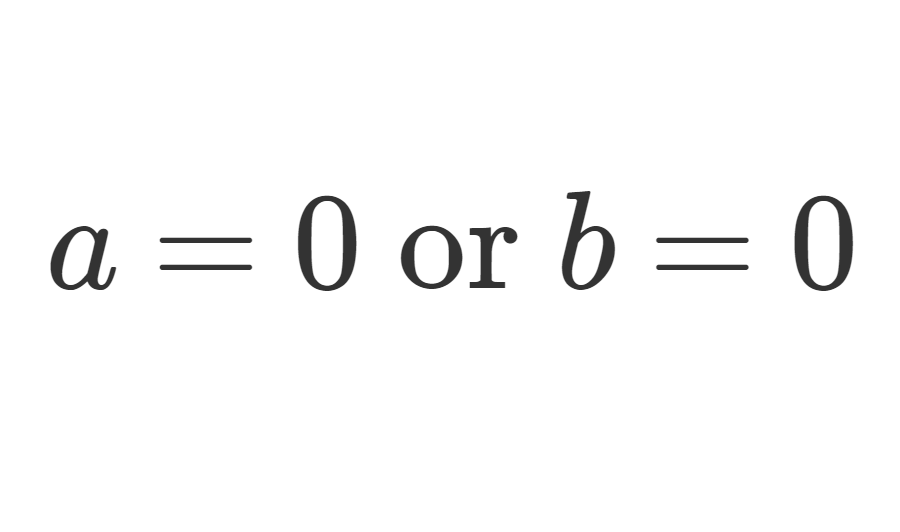代数学,特に環論における左イデアル・右イデアル・両側イデアルとは,それぞれ左・右・両側から元をかけても不変な,乗法単位元を持たなくても良い部分環のことを言います。群でいう正規部分群に対応する,環論における重要な概念です。
イデアルについて,その定義と具体例・性質について順番に解説していきましょう。
イデアルとは
以下で,環は単位的,すなわち乗法単位元 1 が存在するとし,零環(自明な環)でないとします。
定義(イデアル)
R を環とし, I\subset R とする。 I について,
- I は加法について部分群である。
- \color{red} r\in R,\, x\in I \implies rx\in I
- \color{red} r\in R,\, x\in I \implies xr\in I
のうち,1,2が成り立つとき I を左イデアル (left ideal) といい,1,3が成り立つとき I を右イデアル (right ideal) といい,1,2,3が成り立つとき,両側イデアル (two-sided ideal) という。
R が可換環のときは,2と3は同値になるから,左イデアルと右イデアルの区別はなく,単にイデアル (ideal) という。
イデアルは定義より明らかに部分環です(乗法単位元はないかもしれない)。イデアルは部分環よりも良い性質を持っていますね。群でいう,正規部分群に対応する概念が,環でいうイデアルと思っておけばよいです。
1.の条件は単に \color{red} x,y\in I\implies x+y\in I (加法について閉じている)と言い換えても良いです。
実際,2,3.の条件と, 0x=x0=0, \, (-1)x=x(-1)=-x から, 0\in I と x\in I \implies -x\in I もわかるので,部分群の判定法より, I は加法について部分群だとわかるからです。
イデアルの具体例
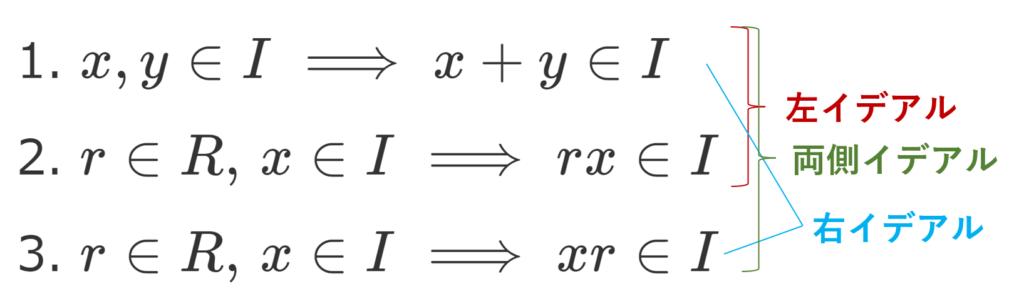
例1.
環 R において, \{0\}, R はそれぞれ(両側)イデアルである。これを自明なイデアル (trivial ideal) という。
自明なイデアルでないイデアルを真のイデアル (proper ideal) という。
例2.
3 の倍数の集合 3\mathbb{Z}\subset\mathbb{Z} は,可換環 \mathbb{Z} におけるイデアルである。
3の倍数の和は3の倍数であり,また左右から整数をかけても,それは3の倍数ですから,3の倍数全体の集合は整数 \mathbb{Z} におけるイデアルになります。
同様に, a\in\mathbb{Z} に対し, a の倍数全体の集合 a\mathbb{Z} もイデアルです。
例3.
整数係数多項式全体の集合のなす可換環
\mathbb{Z}[x]=\left\{ \sum_{k=0}^n a_kx^k\middle| a_k\in\mathbb{Z},n\ge 0\right\}
について,
はどちらもイデアルである。
これもイデアルの例ですね。 3\mathbb{Z}[x] は係数が常に3の倍数で, x\mathbb{Z}[x] は定数項を持たないものの集合です。
例4.
実数成分の2次正方行列のなす行列環 \mathrm{M}_2(\mathbb{R}) について,
I= \left\{ \begin{pmatrix} x & 0\\ y& 0\end{pmatrix}\middle| x,y\in\mathbb{R} \right\}
は左イデアルであり,
は右イデアルである。
非可換環における左イデアル・右イデアルの例ですね。
イデアルの性質
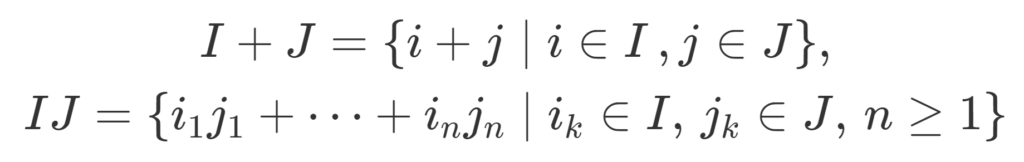
定理(イデアルの性質)
R,S を環とする。このとき,
- I\subset R が左イデアル(右イデアル)かつ 1\in I ならば, I=R である。
- 体は自明なイデアルしか持たない。逆に,自明なイデアルしか持たない可換環は体である。
- f\colon R\to S を準同型とするとき, \operatorname{Ker} f は R の両側イデアルである。
- f\colon R\to S を準同型, J\subset S を左イデアル(右イデアル)とするとき, \emptyset \ne f^{-1}(J)\subset R ならば,これは R の左イデアル(右イデアル)である。
- I, J\subset R を左イデアル(右イデアル)とするとき, I\cap J,
IJ=\{ ij\mid i\in I,\,j\in J\} としてしまうと,加法について閉じなくなってしまうので,上の定義のようにしています。
順番に証明していきましょう。
1. 乗法単位元1を含むイデアルはRに一致
証明
1\in I\subset R を左イデアルとする。このとき, r\in R に対し, r1=r\in I となるから, I=R である。 右イデアルも同様である。
証明終
2. 体は自明なイデアルしか持たず,逆も成立
証明
K を体, \{0\}\ne I\subset K をイデアルとする。このとき, x\in I\setminus \{0\} に対して, K は体より x^{-1}\in K が存在する。 I はイデアルより, 1=x^{-1}x \in I である。故に,1.より, I=K となり,結局 I は自明なイデアルである。
また,逆に可換環 R が自明なイデアルしか持たないとする。 0\ne r\in R に対し, (r)=\{ar\mid a\in R\} は自明なイデアルなので, 1\in (r) である。特に, r^{-1}r=1 となる乗法逆元 r^{-1} が存在する。よって, R は体である。
証明終
3. Ker f は両側イデアル
\operatorname{Ker } f = \{ x\in R\mid f(x)=0\}
です。
証明
x,y\in \operatorname{Ker} f とする。このとき,
f(x+y)=f(x)+f(y)=0+0=0
であるから, x+y\in\operatorname{Ker} f が成り立つ。また, r\in R に対し,
であるから, rx,xr\in \operatorname{Ker} f となり, \operatorname{Ker} f は両側イデアルである。
証明終
群のとき, \operatorname{ker} f は正規部分群でしたから,準同型の核(Ker) は群のときも環のときも非常に良い性質を持っているわけですね。
4. 左イデアルの準同型による引き戻しは左イデアル
同じことなので,左イデアルの場合のみ示しましょう。
証明
f\colon R\to S を準同型, J\subset S を左イデアル, f^{-1}(J)\ne \emptyset とする。 x,y\in f^{-1}(J) に対し,
f(x+y)=f(x)+f(y)\in J
より, x+y\in f^{-1}(J) である。また, x\in f^{-1}(J), \,r\in R に対し, J\subset S は左イデアルであるので,
であるから, rx\in f^{-1}(J) である。
証明終
5. イデアルの共通部分・和・積もイデアル
\begin{gathered}I+J=\{ i+j\mid i\in I\, ,j\in J\}, \\ IJ = \{ i_1j_1+\dots + i_nj_n\mid i_k\in I,\, j_k\in J,\,n\ge 1\} \end{gathered}を思い出しましょう。これらが左イデアルであることを示します。
証明
同じことなので,左イデアルのときのみ示す。 I\cap J が左イデアルなのは明らか。
I+J について,これは加法について閉じていることは簡単にわかる。 i+j\in I+J とする。 r\in R に対し, I, J は左イデアルなので, ri\in I,\, rj\in J である。ゆえに,
r(i+j)=ri+rj\in I+J
となり, I+J は左イデアルである。
IJ について,これが加法について閉じていることは簡単にわかる。 i_1j_1+\cdots +i_nj_n \in IJ とする。 r\in R に対し,
r(i_1j_1+\cdots +i_nj_n)=(ri_1)j_1+\cdots +(ri_n)j_n
である。 I は左イデアルなので, ri_1,\dots, ri_n\in I より,上の式は IJ に含まれる。従って, IJ も左イデアルである。
証明終
たとえば, \mathbb{Z} におけるイデアルについて,
\begin{aligned}6\mathbb{Z}\cap 9 \mathbb{Z} &=18 \mathbb{Z},\\ 6\mathbb{Z} + 9\mathbb{Z}&=3 \mathbb{Z} ,\\ (6 \mathbb{Z} )(9 \mathbb{Z} )&=54 \mathbb{Z} \end{aligned}
となります。
イデアルの生成
ここからは環は全て可換環とし,左イデアル・右イデアルを区別せず扱います。
I,J がイデアルであるとき, I\cap J もイデアルであると述べました。同様に, \{I_\lambda\} をイデアルの族とすると, \bigcap_{\lambda} I_\lambda もイデアルになります。
R を可換環, S\subset R を部分集合としましょう。このとき, S を含むイデアル全体の集合を
\mathscr{I}_S=\{ S\subset I\mid I \text{ is an ideal}\}
としましょう。 R\in \mathscr{I}_S より, \mathscr{I}_S は空ではありません。ここで,
とすると, (S) も, S を含むイデアルであり,特に S を含む最小のイデアルになります。このように,ある集合に対し,それを含む「最小のイデアル」を考えることが可能です。これが,イデアルの生成です。
定義(イデアルの生成)
R を可換環とし, S\subset R をその部分集合とする。 S を含む最小のイデアルを \color{red} (S) と表し, S で生成されたイデアルという。このときの S の各元を生成元という。
特に,一つの元で生成されるイデアルを単項イデアル (principal ideal) ,有限個の元で生成されるイデアルを有限生成イデアル (finitely generated ideal) という。
(S) は一般に
\color{red} (S)=\{ r_1s_1+\dots +r_ns_n\mid r_k\in R,s_k\in S, n\ge 1\}
という形をしています(今は可換環であることに注意)。実際, (S) がイデアルの定義をみたすことと, S を含むイデアルは必ず (S) の元を含まなければならないことが容易にわかるため,このことは簡単に確認可能です。特に, S=\{s_1,s_2,\dots, s_n\} が有限集合のときは,単に
とかけ,右辺を単に Rs_1+\dots +Rs_n と書くことがあります。
ここで,イデアルの生成は普通 (S) のように,括弧を用いて表すのが普通です。大学数学では,括弧をさまざまなところで使うので,少々ややこしいですね。文脈判断しかないです。
この記法を用いると,例3で現れる \mathbb{Z}[x] 上の2つのイデアルはそれぞれ (3),(x) とかけます。
さらに進んだ概念
イデアルに関連する,さらなる概念を箇条書きしておきます。
- 素イデアル …… ab\in \mathfrak{p}\implies a\in \mathfrak{p}\text{ or } b\in\mathfrak{p} をみたすイデアル \mathfrak{p} のこと(素数の概念に対応)
- 極大イデアル …… 真のイデアルのうち,包含関係に関して極大のもの
これらは以下で解説しています。