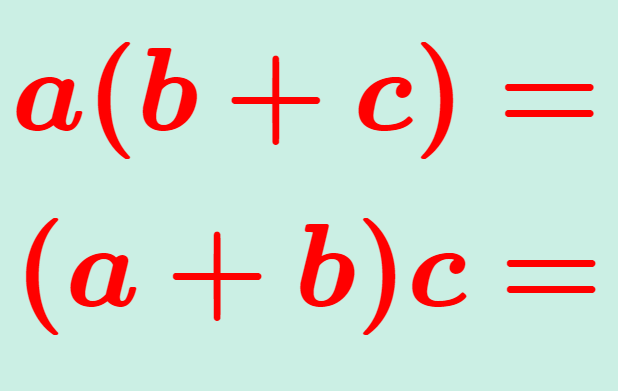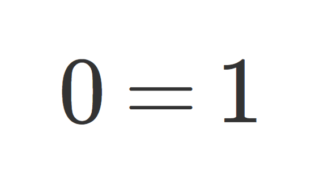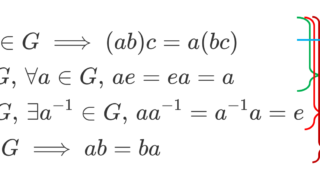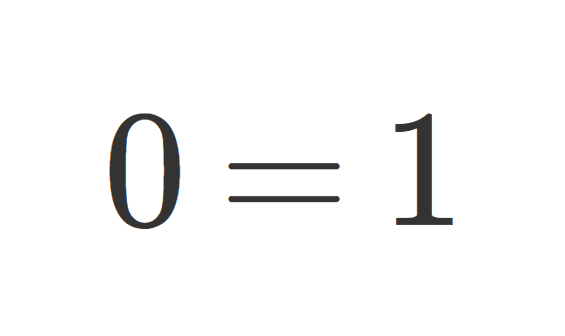代数学における,環・可換環とは,足し算と掛け算を考えられる集合を指します。環の定義・可換環の定義について述べ,その具体例も挙げていきましょう。
環の定義・可換環の定義
定義(環・可換環)
(R,+,\times) について,二つの二項演算 + (加法・和), \times (乗法・積)が定義されていて,(以下 a\times b は ab とかく)
- (R,+) は可換群(アーベル群)である。すなわち,
a. \color{red}\boldsymbol{(a+b)+c=a+(b+c)} (結合法則)
b. \color{red}\boldsymbol{a+0=0+a=a} (加法単位元 0 の存在)
c. \color{red}\boldsymbol{a+(-a)=(-a)+a=0} (加法逆元 -a の存在)
d. \color{red} \boldsymbol{a+b=b+a} (可換性) - (R,\times) はモノイドである。すなわち,
a. \color{red} \boldsymbol{(ab)c=a(bc)} (結合法則)
b. \color{red}\boldsymbol{1a=a1=a} (乗法単位元 1 の存在) - +,\times の間の分配法則,すなわち,
a. \color{red}\boldsymbol{ a(b+c)=ab+ac}
b. \color{red}\boldsymbol{ (a+b)c=ac+bc}
が成り立つとき,環 (ring) という。
さらに乗法について \boldsymbol{\color{red}ab=ba} (可換性)が成り立つとき,可換環 (commutative ring) という。
a,b\in R なら a+b,ab\in R です(二項演算の前提)。これをそれぞれ加法,乗法に関して閉じているといいます。
環の定義には,乗法単位元 1 の存在を仮定しないこともあります。 1 があるような環を単位的 (unital) ということがあります。
群よりさらに良い性質を持っているのが環です。群のときと同様,定義が非常に抽象的ですね。抽象的であるが故に,さまざまな集合上の演算を統一的に扱えるというのが最大のメリットです。
環は,乗法についての逆元の存在 ( a に対し, aa^{-1}=a^{-1}a=1 となる a^{-1} の存在)を仮定していません。よって,このような a^{-1} \in R は存在しなくても構いませんが,逆にこのような a^{-1}\in R があるような元 a \in R を R の単元 (unit) または可逆元 (invertible element) といいます。
具体例を確認していきましょう。
環・可換環の具体例
例1(整数環).
\mathbb{Z} は通常の加法 + と乗法 \times に関して可換環である。
加法単位元は 0\in\mathbb{Z} で,乗法単位元は 1\in\mathbb{Z} である。
整数全体の集合 \mathbb{Z} は,足し算と掛け算について閉じていて,かつ分配法則などの各規則が成り立ち,さらに ab=ba ですから可換環です。同じ理由で \mathbb{Q},\mathbb{R},\mathbb{C} も可換環です。
このとき, \mathbb{Z} の単元(可逆元)は \pm 1 のみですが, \mathbb{Q,R,C} の単元(可逆元)はそれぞれ \mathbb{Q}\setminus\{0\},\mathbb{R}\setminus\{0\},\mathbb{C}\setminus \{0\} ですね。
整数は環の最も基本的な例です。むしろ,整数の概念を一般化したのが環であると言ってもよいでしょう。
例2(多項式環).
整数係数多項式全体の集合
\mathbb{Z}[x]=\left\{\sum_{k=0}^n a_kx^n\middle| a_k\in\mathbb{Z},\,n\ge 1\right\}
は,通常の加法 + と乗法 \times に関して可換環である。
加法単位元は 0\in\mathbb{Z}[x] で,乗法単位元は 1\in\mathbb{Z}[x] である。
まず,整数係数多項式の和や積も整数係数多項式ですから,和と積について閉じています。そして,演算は可換環の各定義を満たしていますね。
例3(連続関数).
\mathbb{R} 上関数全体の集合 C(\mathbb{R}) は f,g\in C(\mathbb{R}) に対し,和と積を
\begin{aligned} (f+g)(x)&=f(x)+g(x) \\ (fg)(x)&=f(x)g(x)\end{aligned}
と定めることにより,可換環となる。
加法単位元は 0\in C(\mathbb{R}) で,乗法単位元は 1\in C(\mathbb{R}) である。
f,g が連続関数のとき, f+g,fg も連続関数ですから,和・積に関して閉じています。そして,演算は可換環の各定義を満たしていますね。
例4(行列環).
実数を各成分に持つ n 次正方行列全体の集合 M_n(\mathbb{R}) は通常の加法・乗法に関して環であるが,可換ではない。
加法単位元は零行列 O\in M_n(\mathbb{R}) で,乗法単位元は単位行列 I\in M_n(\mathbb{R}) である。
行列環は可換でない環の典型例といえるでしょう。
例5.
3の倍数全体の集合 3\mathbb{Z} は,通常の加法・乗法に関して,乗法単位元のない可換環である。
乗法単位元 1 がない環の簡単な例ですね。
例6(零環).
R=\{0\} は加法と乗法を
\begin{aligned}0+0&=0,\\ 0\times 0&=0 \end{aligned}
と定めることで可換環となる。これを零環 (the zero ring) または自明な環 (trivial ring) という。
零環は,加法単位元と乗法単位元が一致する唯一の環です。零環(自明な環)とは~0=1をみたす唯一の環であることの証明~で詳しく解説しています。
環の基本的な性質
環の基本的な性質を挙げましょう。
定理(環の基本的な性質)
R を環とする。このとき,
- 0a=a0=0,\quad a\in R
- (-1)a = -a,\quad a\in R
1.は加法単位元との積を考えています。2.は乗法単位元 1 の加法についての逆元 -1 を a にかけると, a の逆元になると言っています。
この他に,環の加法単位元 0,乗法単位元 1 は一意です。これは,加法群(可換群)・モノイドにおいてそれぞれ加法単位元・乗法単位元が一意であることから従います(→群の定義・可換群(アーベル群)の定義と具体例6つをていねいにで証明しています)。
証明
1. 0a=a0=0 について
0a= (0+0)a = 0a+0a より, 0a=0 である。 a0=0 も同様である。
2. (-1)a=-a について
0=0a=(1+(-1))a=a+(-1)a と, 0=a0=a(1+(-1))=a+(-1)a より, (-1)a=-a である。
証明終