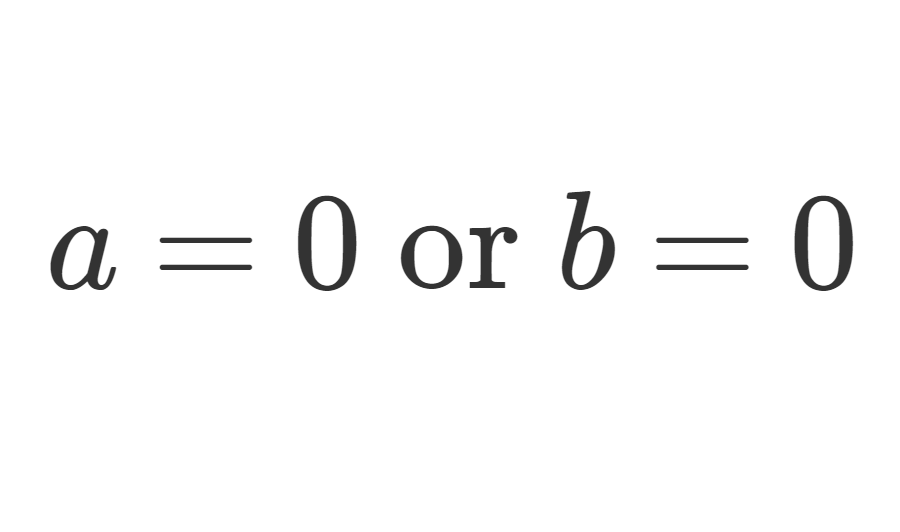整域とは～定義・具体例4つ・基本的性質4つ～

整域とは，零因子が $0$ しかない可換環のことをいいます。すなわち， $ab=0$ ならば， $a=0$ または $b=0$ が成り立ちます。

整域について，その定義と具体例・そして基本的性質4つの証明を行いましょう。

なお，本記事では一貫して，環は乗法単位元を持ち，零環(自明な環)でないとします。

整域とは
整域とそうでない例
整域の基本的な性質
さらに進んだ概念
関連する記事

整域とは

整域は，可換環に対して定義するのが普通です。

定義（整域）

可換環 $R$ が整域 (integral domain; entire ring) であるとは， $a,b\in R$ に対し

\color{red}\large ab=0 \implies a=0 \text{ or } b=0

が成り立つことをいう。

$a\in R$ に対し，ある $b\in R$ があって $ab=0$ とできるとき， $a$ を零因子 (zero divisor) といいます。整域とは，零因子が $0$ しかない環のことを指します。定義は対偶を取って，

\Large a,b \ne 0\implies ab\ne 0

と思っても構いません。

とにかくスグに具体例を確認してきましょう。

整域とそうでない例

例1.

可換環 $\mathbb{Z,Q,R,C}$ は全て整域である。

いわゆる「数」は整域ですね。

よく高校生が， $x^2+2x-3=0$ を解くのに， $(x+3)(x-1)=0$ とやって， $x=-3, 1$ と解きますが，これは複素数が整域であることを使っています。

例2.

可換環 $\mathbb{Z}^2$ は整域でない。たとえば，

(0,2) \times (1, 0)= (0,0)

である。

他にも $n \ge 2$ に対し， $\mathbb{Z}^n,\mathbb{Q}^n,\mathbb{R}^n ,\mathbb{C}^n$ や，他にも $\mathbb{Z}\times \mathbb{R}$ などは整域ではありません。

例3.

通常の和・積を備えた関数全体の集合のなす可換環 $F(\mathbb{R})$ は整域でない。たとえば，

1_{(0,\infty)} \times 1_{(-\infty,0)}=0

である。ただし， $1_{\cdot}$ は定義関数(指示関数)を表す。

例4.

可換環 $\mathbb{Z}/4\mathbb{Z}$ ( ${}\bmod 4$ の世界) は整域でない。たとえば， $\overline{2}\in \mathbb{Z}/4\mathbb{Z}$ に対し，

\overline{2}\times \overline{2}=\overline{0}

である。ただし， $\mathbb{Z}/4\mathbb{Z} =\{\overline{0}, \overline{1} , \overline{2} , \overline{3} \}$ とした。

$\mathbb{Z}/4\mathbb{Z}$ は整域ではありません。一方で，たとえば $\mathbb{Z}/3\mathbb{Z}$ は整域になります。

整域の基本的な性質

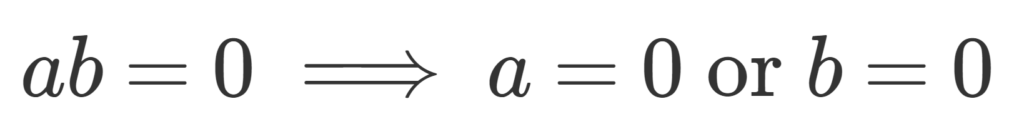
整域の基本的な性質4つを紹介し，その証明をしておきましょう。

定理（整域の基本的な性質）

整域の部分環は整域である。
体は整域である。
有限整域(有限集合の整域)は体である。
$A$ が整域のとき， $A[x_1,x_2,\dots, x_n]$ ( $A$ 係数 $n$ 変数多項式)も整域である。

順番に証明していきましょう。

証明

1. 整域の部分環は整域であること

明らか。

2. 体は整域であること

$ab=0$ かつ $a\ne 0$ とする。体は $0$ でない元について，その乗法逆元 $a^{-1}$ が存在する。 $ab=0$ の両辺に $a^{-1}$ をかけて $b=a^{-1}0=0$ である。

3. 有限整域は体であること

$R=\{0, a_1,a_2,\dots, a_n\}$ を整域 ( $a_i$ は全て $0$ でなく，どの2つも異なる) とする。 $a\ne 0$ に対し，

aa_1, aa_2, \dots, aa_n

を考える。 $R$ は整域で， $a,a_i\ne 0$ より， $aa_i\ne 0$ である。また， $i\ne j$ に対し， $a_i-a_j\ne 0$ より， $a(a_i-a_j) \ne 0$ すなわち $aa_i\ne aa_j$ である。

ゆえに， $aa_1, aa_2, \dots, aa_n$ の中には， $a_1,a_2,\dots, a_n$ が一つずつ現れる。特に， $aa_r=1$ となる $r$ が存在する。これは $a^{-1}$ の存在を意味し， $R$ は体である。

4. $A$ が整域ならば $A[x_1,x_2,\dots, x_n]$ も整域であること

$A$ が整域ならば， $A[x]$ も整域であること示せば， $A[x_1,\dots, x_n]=A[x_1,\dots, x_{n-1}][x_n]$ と帰納法により従う。よって青字を示す。

$f(x),g(x)\in A[x]$ として， $f(x)g(x)=0$ とする。 $f(x),g(x)$ の最高次項をそれぞれ $a_kx^k, b_lx^l\; (a_k, b_l\ne 0)$ とすると， $A$ は整域より， $a_kb_l\ne 0$ であり， $f(x)g(x)$ の最高次項は $a_kb_l x^{k+l}$ である。よって， $k=l=0$ である。

ゆえに， $f(x), g(x)\in A$ であり， $A$ は整域だから， $f(x)=0$ または $g(x)=0$ となる。したがって， $A[x]$ も整域である。

証明終

他にも，可換環 $R$ に対して， $I\subset R$ が素イデアルであることの必要十分条件は $R/I$ が整域であることです。この証明は，以下で行っています。