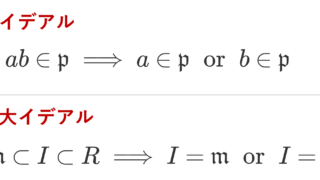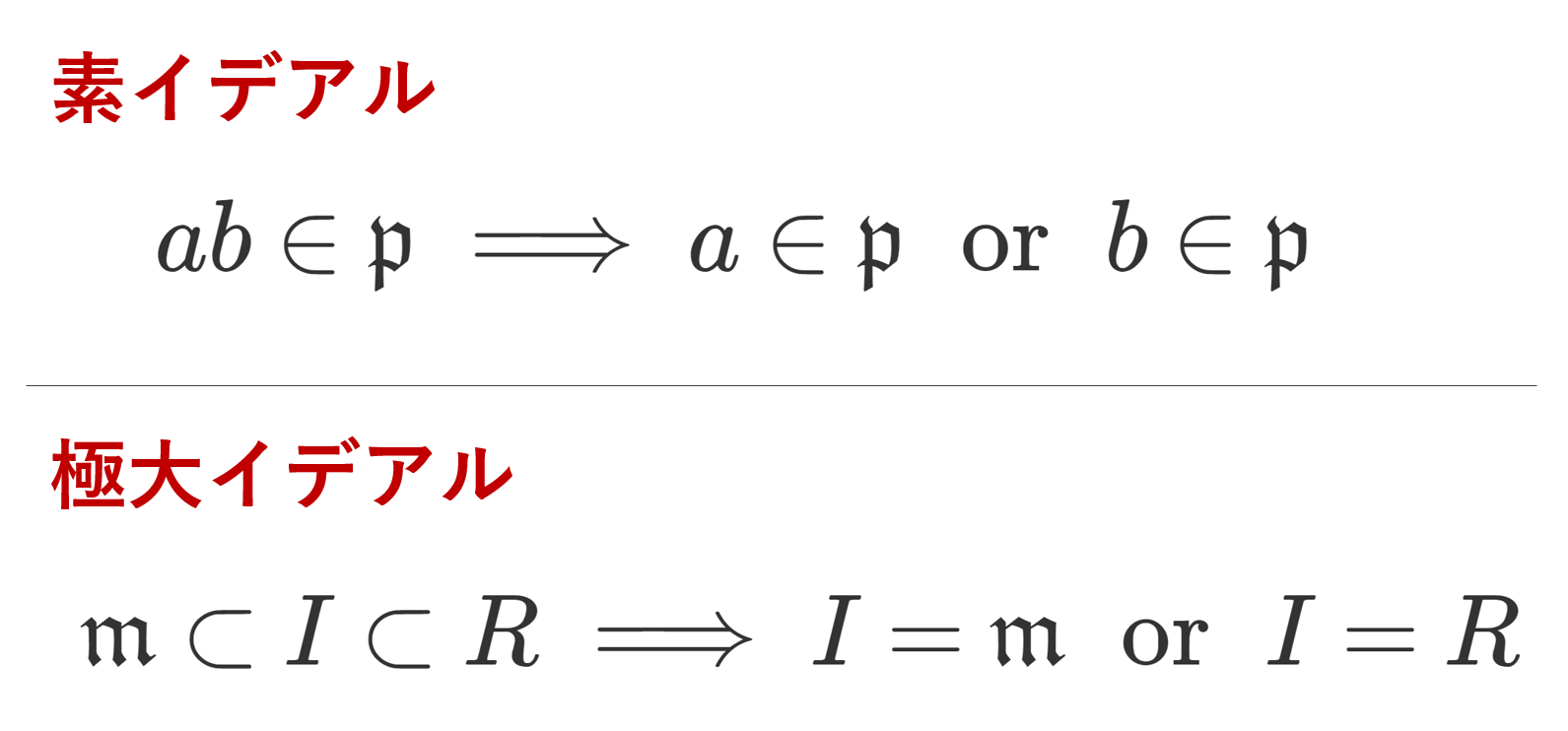可換環,特に整域における素元と既約元の概念について,その定義・具体例・性質を解説しましょう。
関連する概念として,倍元・約元・同伴の定義も紹介します。
素元と既約元
本記事で,素元・既約元は整域の上で定義することにします。整域とは, ab=0\implies a=0\text{ or } b=0 をみたす単位的な(乗法単位元をもつ)可換環です(→整域とは~定義・具体例4つ・基本的性質4つ~)。
定義(素元と既約元)
R を整域とする。
p\in R が素元 (prime element) であるとは, (p) が素イデアルであることをいう。すなわち (0)\subsetneq (p)\subsetneq R で,
\color{red} ab\in (p)\implies a\in (p)\;\text{ or } \; b\in (p)
となることをいう。
x\in R が既約元 (irreducible element) であるとは, x\ne 0 かつ x\notin R^\times かつ
\color{red}x=ab\implies a\in R^\times \;\text{ or }\; b\in R^\times
をみたすことをいう( R^\times は R の単元(可逆元)全体の集合を指す)。すなわち, x \in R\setminus (R^\times\cup \{0\}) が2つの元の積ならば,一方は単元(可逆元)である。
既約でない非零元は,可約 (reducible) という。
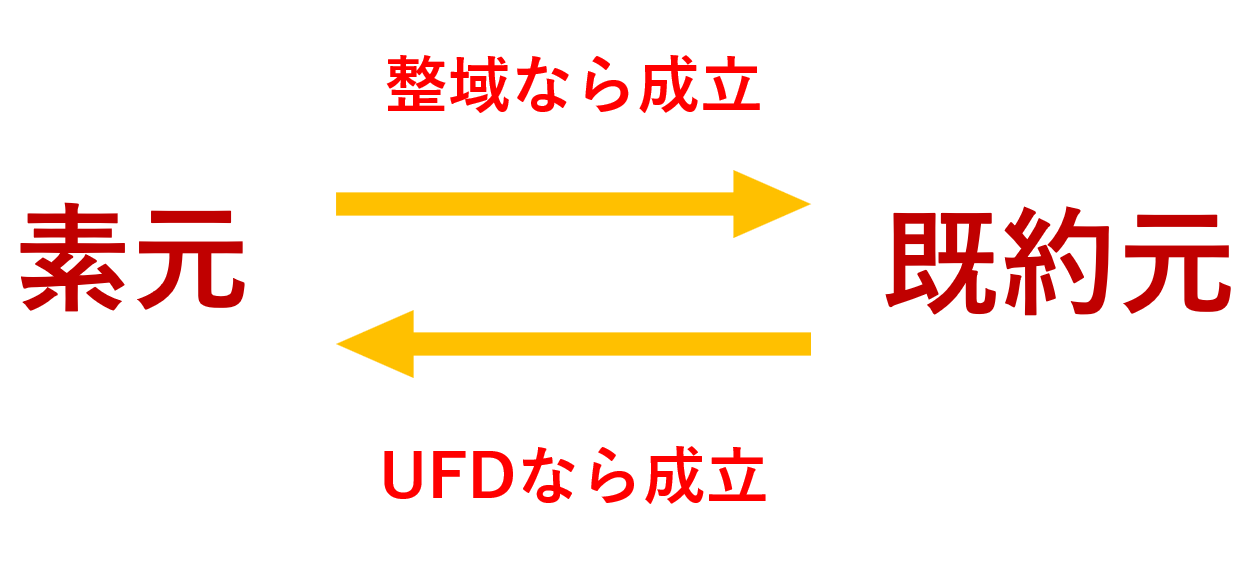
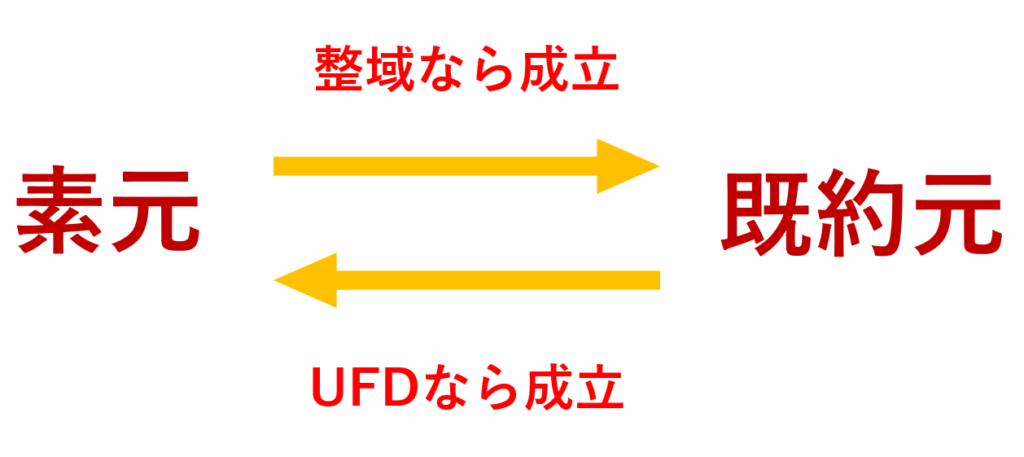
素元は素数の概念に対応しており,既約元は「これ以上割り切れない」という概念に対応しています。整数 \mathbb{Z} では,両者は同じ意味ですが,一般には違います。
まずは大事な性質を述べましょう。
素元と既約元の性質
証明
1. 素元は既約元であることについて
p\in R を素元とする。 (p) は素イデアルなので, (0)\subsetneq (p)\subsetneq R であり,特に p\ne 0,\,p\notin R^\times である。
p=ab とすると, ab\in (p) であり, (p) は素イデアルであるから, a\in (p) または b\in (p) である。同じことであるから, a\in (p) とする。すると, a=pc となる c\in R が存在する。よって,
p=ab=pcb
なので, p(1-cb)=0 である。 R は整域より, 1-cb=0 すなわち cb=1 となる。よって b\in R^\times (単元/可逆元)なので,p は既約元である。
2. 一意分解整域では,既約元は素元であることについて
p\in R を既約元とし, p=p_1p_2\dots p_n をその素元分解とする。 n \ge 1 のとき,p=p_1 は素元なので,証明が終わる。よって, n\ge 2 とする。
q=p_2\dots p_n とする。素元は既約元であることに注意して, p_2\notin R^\times である。 q\in R^\times とすると, q^{-1} が存在するが,このとき p_2^{-1}=p_3\dots p_n q^{-1} となって p_2\notin R^\times に矛盾する。よって q\notin R^\times である。
これは, p=p_2q が既約元であることに矛盾する。
証明終
素元と既約元の具体例
例1.
整数 \mathbb{Z} において,素数 p\in\mathbb{Z} は素元であり,既約元である。
素数 p に対し, (p) は素イデアルですね。すなわち, ab\in(p)\implies a \in (p)\text{ or } (b)\in (p) ( ab が p の倍数なら少なくとも一方が p の倍数)が成り立ちます。
また, p=ab ( a,b\ne \pm 1)のように分解することはできませんから,既約元でもあります。
\mathbb{Z} はユークリッド整域ですから,特に一意分解整域(UFD)です。よって素元と既約元は一致するという言い方もできますね。
例2.
k を体とする。 k 係数の多項式環 k[x] において, x\in k[x] は素元であり,既約元である。
これも定義から確認可能でしょう。 {k}[x] は一意分解整域(UFD)です。
例3.
\mathbb{Z}[\sqrt{-5}]=\{a+b\sqrt{-5}\mid a,b\in\mathbb{Z}\} において, 2 は既約元であるが,素元ではない。
2 が素元でないことは, 6=(1+\sqrt{-5})(1-\sqrt{-5})\in (2) である一方, 1\pm\sqrt{-5}\notin (2) なので, (2) は素イデアルでないです。よって分かりましたね。
2 が既約元であることを示しましょう。 2=(a+b\sqrt{-5})(c+d\sqrt{-5}) とし, a+b\sqrt{-5}, c+d\sqrt{-5} を単元(可逆元)でないとしましょう。最初の式の両辺共役を取ると, 2=(a-b\sqrt{-5})(c-d\sqrt{-5}) であり,辺々掛け合わせると
4=(a^2+5b^2)(c^2+5d^2)
です。 a+b\sqrt{-5}, c+d\sqrt{-5} は単元(可逆元)ではありませんから,とくに \pm 1 でもなく,a^2+5b^2\ne 1,\; c^2+5d^2\ne 1 です。ゆえに, a^2+5b^2=c^2+5d^2=2 です。これをみたす a,b\in\mathbb{Z} は存在しませんから,矛盾します。
以上から,2 は既約元ですね。
関連用語の定義~倍元・約元・同伴~
定義(倍元・約元・同伴)
R を整域, a,b\in R とする。
b が a の倍元 (multiple) あるいは a は b の約元 (divisor) であるとは,ある c\in R が存在して,
\large\color{red} b=ac
となることをいう。これを \color{red} a\mid b とかく。
a と b が同伴 (conjugate) であるとは,ある u\in R^\times (単元(可逆元))が存在して,
\large\color{red} b=au
と表せることをいう。
倍元・約元は,整数でいう倍数・約数を一般化したものですね。
同伴とは,単元倍を除いて同じものという意味です。 b=au なら a=bu^{-1} ですから, b が a の単元倍といっても, a が b の単元倍といっても同じことです。
また,同伴の定義は a\mid b かつ b\mid a としても構いません。実際このとき,ある c,c'\in R が存在して, b=ac,\; a=bc' とかけ,
a=bc'=acc'
ですから, a(1-cc')=0 です。 R は整域より, a=0 または cc'=1 です。 a=0 なら a= b=0 ですから良いです。 cc'=1 なら, c,c'\in R^\times ですから, a,b は同伴の定義を満たしていますね。
また,この言葉を用いると,素元 p\in R の定義は,
\color{red}p\mid ab \implies p\mid a \;\text{ or }\; p\mid b
ともかけます。 p\mid a とは a\in (p) と同じ意味ですからね。