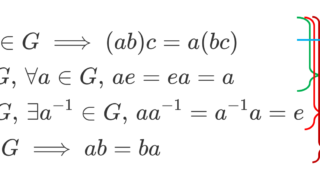乗法群,あるいは単元群とは,環や体のうち,乗法逆元の存在する元たちのなす群のことを指し, R^\times のように×で表します。乗法群について,その定義と具体例を紹介しましょう。
乗法群(単元群)の定義
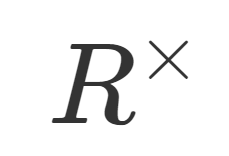
本記事では,環は単位的(乗法単位元 1 が存在)とし,零環(自明な環)でないとします。
定義(乗法群)
R を環とする。 R のうち,乗法逆元の存在する集合
R^\times = \{ a\in R\mid a^{-1} が存在 \}
は,乗法に関して群をなす。 R^\times を乗法群 (multiplicative group) または単元群 (group of units) という。
R^\times の各元を R の単元 (unit) または可逆元 (invertible element) という。
乗法に関して群になることを示しましょう。もともと群の定義は以下の通りでした。
- (ab)c=a(bc) (結合法則)
- 乗法単位元 1 が存在して,任意の a で a1=1a=a
- 任意の a に対してある a^{-1} が存在して aa^{-1}=a^{-1}a=1
そして,環はその定義から,乗法について1,2.が成り立つのでした(モノイドという)。そして,今, R^\times の元 a\in R^\times は, aa^{-1}=a^{-1}a=1 となる a\in R^\times の存在を仮定しており,さらに, a^{-1} の逆元は a という見方もできますから, a^{-1}\in R^\times もわかります。
よって, R^\times は乗法逆元に対しても閉じていて,3.が成立することが分かりますね。したがって, R^\times は積について群の定義を満たしています。
乗法群(単元群)の例
具体例を見ていきましょう。
例1.
\begin{aligned}\mathbb{Z}^\times &= \{\pm 1\},\\ \mathbb{Q}^\times &= \mathbb{Q}\setminus\{0\},\\ \mathbb{R}^\times &= \mathbb{R}\setminus \{0\},\\ \mathbb{C}^\times &= \mathbb{C}\setminus\{0\} \end{aligned}
である。
可換環 \mathbb{Q,R,C} の乗法群は単に 0 を除くだけですが, \mathbb{Z} のうち,乗法逆元が存在するものは \pm 1 だけですから,\mathbb{Z}^\times =\{\pm 1\} ですね。
例2.
K を体とするとき, K^\times = K\setminus\{0\} である。
体は「可換環かつ 0 以外のすべての元が乗法逆元を持つ」というのが定義でしたから,前半も後半も明らかですね。
例3.
\mathrm{M}_n(\mathbb{R})^\times =\mathrm{GL}_n(\mathbb{R}) である。ただし, \mathrm{M}_n(\mathbb{R}) は 実数を成分とする n 次正方行列のなす行列環で, \mathrm{GL}_n(\mathbb{R})=\{ A\in\mathrm{M}_n(\mathbb{R})\mid \det A\ne 0\} は正則行列(可逆行列)のなす一般線形群である。
非可換環における乗法群の例ですね。
例4.
n\ge 2 を整数とする。
|(\mathbb{Z}/n\mathbb{Z})^\times |=\phi(n) である。ただし,右辺はオイラー関数であり, 1,2,\dots, n のうち,n と互いに素なものの個数を表す。
\mathbb{Z}/n\mathbb{Z} は{}\bmod n の世界ですね。 {}\bmod n において,乗法逆元が存在するのは,n と互いに素な整数のときです。よって, (\mathbb{Z}/n\mathbb{Z})^\times とは, 1,2,\dots, n のうち,n と互いに素な整数たちが積によってなす群です。
例5.
R を整域とするとき, R[x]^\times = R^\times である。
整域とは,0 以外に零因子を持たない可換環です(→整域とは~定義・具体例4つ・基本的性質4つ~)。 R[x] とは R 係数多項式環です。
整域ならば, a,b\ne 0\implies ab\ne 0 であり,これを用いると,多項式の次数について, \operatorname{deg}(f(x)g(x))=\operatorname{deg} f(x)+ \operatorname{deg} g(x) が成り立ちます。すると, f(x)g(x)=1 とすると,\operatorname{deg} f(x)=\operatorname{deg} g(x)=0 となって, f(x),g(x)\in R となりますから,例5.の等式が成立するわけです。
例6.
R,S を環とし, f\colon R\to S を環準同型とする。このとき, f(R^\times) \subset S^\times であり, 群準同型写像 f\colon R^\times \to S^\times を引き起こす。
いったん f(R^\times)\subset S^\times を認めれば,環準同型写像の定義を考えれば, f\colon R^\times \to S^\times が群準同型になるのはわかりますね。 よって f(R^\times)\subset S^\times のみ示しましょう。
a\in R^\times とすると,f(a)f(a^{-1})=f(aa^{-1})=f(1)=1=f(1)=f(aa^{-1})=f(a)f(a^{-1}) ですから, f(a^{-1})=f(a)^{-1} であり, f(a)\in S^\times ですね。よって f(R^\times)\subset S^\times です。