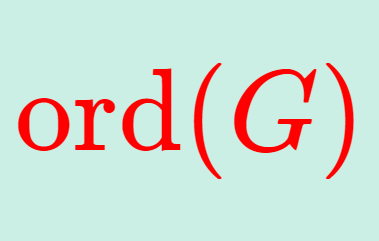群の位数・元の位数について,その定義・具体例・性質を順番に解説しましょう。
群の位数・元の位数とは
「群の位数」と「元の位数」は言葉の意味が違います。これについて,定義と具体例をしっかり確認していきましょう。
群の位数・元の位数の定義
定義(群の位数・元の位数)
G を群とする。
- G の元の個数を群 G の位数 (order) という。
- g\in G に対して, g^n = e (単位元)となる最小の正の整数 n を元 g の位数 (order) という。そのような正の整数が存在しないときは,元 g の位数は \infty と約束する。
群 G の位数は \color{red} |G|, \operatorname{ord}(G) などと表され,元 g の位数は \color{red} |g|, \operatorname{ord}(g) などと表されることがある。
群 G の位数とは,単に G を集合と見たときの元の個数すなわち濃度を指します。一方,元 g の位数とは,何回かけ合わせて単位元 e に戻ってくるかを表しています。
なお,位数が有限の群を有限群 (finite group),位数が無限の群を無限群 (infinite group) といいます。
群の位数・元の位数の具体例
例1( \mathbb{Z}).
加法(和)に関する群 \mathbb{Z} の位数は \infty であり,元 2\in\mathbb{Z} の位数は \infty である。
\mathbb{Z} が元の数が無限個ある集合ですから位数は \infty であり, 2\in\mathbb{Z} は何回足しても単位元 0 にならないので,元 2 の位数は \infty ですね。
例2( {}\bmod 10).
{}\bmod 10 における加法(和)に関する群 \mathbb{Z}/10\mathbb{Z} の位数は 10 であり,元 1 \in \mathbb{Z}/10\mathbb{Z} の位数は 10 である。また,元 2\in \mathbb{Z}/10\mathbb{Z} の位数は 5 である。
{}\bmod 10 の世界の元は 0,1,2,\dots, 9 と思えるので, | \mathbb{Z}/10\mathbb{Z} | =10 であり,元 1 は 10 回足すと単位元 0 に戻るので,元 1 の位数は 10 です。一方で, 2 は 5 回足しただけで 0 になるので,位数は 5 です。
例3(対称群).
置換 \sigma\colon \{1,2,3\}\to \{1,2,3\} 全体が写像の合成に関してなす群(対称群) S_3 について,
群 S_3 の位数は 3!=6 であり,互換 (12)\in S_3 の位数は 2 であり,巡回置換 (123)\in S_3 の位数は 3 である。
互換 (12) は, 1,2 を入れ替える置換で,巡回置換 (123) は 1 を 2 に, 2 を 3 に, 3 を 1 に入れ替える置換です。
(12) は 2 回合成すると元に戻り(恒等写像になり), (123) は 3 回合成すると元に戻るので,それぞれ位数は 2,3 です。ちなみに S_3 に位数 6 の元は存在しません。
群の位数・元の位数の性質
最後に,群の位数と元の位数の性質を述べましょう。
定理(群の位数・元の位数の性質)
G を群とする。
- 元 g\in G の位数が 1 である必要十分条件は g=e (単位元) である。
- G の位数を n<\infty とすると,各元 g\in G の位数は n の約数である。
1. は明らかでしょう。2.の証明には,ラグランジュの定理を用います(→ラグランジュの定理とその証明・応用例【群論】)。
ここでは,群 G の位数が有限であれば元 g\in G の位数も有限であることだけ示しておきましょう。
群の位数が有限ならば元の位数も有限である証明
群 G の位数は有限であるから,g,g^2,g^3, \dots \in G のなかに同じものが存在する(部屋割り論法)。
g^m = g^n \; (m<n ) とすると,両辺 g^{-m} をかけて e = g^{n-m}. したがって,元 g の位数は n-m 以下である。
証明終