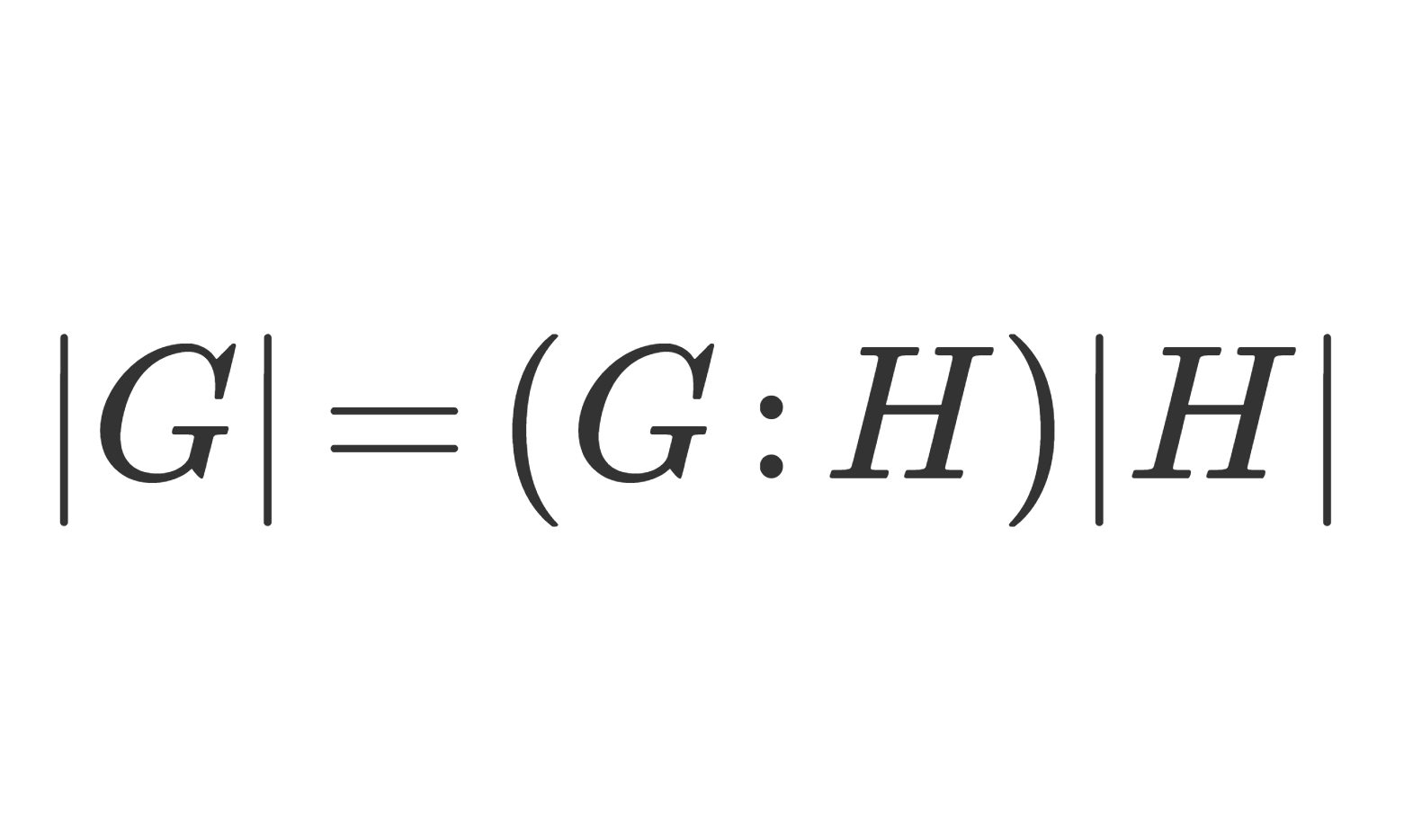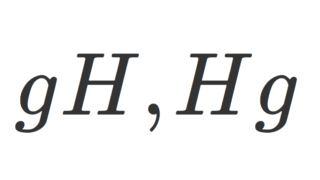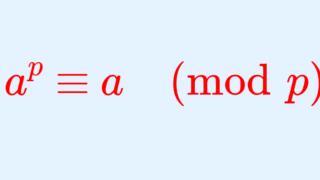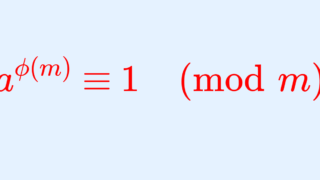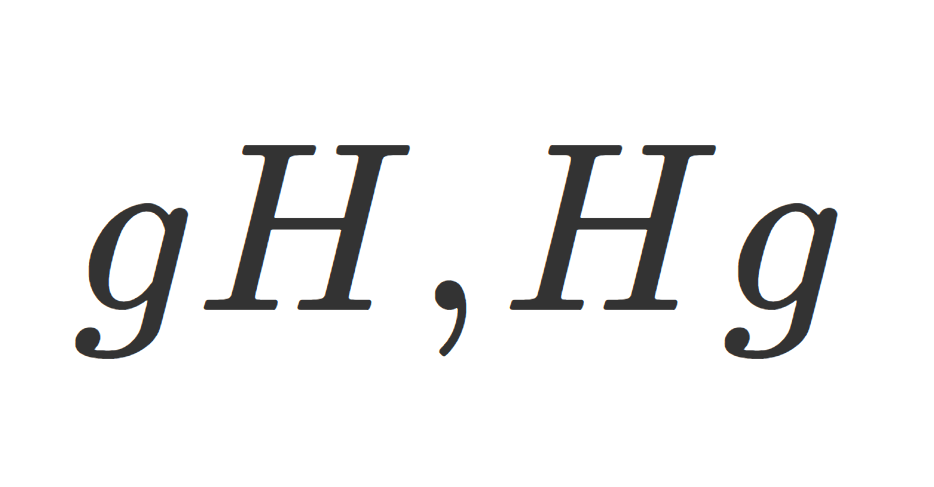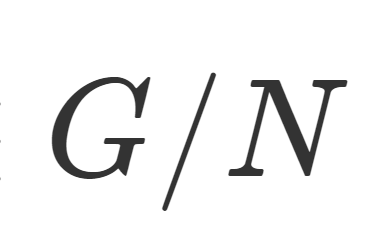ラグランジュの定理とは,有限群とその部分群の位数における基本的な定理で,有限群の分類などに非常に役に立つ定理です。
ラグランジュの定理について紹介・証明し,応用例も挙げましょう。
ラグランジュの定理
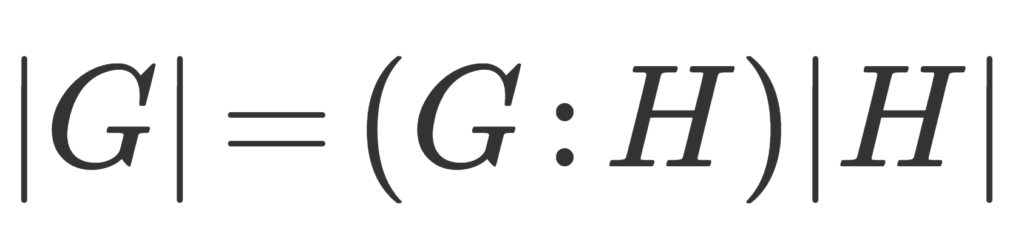
ちょっと忘れてる言葉が出てくるかもしれませんが,あとで復習を入れるので,全くの初見でなければ各リンク先には飛ばなくてよいです。
「有限群」とは,集合として有限集合である群のことです。
ラグランジュの定理 (Lagrange’s theorem)
G を有限群とし, H\subset G をその部分群とする。このとき,
本記事では, (G:H) は部分群 H\subset G の指数 (index) を表すことにします(後で軽く復習します)。
復習ですが,群 G の位数 (order) とは,集合としての要素の個数を表します。元 g\in G の位数 (order) とは, g^n=e (単位元)となる最小の n\ge 1 のことで,巡回群 \langle g\rangle の位数に一致します(→群の位数・元の位数とは~定義・例・性質~)。
1.が示せれば2.は明らかです。元 g\in G の位数は部分群 \langle g\rangle \subset G の位数ですから,1.から直ちに従うからです。
ラグランジュの定理の証明
証明の準備
証明のために必要である,
- 左剰余類
- 左剰余集合と指数
について復習しておきましょう。
右剰余類も同様に定義できますが,今回はなくてもいいので省略します。
左剰余類全体の集合 \color{red} G/H =\{gH\mid g\in G\} を左剰余集合 (left factor set) という。
左剰余集合の濃度(要素の個数)を部分群 H\subset G の指数 (index) といい,\color{red} (G:H) や [G:H] などとかく。
以上,必要な概念を軽く復習しました。以上の概念の詳しい解説は以下の記事で行っています。
ラグランジュの定理の証明
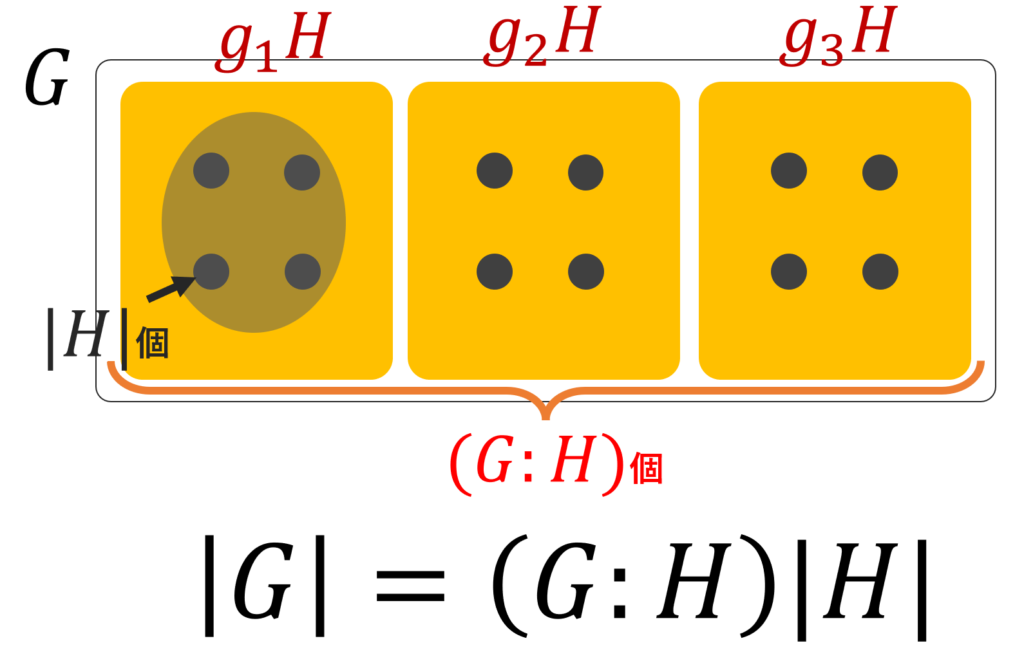
さて,証明にうつりましょう。証明すべきはラグランジュの定理1.の |G| = (G:H)|H| です。
証明
左剰余類について (1) 式より, G の各元は G/H=\{ gH\mid g\in G\} 内のいずれか一つのみの左剰余類に属する。(これは「左剰余類が同値類だから」と言ってもよい。)
よって群 G の位数は,各左剰余類の濃度(元の個数)を全て足し合わせたものである。
(2) 式より,各左剰余類の濃度は |H| に等しい。 G/H の濃度,すなわち左剰余類の個数は (G:H) 個なので, |G| = (G:H)|H| となる。
証明終
ラグランジュの定理の応用例
ラグランジュの定理の簡単な応用例を挙げましょう。
例1.
位数 15 の群は,位数 4 の部分群を持ち得ない。
4 は 15 の約数ではないからですね。
例2.
素数位数の群 G は巡回群である。
元 e\ne g\in G の位数は,素数の約数ですからその素数自身になり, G=\langle g\rangle となるからですね。これについては,以下でも解説しています。
他にも,ラグランジュの定理の応用として有名なのは,フェルマーの小定理や,それを一般化したオイラーの定理の証明に利用することです。以下で解説しています。