 解析学(大学)その他
解析学(大学)その他 区間縮小法の原理とその証明~実数の連続性~
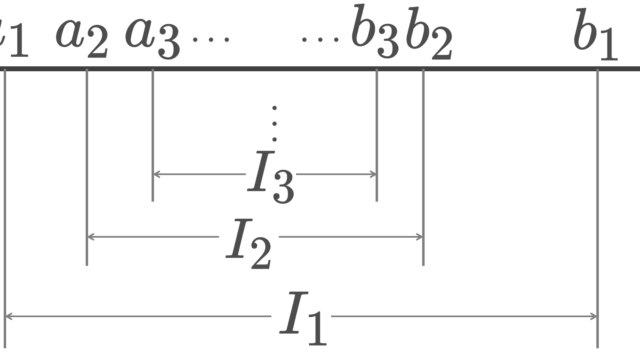
区間縮小法の原理とは,単調減少な閉区間の列の幅が0に収束するならば,閉区間は最後は1点に収束するという定理です。区間縮小法の原理は,実数の連続性が深く関係しています。区間縮小法の原理について,実数の連続性を認めて証明し,逆に区間縮小法の原理から実数の連続性を導くこともできるため,それも紹介します。
 解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他 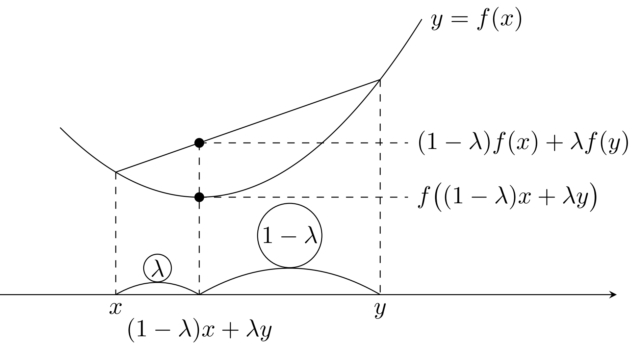 解析学(大学)その他
解析学(大学)その他 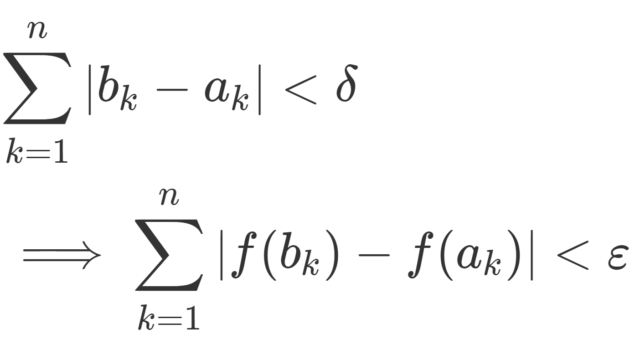 解析学(大学)その他
解析学(大学)その他 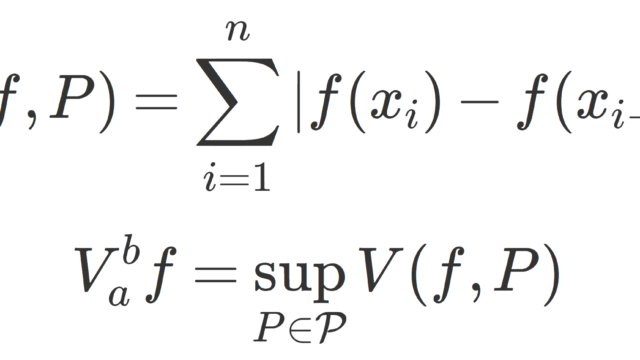 解析学(大学)その他
解析学(大学)その他 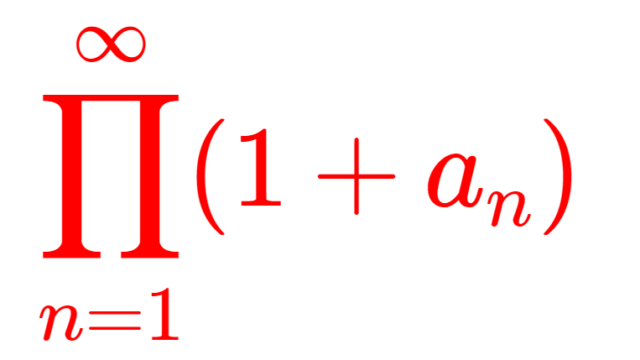 解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他  解析学(大学)その他
解析学(大学)その他