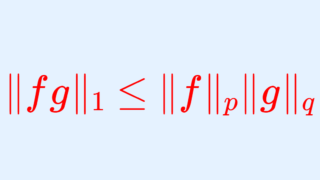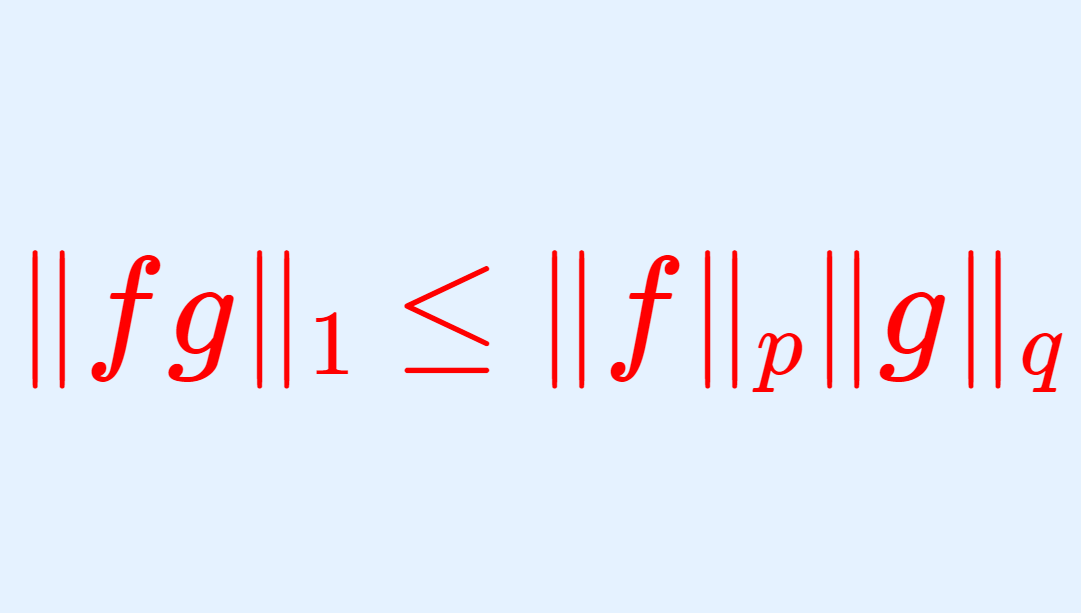ヤングの不等式とは,任意の a,b\ge 0 と 1/p+1/q=1 をみたす p,q>1 に対し,
ab\le \frac{a^p}{p} +\frac{b^q}{q}
という不等式のことを言います。これについて,証明とその発展形を紹介しましょう。
ヤングの不等式とは
定理(ヤングの不等式; Young’s inequality)
a,b\ge 0,\; p,q>1 かつ 1/p+1/q=1 とする。このとき,
\color{red} \large ab\le \frac{a^p}{p} +\frac{b^q}{q}
であり,等号成立は a^p=b^q のとき。
ヤングの不等式は,相加相乗平均の不等式の一般化になっています。実際, p=q=1/2 とすると,
ab\le \frac{a^2}{2}+\frac{b^2}{2}
ですね。
ヤングの不等式を証明しましょう。もっとも一般的なのは,凸関数の議論を用いることです。
証明
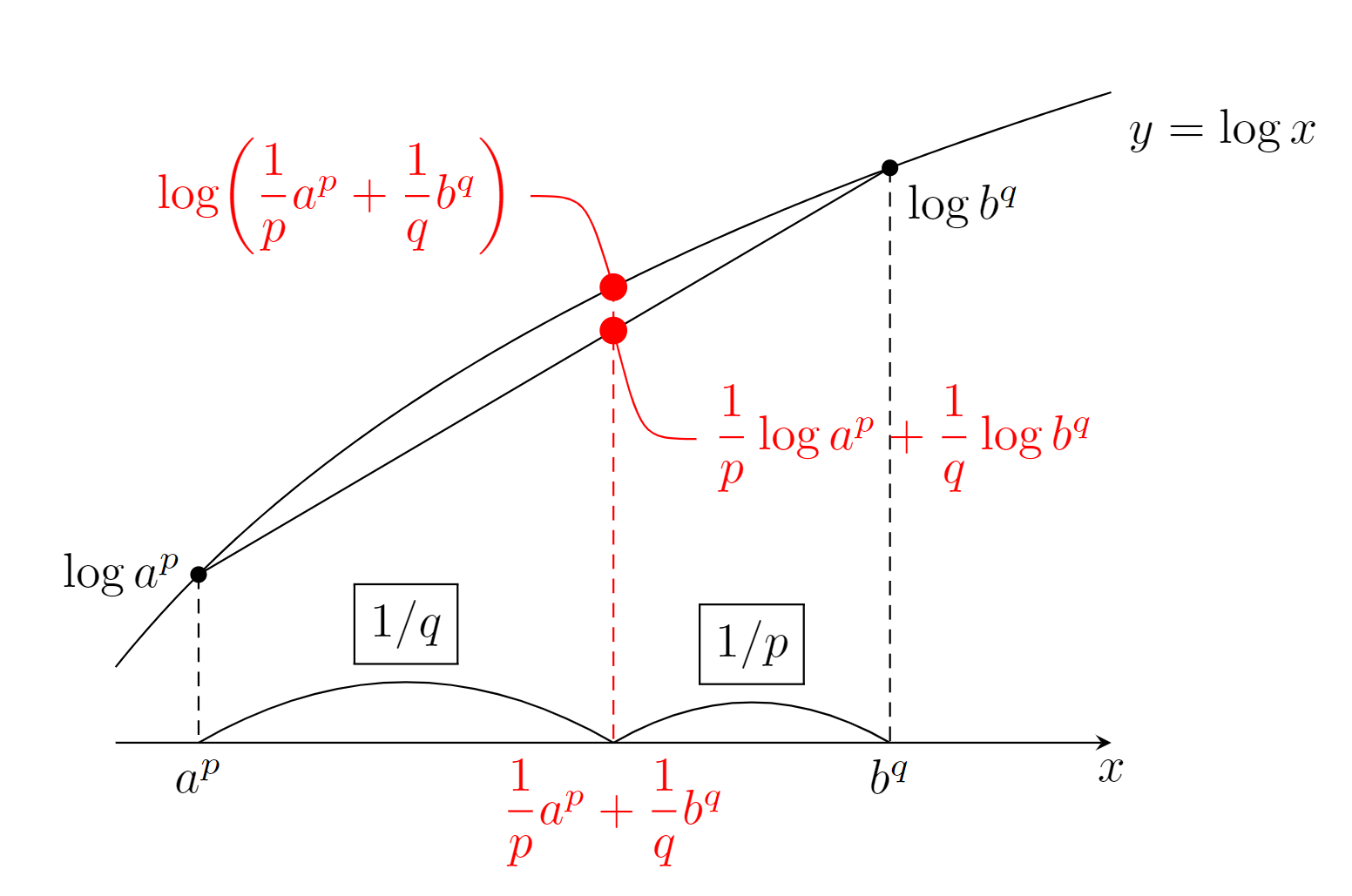
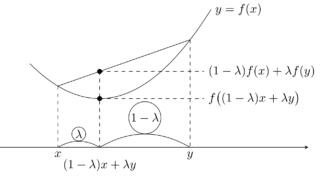
a=0 または b=0 のときは明らかなので,a,b>0 としてよい。 x\mapsto \log x は凹関数( -\log が凸関数)なのと, 1/p+1/q=1 より,
\begin{aligned}\log ab =\log a+\log b&=\frac{1}{p} \log a^p +\frac{1}{q}\log b^q \\&\le \log\left(\frac{a^p}{p}+\frac{b^q}{q}\right)\end{aligned}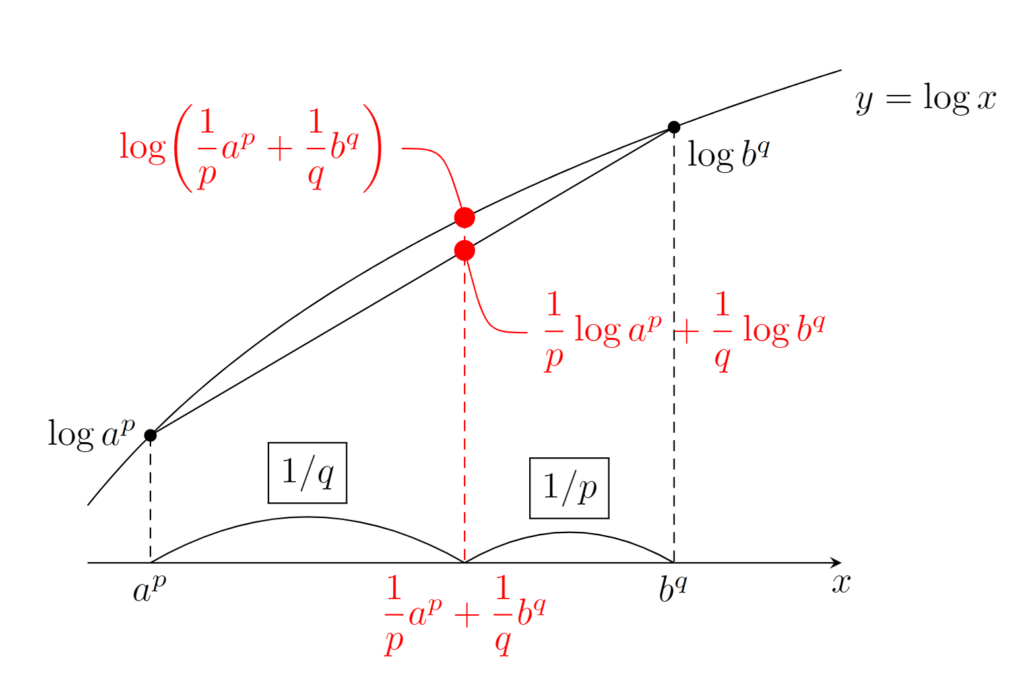
である(上は a^p<b^q のときの図)。特に, x\mapsto \log x は狭義凸なので,等号成立は a^p=b^q のときである。両端辺を比較することで,
を得る。
証明終
ヤングの不等式の一般化
定理(積分型のヤングの不等式)
f\colon [0,c] \to [0,f(c)] を f(0)=0 をみたす狭義単調増加な連続関数とする。このとき, 0\le a\le c ,\; 0\le b\le f(c) に対し,
\color{red} ab\le \int_0^a f(x)\,dx +\int_0^b f^{-1}(x)\,dxこれの証明は,下の図を見れば一発で分かるでしょう。
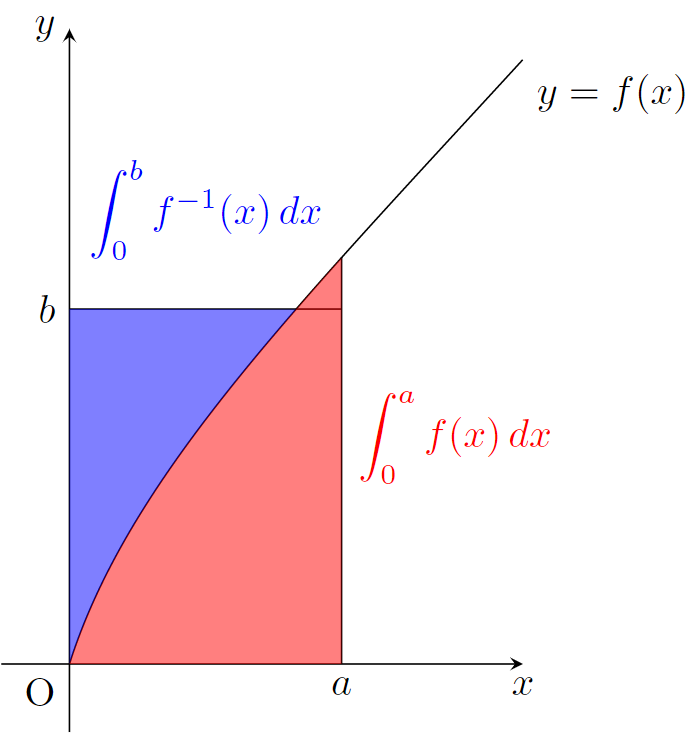
この式に, f(x)=x^{p-1} を入れると,
\begin{aligned}ab&\le \int_0^a x^{p-1}\,dx +\int_0^b x^{1/(p-1)}\,dx \\ &= \left[\frac{1}{p} x^p\right]_0^a + \left[ \frac{p-1}{p} x^{p/(p-1)} \right]_0^b \\ &= \left[\frac{1}{p} x^p\right]_0^a + \left[ \frac{1}{q} x^{q} \right]_0^b \\ &=\frac{a^p}{p} +\frac{b^q}{q} \end{aligned}
ですから,前半のヤングの不等式の一般化になっていますね。
ヤングの不等式は,解析学においてヘルダーの不等式など,別の不等式の証明に使われます。ヘルダーの不等式は以下で解説しています。