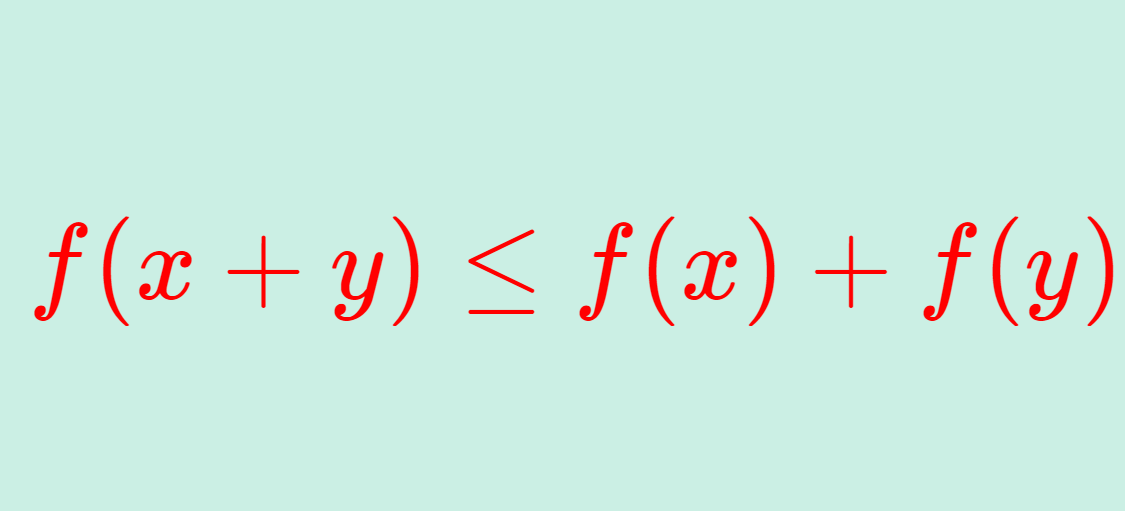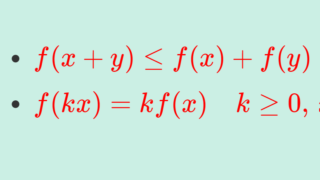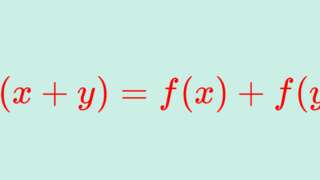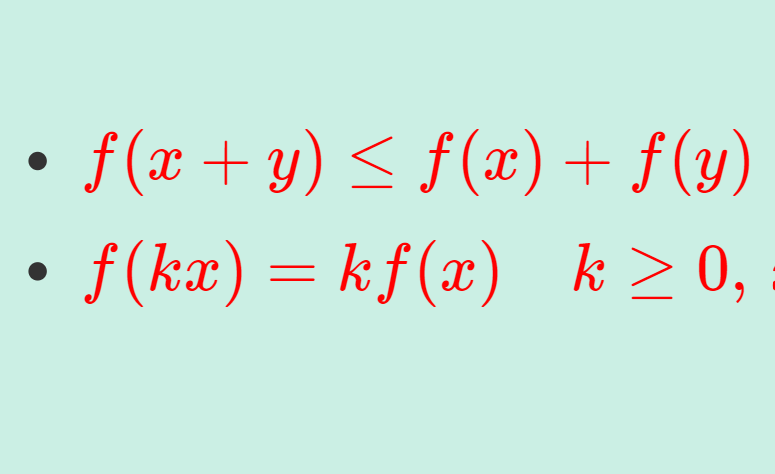劣加法性を持つ関数の定義と性質

劣加法的関数 (subadditive function) の定義とその性質について解説します。

劣加法的関数・優加法的関数の定義
1. 劣加法的関数
2. 優加法的関数
劣加法的関数の具体例
劣加法的関数の性質
補足
参考文献

劣加法的関数・優加法的関数の定義

劣加法的関数

定義（劣加法的関数）

$I \subset \mathbb{R}$ を， $x,y \in I \Rightarrow x+y \in I$ となる集合 (cone) とする。
関数 $f \colon I \to \mathbb{R}$ が

\textcolor{red}{f(x+y) \le f(x) + f(y), \quad x,y \in I}

をみたすとき，劣加法的 (subadditive) であるという。

なお，関数の定義域は $C \subset \mathbb{R}^n$ とすることもあります。
終域は $[-\infty, \infty]$ とすることもあります。

優加法的関数

逆の不等式が成り立つ「優加法的関数」というのもありますから，定義しておきましょう。

定義（優加法的関数）

$I \subset \mathbb{R}$ を， $x,y \in I \Rightarrow x+y \in I$ となる集合 (cone) とする。
関数 $f \colon I \to \mathbb{R}$ が

\textcolor{red}{f(x+y) \ge f(x) + f(y), \quad x,y \in I}

をみたすとき，優加法的 (superadditive) であるという。

ここで， $f$ が優加法的 $\Longleftrightarrow$ $-f$ が劣加法的ですから，劣加法的関数の性質のみ考えれば，優加法的関数の性質もわかると言えます。従って，以下は劣加法的関数のみ扱います。

劣加法的関数の具体例

具体例を挙げましょう。

具体例

以下の関数 $f\colon \mathbb{R} \to \mathbb{R}$ は劣加法的である。

$\textcolor{red}{f(x) = |x|^\alpha, \quad 0 < \alpha \le 1 }.$
$\textcolor{red}{f(x) = \begin{cases} \log(x+1) & x \ge 0, \\ 0 & x < 0.\end{cases}}$
$\textcolor{red}{f(x) = \begin{cases} 0 & x \in \mathbb{Q}, \\ 1 & x \in \mathbb{R}\setminus \mathbb{Q}.\end{cases}}$ (ディリクレ関数のある意味「逆」)

劣加法的関数の性質

劣加法的関数の基本的な性質

定理（劣加法的関数の基本的な性質）

$f, g$ を劣加法的とするとき， $a, b \ge 0$ に対して $af+bg$ も劣加法的である。
$\{f_n\}$ を劣加法的関数の列とし， $f(x) = \lim_{n\to\infty} f_n(x)$ が有限値であるとすると， $f$ は劣加法的である。
f\colon \mathbb{R} \to \mathbb{R} を劣加法的とすると，
1. $f(0) \ge 0.$
2. $f(-x) \ge -f(x).$
3. $f$ が偶関数ならば $f(x) \ge 0.$
4. $f$ が奇関数ならば $f(x+y) = f(x) + f(y)$ ，すなわち $f$ は加法的 (additive)。

略証

1. 明らか，2. 明らか。

3-1. $f(0) \le f(0)+f(0)$ より。
3-2. $0 \le f(0) \le f(x) + f(-x)$ より。
3-3. $f(x) = f(-x) \ge -f(x)$ より。
3-4. $f(x) \le f(x+y) + f(-y) = f(x+y) - f(y)$ を移項して， $f(x) + f(y) \le f(x+y)$ より。

略称終

なお，これらは全て $f\colon \mathbb{R}^n \to \mathbb{R}$ として成立します。

劣加法的関数の極限挙動

以下の定理は面白いので証明したいと思います。

定理（極限挙動）

$f\colon (0, \infty) \to \mathbb{R}$ は劣加法的で，任意の有界閉区間で有界であるとする。
このとき， $\lim_{x\to\infty} f(x) / x$ が存在して，

\lim_{x\to\infty} \frac{f(x)}{x} = \inf_{x>0} \frac{f(x)}{x}

となる。

なお「任意の有界閉区間で有界」は，「可測関数である」または「ある有界閉区間で有界」であれば従うことが知られています。

証明

$\alpha = \inf_{x>0} f(x) /x \in [-\infty, \infty)$ とおく。 $\alpha = -\infty$ のときは明らかなので， $\alpha > - \infty$ とする。このとき， $\varepsilon > 0$ として， $f(a) / a < \alpha + \varepsilon$ となる $a > 0$ を一つとる。

$n_x = \lfloor x/a \rfloor - 2$ と定める(ただし， $\lfloor\cdot \rfloor$ は床関数(ガウス記号))。このとき，

\begin{aligned} f(x) &\le f(n_x a) + f(x - n_x a) \\ &\le n_x f(a) + f(x-n_x a) \\ &\le n_x f(a) + M \end{aligned}

である。ここで， $M = \sup_{x \in [2a,3a]} f(x)$ とした。よって，

\begin{aligned} \alpha &\le \frac{f(x)}{x} \\ &\le \frac{n_x a}{x} \frac{f(a)}{a} + \frac{M}{x} \\ &\le \frac{n_x a}{x} (\alpha + \varepsilon) + \frac{M}{x} \\ &\xrightarrow{x\to\infty} \alpha + \varepsilon \end{aligned}

となるから，結論が従う。

証明終

また，逆に以下も知られています。

定理

関数 $f\colon (0, \infty) \to \mathbb{R}$ に対し， $f(x) / x$ が単調減少となるとき， $f$ は劣加法的である。

証明

$x, y \in (0, \infty)$ に対し，

\begin{aligned} f(x+y) &= x \frac{f(x+y)}{x+y} + y \frac{f(x+y)}{x+y} \\ &\le x \frac{f(x)}{x} + y \frac{f(y)}{y} \\ & = f(x) + f(y) \end{aligned}

より。

証明終

劣加法的関数の連続性

次に連続性の定理を挙げます。

定理（連続性）

$f\colon \mathbb{R}^n \to \mathbb{R}$ が劣加法的で， $f(0) = 0$ かつ $f$ が $0$ で連続ならば， $f$ は全体で連続である。

証明

$x, \delta \in \mathbb{R}^n$ とする。このとき，劣加法的であることから，
$\begin{gathered} f(x+\delta) - f(x) \le f(\delta), \\ f(x) - f(x+\delta) \le f(-\delta) \end{gathered}$

なので，