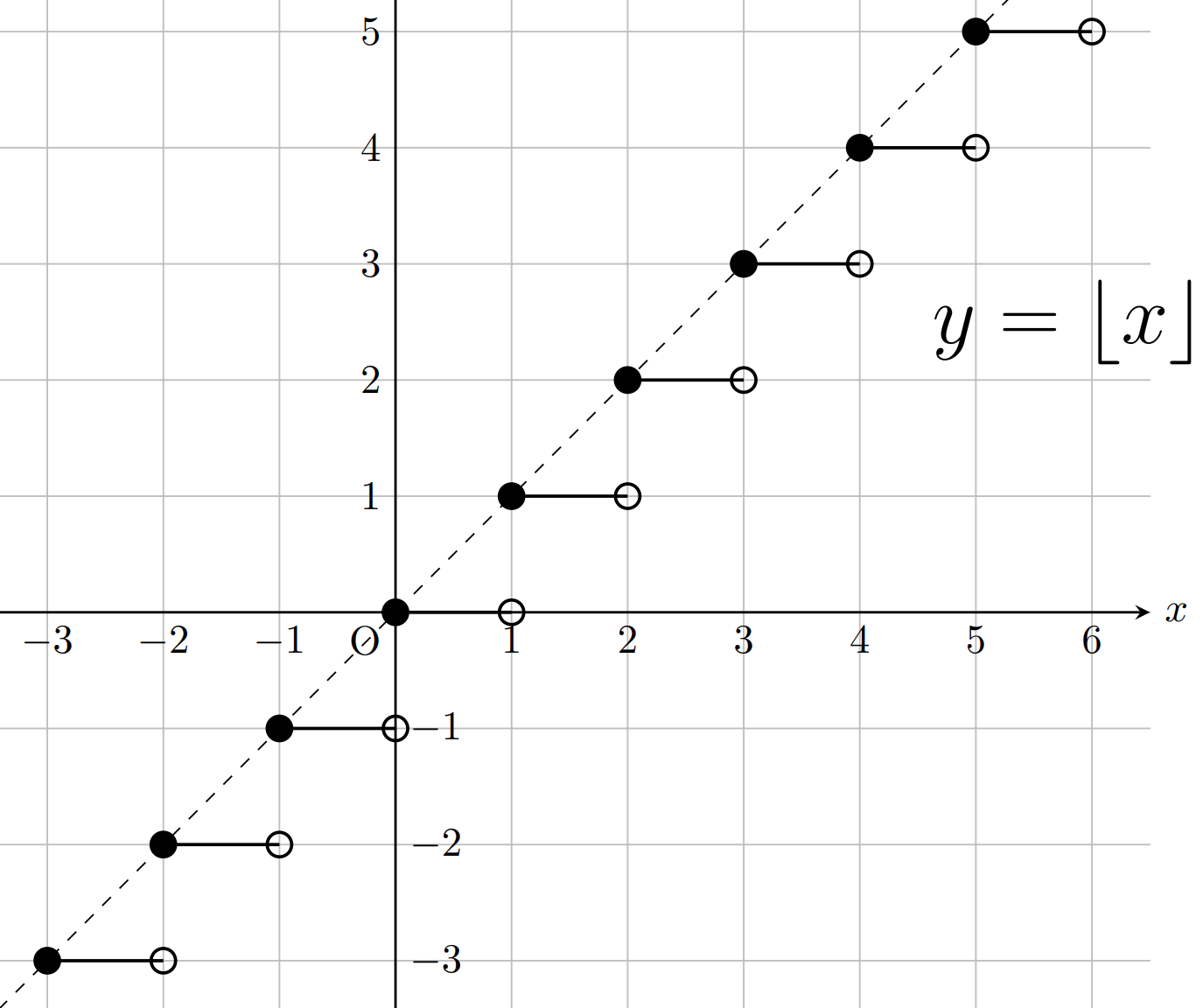
床関数・天井関数といったり,高校ではガウス記号とも呼んだりする関数の定義やそのグラフ・性質について解説します。
床関数(ガウス記号)・天井関数の定義と具体例
まずは定義・具体例を述べましょう。
床関数(ガウス記号)・天井関数の定義
定義(床関数(ガウス記号)・天井関数)
x \in \mathbb{R} に対して, x を超えない最大の整数 \color{red}\lfloor x \rfloor を返す関数
\color{red} \lfloor \cdot \rfloor \colon \mathbb{R} \to \mathbb{Z}
を床関数 (floor function) という。床関数は \lfloor x \rfloor 以外にも \color{red} [ x ] とも表されることが多い。このときの \color{red} [ \cdot ] をガウス記号ともいう。
逆に, x 未満でない最小の整数 \color{red} \lceil x \rceil を返す関数
\color{red} \lceil \cdot \rceil \colon \mathbb{R} \to \mathbb{Z}
を天井関数 (ceiling function)という。
「 x を超えない最大の整数」や「 x 未満でない最小の整数」というのは,少しわかりにくいかもしれません。同値な表現を与えましょう。
- \lfloor x \rfloor は, x を超えない最大の整数
- \lfloor x \rfloor は, x の整数部分(この定義は注意が必要)
- \lfloor x \rfloor は, x の小数点以下を切り捨てたものである
- \lfloor x \rfloor = \max\{ n \in \mathbb{Z} \mid n \le x \}
- \lfloor x \rfloor は, n \le x < n+1 となる整数 n
- \lceil x \rceil は, x 未満でない最小の整数
- \lceil x \rceil = \min\{ n \in \mathbb{Z} \mid x \le n \}
- \lceil x \rceil は, x の小数点以下を切り上げたものである
- \lceil x \rceil は, n-1 < x \le n となる整数 n
「 \lfloor x \rfloor は x の整数部分」というのは分かりやすい表現ですが,少しばかり注意が必要です。以下の具体例を見てください。
床関数(ガウス記号)・天井関数の具体例
床関数・天井関数の具体例
- \displaystyle \lfloor 2 \rfloor = 2.
- \displaystyle \lfloor 3.6 \rfloor = 3.
- \displaystyle \lfloor \pi \rfloor = 3.
- \displaystyle \lfloor -4 \rfloor = -4.
- \displaystyle \lfloor -7.3\rfloor = -8.
- \displaystyle \lceil 2 \rceil = 2.
- \displaystyle \lceil 3.4 \rceil = 4.
- \displaystyle \lceil 2\pi \rceil = 7.
- \displaystyle \lceil -2 \rceil = -2.
- \displaystyle \lceil -5.05 \rceil = -5.
5.を見てください。 \lfloor x \rfloor は x の整数部分と思うことにすると, -7.3 の整数部分は -7 でなく, -8 になることに注意しましょう。
加えて, x - \lfloor x \rfloor を x の小数部分とすると, -7.3 の小数部分は -0.3 でなく, 0.7 になります。
床関数(ガウス記号)・天井関数のグラフのイメージ
床関数・天井関数のグラフを描画してみましょう。
まずは床関数です。点線は y= x のグラフを表します。
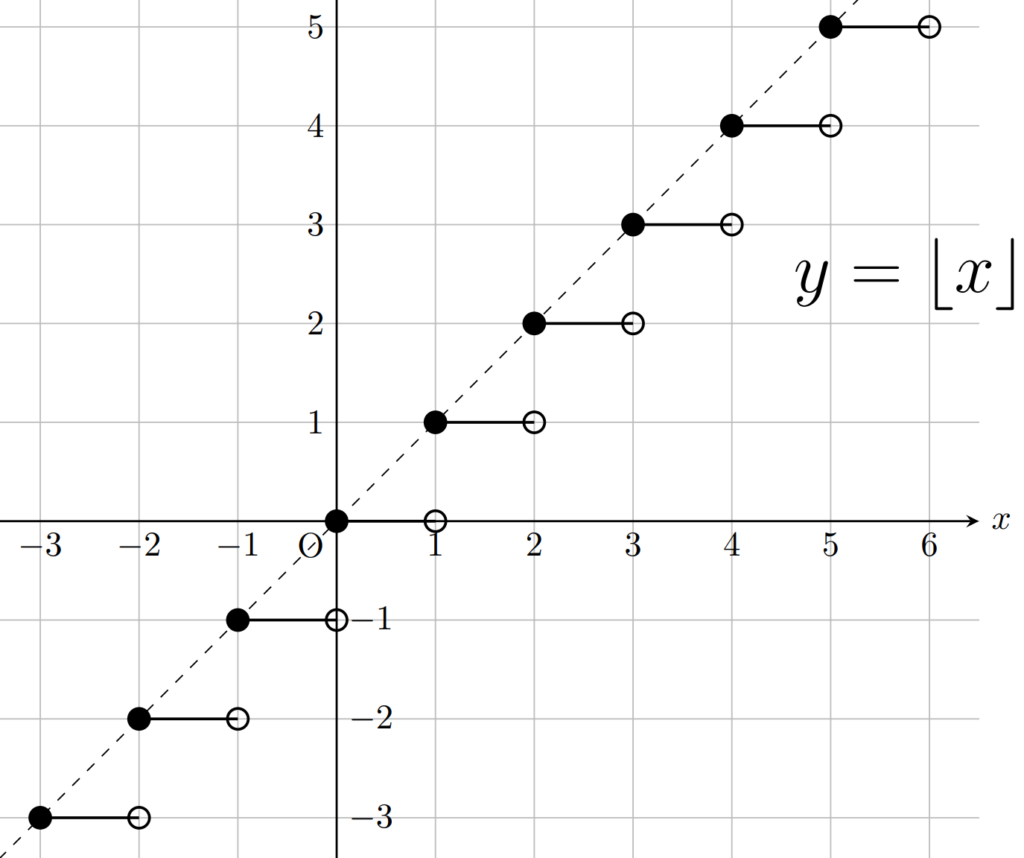
\lfloor x \rfloor \le x なので, y = x のグラフよりも下になります。また,この関数は右連続です。
続いて天井関数も描画しましょう。同じく点線は y= x のグラフを表します。
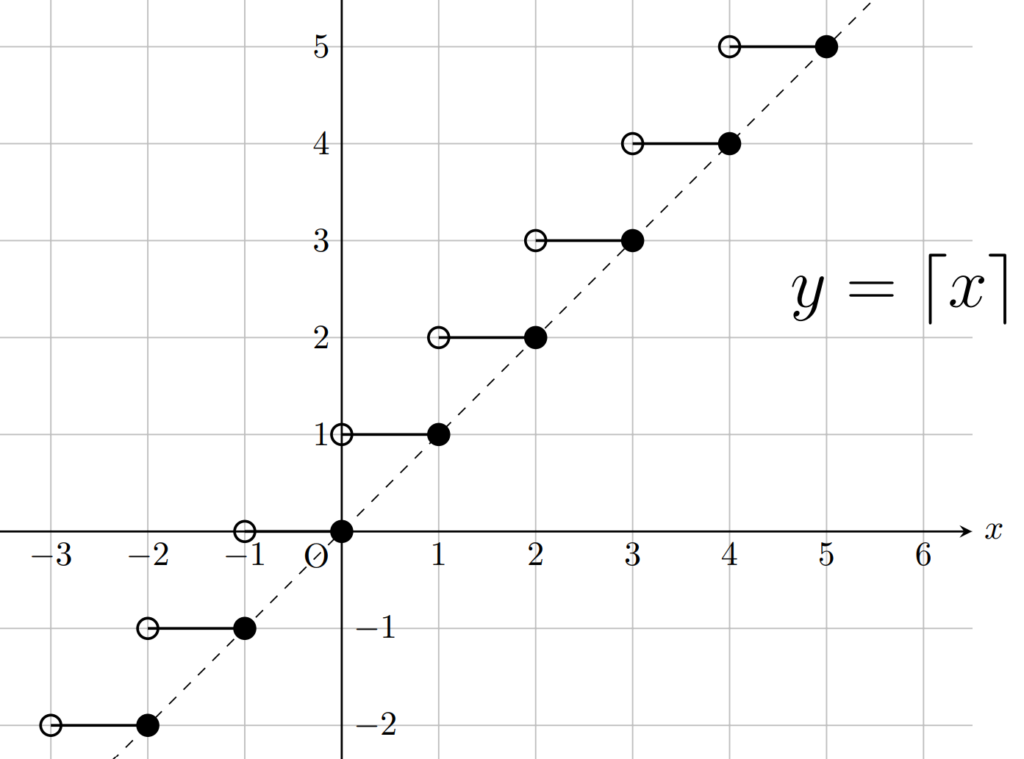
\lceil x \rceil \ge x なので, y = x のグラフよりも上になります。また,この関数は左連続ですね。
床関数(ガウス記号)・天井関数の性質
床関数・天井関数には以下の性質があります。
定理(床関数・天井関数の性質)
以下, x, y, z \in \mathbb{R} \, , n \in \mathbb{Z}, \, r \in \mathbb{R}\setminus \mathbb{Z}, \, a ,b> 0 とする。このとき,
- \lfloor x\rfloor \le x < \lfloor x \rfloor +1 .
- \lceil x \rceil - 1 < x \le \lceil x \rceil .
- x-1<\lfloor x \rfloor \le x.
- x \le \lceil x \rceil < x+1.
- \lfloor n \rfloor = n = \lceil n \rceil .
- \lfloor r \rfloor < r < \lceil r \rceil = \lfloor r \rfloor + 1 .
- \lfloor x+y \rfloor \ge \lfloor x \rfloor + \lfloor y \rfloor.
- \lceil x + y \rceil \le \lceil x \rceil + \lceil y \rceil.
- \lfloor ab \rfloor \ge \lfloor a \rfloor \lfloor b \rfloor.
- \lceil ab \rceil \le \lceil a \rceil \lceil b \rceil.
- \lfloor x + n \rfloor = \lfloor x \rfloor + n.
- \lceil x + n \rceil = \lceil x \rceil + n.
- \lfloor nx \rfloor = \sum_{k=0}^{n-1} \lfloor x + k/n \rfloor (エルミート等式; Hermite’s identity)
- \lceil nx \rceil = \sum_{k=0}^{n-1} \lceil x - k/n \rceil .
全て定義から丁寧に考えれば難しくありませんが,最後の2つだけ証明してみましょう。
13-14. の証明
p + q/n \le x < p + (q+1)/n となる整数 p = \lfloor x \rfloor, \, 0\le q \le n-1 を取ると, np + q \le nx < np + q+1 であるから, \lfloor nx \rfloor = np + q となる。一方で,
\left\lfloor x + \frac{k}{n} \right\rfloor = \begin{cases} p & k \le n-1-q, \\ p+1 & k \ge n-q \end{cases}
であるから,
となり,結局 \lfloor nx \rfloor = \sum_{k=0}^{n-1} \lfloor x + k/n \rfloor である。
また,
p' - (q'+1)/n < x \le p' - q'/n となる整数 p' = \lceil x \rceil, \, 0\le q' \le n-1 を取ると, np' - q'-1< nx \le np' - q' であるから, \lceil nx \rceil = np' - q' となる。一方で,
\left\lceil x - \frac{k}{n} \right\rceil = \begin{cases} p'-1 & k \ge n-1-q', \\ p' & k \le n-q' \end{cases}
であるから,
となり, \lceil nx \rceil = \sum_{k=0}^{n-1} \lceil x - k/n \rceil . である。
証明終
床関数を用いた四捨五入した関数の表示
x> 0 に対し, x の小数点以下を四捨五入した関数 \color{red} \lceil x \rfloor は
\color{red} \lceil x \rfloor = \lfloor x + 1/2 \rfloor
と,床関数を用いて表せます。知っておくとよいでしょう。