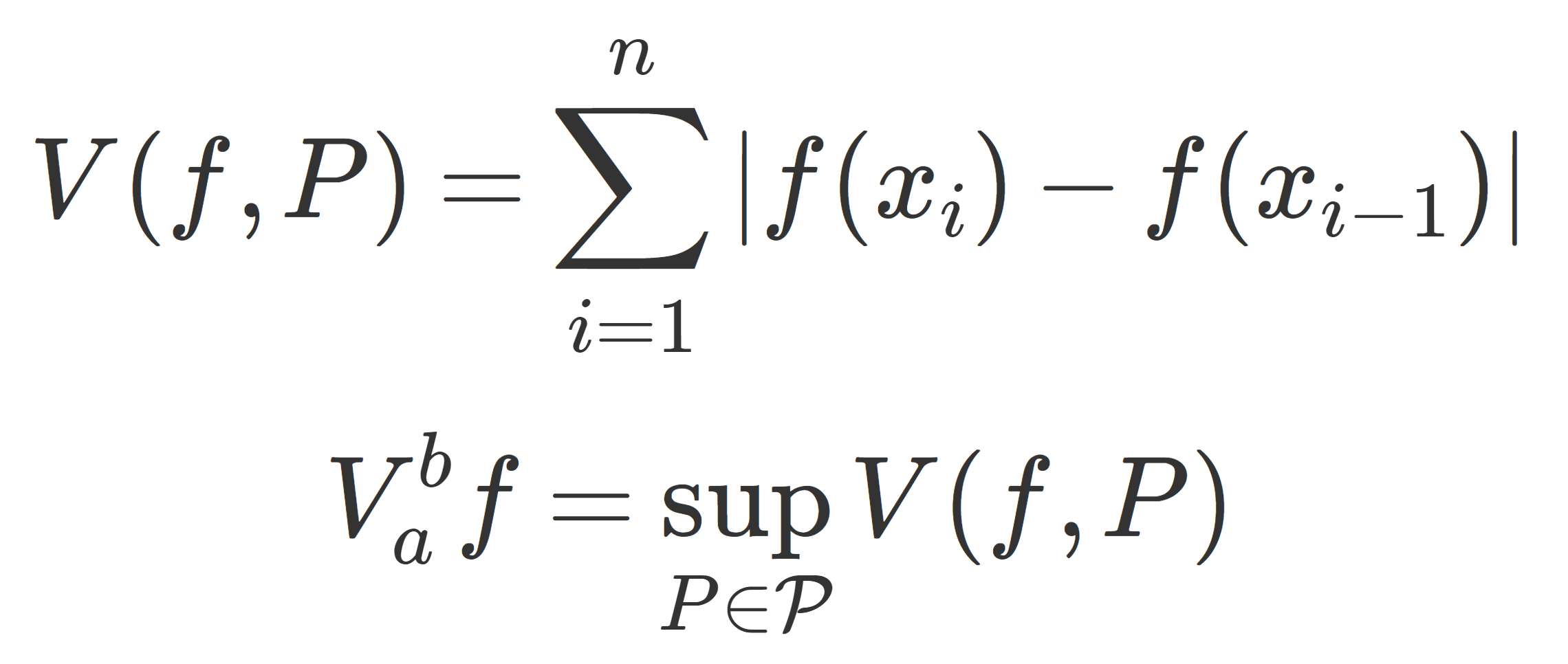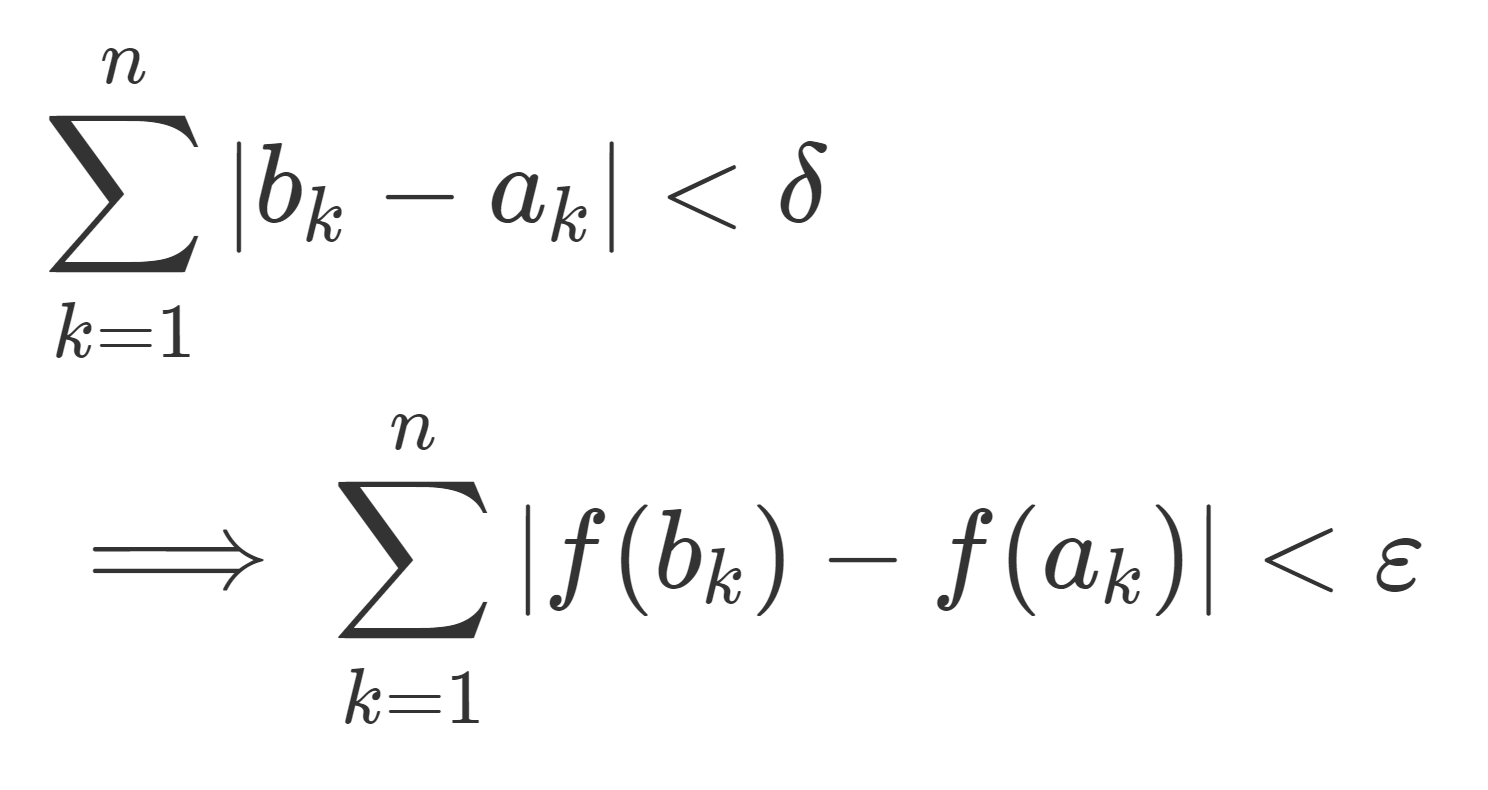有界変動関数とは,「変動」つまり上下にどのくらい動くかが,「有界」すなわちそんなに変動しないということです。有界変動関数は,2つの単調増加関数の差で表すことができることが知られています。
有界変動関数について,その定義と,大事な性質を証明付きで紹介していきましょう。
有界変動関数の定義
定義(全変動・有界変動関数)
f\colon [a,b]\to \R を関数とする。さらに,分割を
\small P=\{ \{x_i\}\mid n\ge 1,\, a=x_0<x_1<\dots <x_n=b\}
とする。分割 P における f の変動 (変分; variation) を
で定義する。分割 P 全体の集合を \mathcal{P} としたとき,
を f の全変動 (total variation) という。 \large \color{red} V_a^b f<\infty となるとき,f を有界変動関数 (function of bounded variation) という。
分割 P における変動は, \sum_{i=1}^{n} |f(x_{i})-f(x_{i-1})| の形をしていますから,以下のように,上下にどれだけ動いたかの和になります。
分割を変えて,その上限(sup)を取ると言っています。絶対値に関する三角不等式から,分割は細かければ細かいほど変動は大きくなります。よって全変動とは,関数自体がどれだけ上下するかを表しているといえます。有界変動関数とは,めちゃくちゃ上下するわけではないよ,ということです。
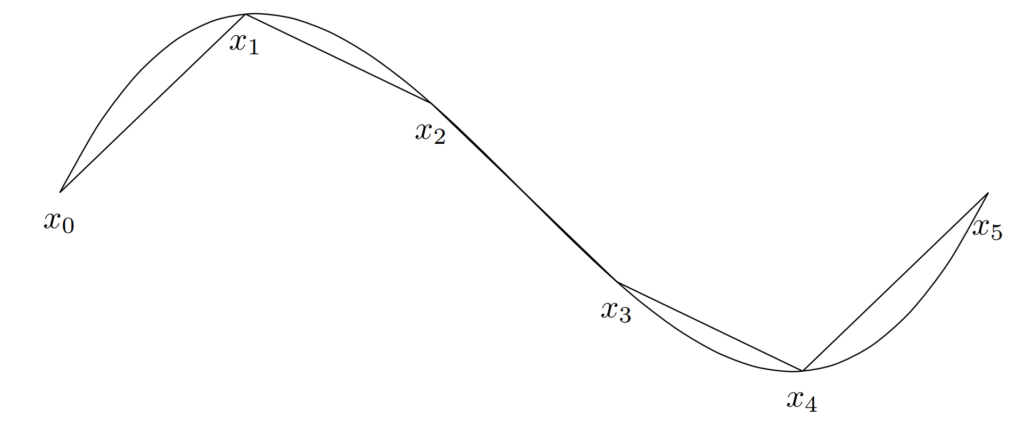
例を見た方が早いと思うので,見ていきましょう。
有界変動関数の例・そうでない例
有界変動関数の例
f \colon [a,b]\to\R が広義単調増加関数のとき,有界変動である。
同様に,区分的に単調関数(すなわちある a=x_0<x_1<\dots <x_n=b が存在して,各 [x_{i-1}, x_i] 上単調関数)のとき,有界変動である。
単調であれば連続でなくて構いません。たとえば,床関数 f(x)=\lfloor x\rfloor は a\le x\le b で広義単調増加なため,有界変動です。また, f が単調のとき, V_a^b f = |f(b)-f(a)| となります。実際, f が単調増加なら,
\begin{aligned}V_a^b f &=\sum_{i=1}^n |f(x_i)-f(x_{i-1})| \\ &= \sum_{i=1}^n (f(x_i)-f(x_{i-1})) \\ &=f(b)-f(a) \end{aligned}
となりますね。単調減少でも同様です。
有界変動関数でない例1
f\colon [0,1]\to \R を f(x)=\begin{cases} 1/x & 0<x\le 1, \\ 0 & x=0\end{cases} とすると,これは有界変動関数でない。
0<s<1 に対し, V_a^b f\ge |f(s)-f(0)|=1/s \xrightarrow{s\to\infty} \infty から分かります。この例は,関数が有界でない例です。
有界変動関数でない例2
f\colon [0,1]\to \R を f=1_{\mathbb{Q}} = \begin{cases} 1 & x\in \mathbb{Q}\cap [0,1] , \\ 0 & \text{otherwise} \end{cases} と定めると,これは有界関数だが,有界変動関数でない。
ディリクレ関数ですね。ディリクレ関数の定義と性質5つで詳しく解説しています。
関数としては有界ですが,無数に 0 に行ったり 1 に行ったりすることから,有界変動ではないです。
有界変動関数でない例3
f\colon [0,1]\to \R を
f(x)=\begin{cases} x\sin (1/x)& x\ne 0,\\ 0 & x=0\end{cases}
で定めると,これは連続関数であるが有界変動関数ではない。
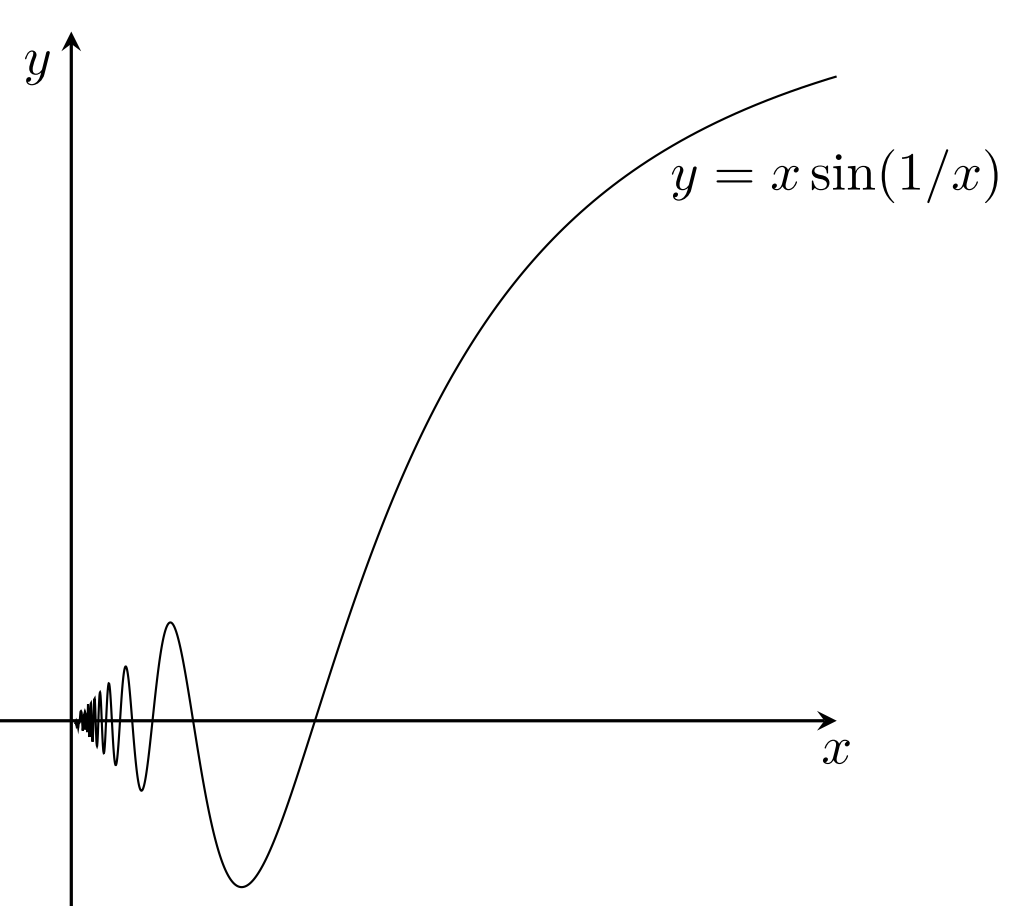
実際, 1\le k\le n に対し, t_k=\frac{2}{(2k+1)\pi} とすると,
\begin{aligned}& |f(t_{k+1})-f(t_k)| = t_{K+1}+t_k \\&\ge 2t_{k+1} \ge \frac{4}{3\pi(k+1)}\end{aligned}
であり,\sum_{k=1}^n \frac{4}{3\pi(k+1)}\xrightarrow{n\to\infty} \infty となるため,有界変動関数ではありません。めちゃくちゃ上下に振動しまくることからも,有界変動でないことは想像できるでしょう。
有界変動関数の大事な性質
1. 有界変動関数の基本的性質
定理1(有界変動関数の基本的性質)
f,g\colon [a,b]\to \R を有界変動関数とする。さらに c\in \R, \|f\|_\infty = \sup_{x\in [a,b]} |f(x)| とする。このとき,
- \color{red} \|f\|_\infty \le |f(a)|+V_a^b f 特に f は有界である。
- V_a^b f=0 \iff f は定数関数
- \color{red}V_a^b (f+g)\le V_a^b f +V_a^b g 特に, f,g が有界変動ならば, f+g も有界変動である。
- \color{red} V_a^b (cf) = |c|V_a^b f である。特に, f が有界変動ならば, cf も有界変動である。
- V_a^b(fg)\le \|f\|_\infty V_a^b g +\|g\|_\infty V_a^b f
- V_a^b|f|\le V_a^b f
- V_a^b f=V_a^c f+V_c^b f,\; a<c<b
- f が C^1 級であるとき, V_a^b f=\int_a^b|f'(t)|\, dt
証明
1. \|f\|_\infty \le |f(a)|+V_a^b f について 任意の a\le x\le b に対して,
\begin{aligned}|f(x)|&\le |f(a)|+|f(x)-f(a)| \\&\le |f(a)|+V_a^b f \end{aligned}
である。したがって, \|f\|_\infty \le |f(a)|+V_a^b f である。
2,3,4.はほぼ明らかなので省略する。
5. V_a^b(fg)\le \|f\|_\infty V_a^b g +\|g\|_\infty V_a^b f について
\begin{aligned}&|f(x_i)g(x_i)-f(x_{i-1})g(x_{i-1})| \\&\le |f(x_i)||g(x_i)-g(x_{i-1})| \\&\quad \qquad+|g(x_{i-1})||f(x_i)-f(x_{i-1})| \\ &\le \|f\|_\infty |g(x_i)-g(x_{i-1})| \\&\quad\qquad +\|g\|_\infty |f(x_i)-f(x_{i-1})| \end{aligned}
である。分割を細かくとると, V_a^b(fg)\le \|f\|_\infty V_a^b g +\|g\|_\infty V_a^b f である。
6,7.もほぼ明らかなため省略する。
8. V_a^b f=\int_a^b|f'(t)|\, dt について 各分割 P に対し,平均値の定理より,
V(f, P) = (x_i-x_{i-1}) |f'(t_{i})|,\quad x_{i-1} \le t_i\le x_i
とできる。 f' は連続であるため,リーマン積分の定義より,分割を細かくすると,右辺は \int_a^b |f'(t)|\, dt に収束する。よって示された。
証明終
2. 有界変動関数は単調増加関数の差にかける
定理2(ジョルダンの定理; Jordan’s theorem)
f\colon [a,b]\to\R が有界変動関数である必要十分条件は, f が広義単調増加関数の差にかけることである。
さらに, f を有界変動関数とするとき,広義単調増加関数 p, n\colon [a,b]\to\R であって,
- p(a)=n(a)=0
- f(x)-f(a)= p(x)-n(x),\quad x\in [a,b]
- V_a^x f =p(x)+n(x),\quad x\in [a,b]
をみたすものが一意的に存在する。
証明
広義単調増加関数自体は有界変動関数であるから,「広義単調増加関数の差でかける \implies 有界変動関数である」はよい。逆を示そう。
a\le x\le b に対し, v(x)=V_a^b f とする。さらに,
\begin{aligned} p(x)&= \frac{1}{2}\{ v(x)+f(x)-f(a)\} , \\ n(x)&= \frac{1}{2} \{ v(x)-f(x)+f(a)\} \end{aligned}
と定める。このとき,1,2,3.は明らかである。 a\le x<y\le b とすると,
より,p は広義単調増加である。同様の議論により,n も広義単調増加だとわかる。一意性は,2.3を同時にみたす p, n は明らかに一意なのでよい。
証明終
定理2より,以下の定理3が従います。
3. 有界変動関数はほとんどいたるところ連続・微分可能
定理3(有界変動関数はほとんどいたるところ連続・微分可能)
有界変動関数は高々可算個の点を除いて連続である。また,ほとんどいたるところ微分可能である。
これは,有界変動関数が単調関数の差にかけることと,単調関数は高々可算個の点を除いて連続で,ほとんどいたるところ微分可能であることから,直ちに従います。
4. 有界変動関数の空間はバナッハ空間
以下では,有界変動関数 f\colon [a,b]\to\R 全体の集合を \color{red}BV[a,b] と表すことにします。
定理4(有界変動関数の空間)
BV[a,b] は
\large \color{red} \|f\|_{BV} = |f(a)|+ V_a^b f
により,バナッハ空間になる。さらにいえば,バナッハ代数(バナッハ環)になる。
単に \|f\|= V_a^b f と定義すると,これはセミノルムにしかなりません。実際, V_a^b (f-g)=0 のとき,定理1の2.より f-g は定数といえますが,f=g とまでは言えません。
証明
定理1より, \|f\|_{BV} がノルムであることは良い。完備性を示そう。 \{ f_n\} を \|\cdot \|_{BV} におけるコーシー列とする。
定理1の1.より, \{f_n\} は一様収束位相に関してもコーシー列である。有界関数に一様収束位相を入れた空間 B[a,b] は完備なため, \{f_n\} はある関数 f \in B[a,b] に一様収束する。
\varepsilon >0 とする。このとき,ある N\ge 1 が存在して,m,n \ge N\implies \|f_m-f_n\|_{BV}\le \varepsilon とできる。 P を [a,b] の分割とする。このとき, n\ge N に対し,
\begin{aligned} &|f(a)-f_n(a)| +V(f-f_n, P) \\ &=\lim_{m\to\infty} \{ |f_m(a)-f_n(a)| +V(f_m-f_n, P)\} \\ &\le \sup_{m\ge N} \|f_m-f_n\|_{BV} \le \varepsilon \end{aligned}
となる。分割を細かくすることで, \|f-f_n\|_{BV}\le \varepsilon が従い,特に f\in BV[a,b] である。さらに, \lim_{n\to\infty} \|f-f_n\|_{BV} =0 となるため,完備性は示せた。
最後に,バナッハ代数であることを示す。 f_1,f_2\in BV[a,b] に対し, \|f_1f_2\|_{BV}\le \|f_1\|_{BV}\|f_2\|_{BV} を示せばよい。定理2を利用して,
\begin{aligned} f_1&=p_1-n_1+f_1(a), \\ f_2&= p_2-n_2+f_2(a) \end{aligned}
とする。このとき, \|f_1\|_{BV}= p_1(b)+n_1(b)+|f_1(a)| であり, \|f_2\|_{BV} も同様である。また,
であり,右辺を展開して,定理1の3.を用いて,かつ V_a^b(p_1p_2)=p_1(b)p_2(b) などを利用すれば,題意は示される(ただの面倒な計算なので省略)。
証明終
その他の重要な話
f が有界変動関数のとき, g を連続関数として,
\begin{aligned}\int g\, df=\sup_{P\in\mathcal{P}} \sum_{i=1}^n g(c_i)( f(x_i)-f(x_{i-1})),& \\ x_{i-1}\le c_i\le x_i & \end{aligned}
が定義でき,これをリーマン・スティルチェス積分 (Riemann–Stieltjes integral) といいます。リーマン・スティルチェス積分は,また別の記事で紹介しましょう。