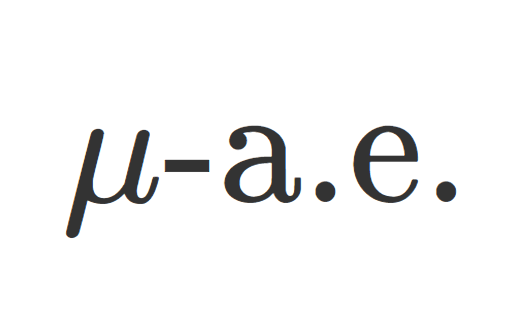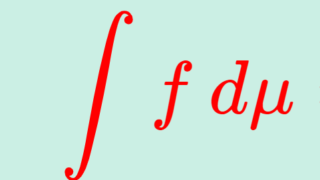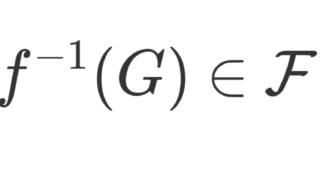測度論においては,ほとんどいたるところ(almost everywhere, a.e.)を用いた議論が頻繁に出てきます。 「ほとんどいたるところ」の定義と具体例について,丁寧に解説しましょう。
ほとんどいたるところ(almost everywhere, a.e.)の定義
定義(ほとんどいたるところ)
(X,\mathcal{F}, \mu) を測度空間とする。
可測関数に関する命題 P がほとんどいたるところ(almost everywhere, a.e., almost all, a.a.) で成立するとは,ある零集合 N\in\mathcal{F}(すなわち \mu(N)=0 となる N\in\mathcal{F})が存在して,X\setminus N 上の各点で成立することを言う。
このことを \color{red}P, \, \mu\text{-a.e.} や(測度 \mu が文脈上明らかなときは) \color{red}P,\, \text{a.e.} とかいたり, \color{red}P,\, \text{a.e. }x\in X とかくこともある。
「ほとんどいたるところ」というのは非常にあいまいな言葉で,数学用語とは思えないかもしれませんが,厳密な数学用語です。
定義だけ見ても意味わからないでしょうから,具体例を確認していきましょう。
ほとんどいたるところ(almost everywhere, a.e.)の具体例
例1.
\color{red} f(x)=0,\; \mu\text{-a.e.} とは,ある零集合 N\in\mathcal{F} が存在して, f(x) = 0 \;\, (x\in X\setminus N) となることをいう。すなわち,\mu(f\ne 0) = 0 である。
\{f\ne 0\} とは \{ x\in X\colon f(x)\ne 0\} の意味です。 f は可測なので, \{f\ne 0\}\in \mathcal{F} となります。
たとえば,ディリクレ関数 1_\mathbb{Q}(x)=\begin{cases} 1& x\in \mathbb{Q},\\ 0 & x\in\mathbb{R}\setminus\mathbb{Q}\end{cases} は関数 \mathbb{R}\to \mathbb{R} とみると \color{red}1_\mathbb{Q}=0 \; \text{a.e.} です。\mu をルベーグ測度としたとき, \mu(\mathbb{Q})=0 だから(→ボレル集合とは~定義と性質~)ですね。
例2.
\color{red} f=g,\; \mu\text{-a.e.} とは,ある零集合 N\in\mathcal{F} が存在して, f(x) = g(x) \;\, (x\in X\setminus N) となることをいう。すなわち,\mu(f\ne g) = 0 である。
\{f\ne g\} = \{ x\in X\colon f(x)\ne g(x)\} の意味です。
等号を不等号にしても同じです。
例3.
\color{red} f\le g,\; \mu\text{-a.e.} とは,ある零集合 N\in\mathcal{F} が存在して, f(x) \le g(x) \;\, (x\in X\setminus N) となることをいう。すなわち,\mu(f> g) = 0 である。
例4.
\color{red} f\ne g,\; \mu\text{-a.e.} とは,ある零集合 N\in\mathcal{F} が存在して, f(x) \ne g(x) \;\, (x\in X\setminus N) となることをいう。すなわち,\mu(f=g) = 0 である。
極限挙動にも使われます。
例5.
\color{red} f_n \to f,\; \mu\text{-a.e.} とは,ある零集合 N\in\mathcal{F} が存在して, N 以外の各点 x\in X\setminus N で f_n(x) \to f(x) となることをいう。すなわち,\mu(f_n \not\to f) = 0 である。
前提として, \{f_n\} は可測関数の列とします。 \{f_n\not\to f\} = \{ x\in X\colon f_n(x)\not\to f(x)\} の意味です。
ほとんどいたるところの基本的性質
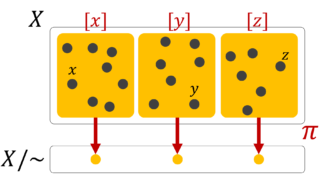
定理(a.e.は同値関係)
同値関係とは,同じものと思える関係のことです。関数解析においては,可測関数の集合をこの同値関係による同値類で割った集合を考えることが普通です。
定理(a.e.で等しい関数の積分は等しい)
(X,\mathcal{F},\mu) を測度空間とし, f,g\colon X\to\mathbb{R} を可測関数とする。 f が可積分かつ f=g,\; \mu\text{-a.e.} のとき, g も可積分で
\large \color{red} \int f\,d\mu = \int g\, d\mu.ほとんどいたるところ等しい関数は,積分は同じというわけです。測度論において「ほとんどいたるところ等しい」とは,積分を区別する必要がないことを意味しているわけです。特に, f=0,\; \text{a.e.} なら \int f\, d\mu =0 です。また, f\ge 0 ならば,この逆 \int f\, d\mu =0\implies f=0,\;\text{a.e.} も成立します。
これについては,以下の記事の後半の方で証明しています。