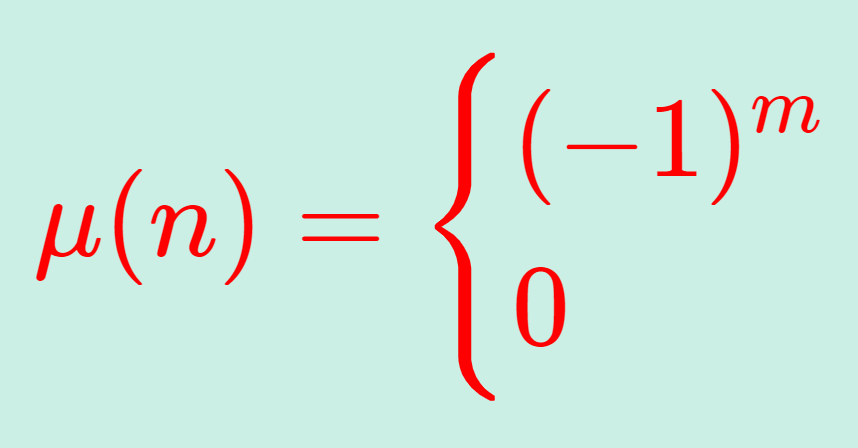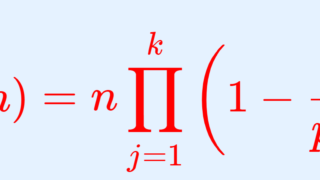メビウス関数とは,数論的関数の1つで,数論において重要な役割を果たします。メビウス関数の定義と,メビウスの反転公式の証明を行いましょう。
メビウス関数とは
定義(メビウス関数)
\mu\colon \mathbb{Z}_{\ge 1} \to \{ -1,0,1\} が \color{red}\mu(1) = 1 で, n\ge 2 のときは n=p_1^{a_1} p_2^{a_2}\dots p_m^{a_m} を素因数分解としたとき,
\color{red}\mu(n) = \begin{cases} (-1)^m & a_1=\dots = a_m=1,\\ 0 & \text{otherwise}\end{cases}
と定める。\mu をメビウス関数 (Möbius function) という。
同じ素数で2回割り切れる(平方因子をもつ)ときには 0 と定義し,そうでないときは素数の個数が奇数個なら -1,偶数個なら 1 と定義したものが「メビウス関数」ですね。
たとえば,\mu(2)=-1,\,\mu(3)=-1, \, \mu(4)=0,\, \mu(6)=1,\, \mu(10)=1,\, \mu(20)=0 です。
メビウス関数の性質とその証明
メビウス関数の基本性質~乗法的・約数和~
定理1(メビウス関数の基本性質)
- メビウス関数は乗法的である。すなわち,m,n>0 を互いに素とすると,\color{red}\mu(mn)=\mu(m)\mu(n).
- \displaystyle \color{red} \sum_{d\mid n} \mu(d) =\begin{cases} 1 & n=1, \\ 0 & n\ge 2.\end{cases}
ただし,\sum_{d\mid n} とは n の正の約数全体で和を取ることを指す。
証明
1. \mu(mn)=\mu(m)\mu(n) について
m,n のうち,一方が同じ素数で2回割り切れるとき,mn もそうであるから,\\mu(mn)=0,\, \mu(m)\mu(n)=0 となって等号が成立する。
m,n のうち,一方が 1 であるとき,\mu(1)=1 なので \mu(mn)=\mu(m)\mu(n) は明らか。
m,n\ge 2 かつどちらも平方因子を持たないとき,m=p_1\dots p_s,\; n=q_1\dots q_t を素因数分解とすると, \mu(m)=(-1)^s, \; \mu(n)=(-1)^t である。m,n は互いに素より, p_1, \dots, p_s, q_1,\dots, q_t は全て異なる素数で, mn=p_1\dots p_sq_1\dots q_t なので \mu(mn)=(-1)^{s+t}. したがって, \mu(mn)=\mu(m)\mu(n).
2. \displaystyle \sum_{d\mid n} \mu(d) =\begin{cases} 1 & n=1, \\ 0 & n\ge 2.\end{cases} について
n=1 のときは明らか。n\ge 2 のとき, n=p_1^{a_1}\dots p_s^{a_s} を素因数分解とすると, n の約数のうち, q_1\dots q_t ( q_1,\dots, q_t は素数)の形をしたものは _{s}\mathrm{C}_t 個ある( s 個の素数 p_1, \dots, p_s から t 個の素数を選ぶ選び方)。二項定理より,
\begin{aligned}\sum_{d\mid n} \mu(d) &= \sum_{t=0}^s {}_s\mathrm{C}_t (-1)^t = (1-1)^s = 0. \end{aligned}証明終
メビウスの反転公式
定理2(メビウスの反転公式)
f,g\colon \mathbb{Z}_{\ge 1} \to\mathbb{C} が
\color{red}g(n)=\sum_{d\mid n} f(d)
をみたすならば
である。ただし,\sum_{d\mid n} とは n の正の約数全体で和を取ることを指す。
g を f の和で表していたのを「反転」させて, f を g で表しているわけですね。
証明
\displaystyle \sum_{d\mid n} \mu\left(\frac{n}{d}\right)g(d) =\sum_{d\mid n} \mu(d)g\left(\frac{n}{d}\right) は明らかなので, \displaystyle f(n) = \sum_{d\mid n} \mu\left(\frac{n}{d}\right)g(d) のみ示す。 g の定義より,
\begin{aligned} \sum_{d\mid n} \mu\left(\frac{n}{d}\right)g(d) = \sum_{d\mid n} \mu\left(\frac{n}{d}\right) \sum_{e\mid d} f(e). \end{aligned}
ここで, d\mid n かつ e\mid d をみたす組 (e,d,n) は e\mid n かつ d'\mid (n/e) をみたす組 (e, ed', n) と対応している(下図)ので,

定理1.2より, \displaystyle \sum_{d'\mid (n/e)} \mu(d') =\begin{cases} 1 & e=n,\\ 0& e<n\end{cases} であるから,
\sum_{e\mid n} f(e) \sum_{d'\mid (n/e)} \mu(d') =f(n).
したがって,題意は示された。
証明終
メビウスの反転公式を用いた具体例を一つだけ挙げておきましょう。1,2,\dots, m のうち, m と互いに素なものの個数を \phi(m) とかくとき,これをオイラー関数 (Euler function) といい, \sum_{d\mid n} \phi(d)=n が知られています(→オイラー関数の定義・性質4つとその証明)。
これにメビウスの反転公式を適用することで,
\phi(n) =\sum_{d\mid n} \mu\left(\frac{n}{d}\right) d = \sum_{d\mid n} \mu(d)\frac{n}{d}
が分かりますね。