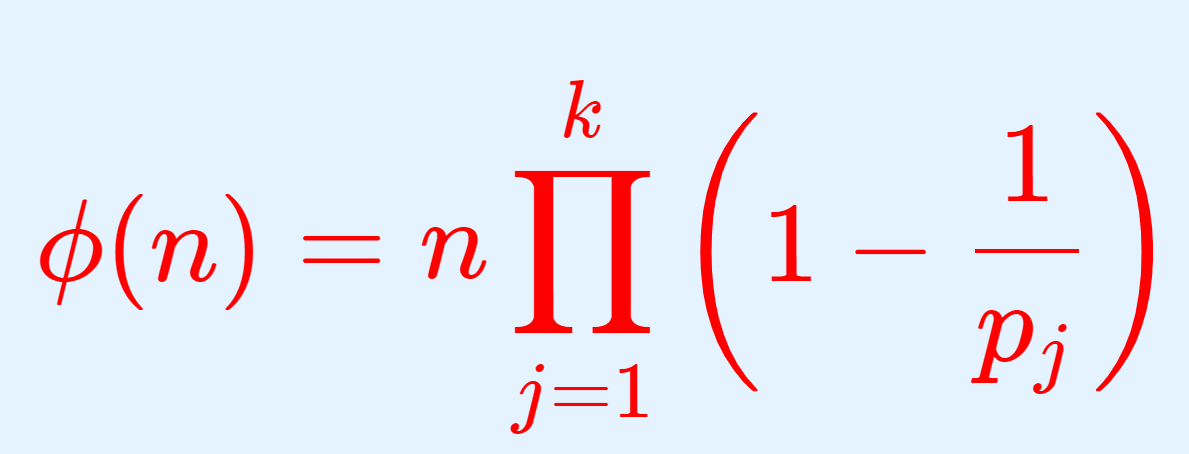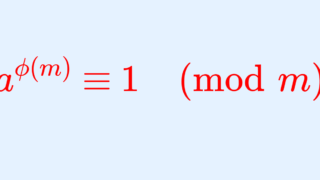オイラー関数,あるいはオイラーのファイ関数・オイラーのトーシェント関数とは, 1,2,3,\dots, n-1 のうち,n と互いに素なものの個数を指します。
これについて,その定義・性質を述べ,証明していきましょう。
オイラー関数(トーシェント関数)とは
定義(オイラー関数)
1,2,3,\dots, n-1 のうち,n と互いに素なものの個数を \color{red}\boldsymbol{\phi(n)} と表し,オイラー関数 (Euler’s function) またはオイラーのファイ関数,オイラーのトーシェント関数 (Euler’s totient function) という。
「互いに素」とは,最大公約数が 1 であるということです。
たとえば, 1 から 9 のうち, 10 と互いに素なものは 1,3, 7,9 ですから, \phi(10)=4 になります。
定義から明らかに \phi(n)\le n-1 が成立しますね。
オイラー関数の性質とその証明
さて,ここからはオイラー関数の重要な性質を述べ,それを証明しましょう。
オイラー関数の性質
定理(オイラー関数の性質)
- m,n を互いに素な正の整数とするとき, \color{red}\phi(mn)=\phi(m)\phi(n) である(乗法的関数という)。
- n=p_1^{a_1}p_2^{a_2}\dots p_k^{a_k} を素因数分解とすると, \color{red}\begin{aligned}\phi(n)&= n\prod_{j=1}^k \left(1-\frac{1}{p_j}\right) \\&=\small{n\!\left(1-\frac{1}{p_1}\right)\! \!\left(1-\frac{1}{p_2}\right)\dots \left(1-\frac{1}{p_k}\right) }.\end{aligned}
- \color{red}\displaystyle \sum_{d\mid n}\phi(d) =n. ただし, \displaystyle \sum_{d\mid n} とは,n の正の約数 d 全体で和を取ることを指す。
- a,n を互いに素な整数とするとき,\color{red} a^{\phi(n)}\equiv 1 \pmod n (オイラーの定理→【数論】オイラーの定理とその2通りの証明)。
2.はオイラー関数の計算に便利ですね。たとえば, 1260=2^2\times3^2\times5\times 7 ですから,
\begin{aligned} \phi(1260) &= 1260(1-\frac{1}{2})(1-\frac{1}{3})(1-\frac{1}{5})(1-\frac{1}{7})\\ &= 288\end{aligned}
と計算できるわけです。
また,4.はフェルマーの小定理の一般化です。
オイラー関数の性質の証明
さて,証明していきましょう。
証明
1. \phi(mn)=\phi(m)\phi(n)\; (\operatorname{gcd}(m,n)=1) について
中国剰余定理より, m と互いに素な整数 a と, n と互いに素な整数 b の組 (a,b) に対し,
c\equiv a\pmod m,\quad c\equiv b\pmod n
となる, mn と互いに素である整数 c が mn を法としてただ一つ存在し,この対応は1対1である。これは, \phi(mn)=\phi(m)\phi(n) を意味する。
2. \phi(n)= n\prod_{j=1}^k \left(1-\frac{1}{p_j}\right) について
まず,素数のべき乗のときに成立することを示す。 p を素数,k を正の整数とし, n=p^k とする。p と互いに素でないものは,p の倍数であるから, \phi(p^k)=p^k-p^{k-1}=p^k(1-1/p) が成り立つ。
これと,1.より,結論を得る。
3. \sum_{d\mid n}\phi(d) =n について
A_d=\{x_{1}, x_{2}, \dots ,x_{\phi(d)}\} を,1,2,3,\dots, d-1 のうち,d と互いに素な整数の集合とする。
さらに T_d = \{(d, x)\mid x\in A_d\} とし, T= \bigcup_{d\mid n} T_d とする( T=\bigoplus_{d\mid n} A_d とかくこともある)。このとき,特に \#A_d= \# T_d =\phi(d),\; \# T = \sum_{d\mid n} \phi(d) である。
f\colon \{1,2,3\dots, n\} \to T
を f(m) = (n/d', {m}/{d'})\in T_{n/d'} \subset T(ただし d'=\operatorname{gcd} (m,n) )と定めると,これは全単射である。実際, f^{-1} (d,x) = (n/d) x となる。
したがって,\# T = \#\{1,2,3,\dots, n\}=n となって,結論を得る。
4. オイラーの定理について
以下で証明している。
証明終
3.の証明が少々難しいかもしれません。たとえば,n=10 で考えることにすると,f(1)=(10,1), f(2)= (5,1), f(3)=(10, 3), f(4)= (5, 2),f(5)=(2,1), f(6)= (5,3),f(7)=(10,7),f(8)=(5,4), f(9)= (10,9), f(10)=(1,1) となります。