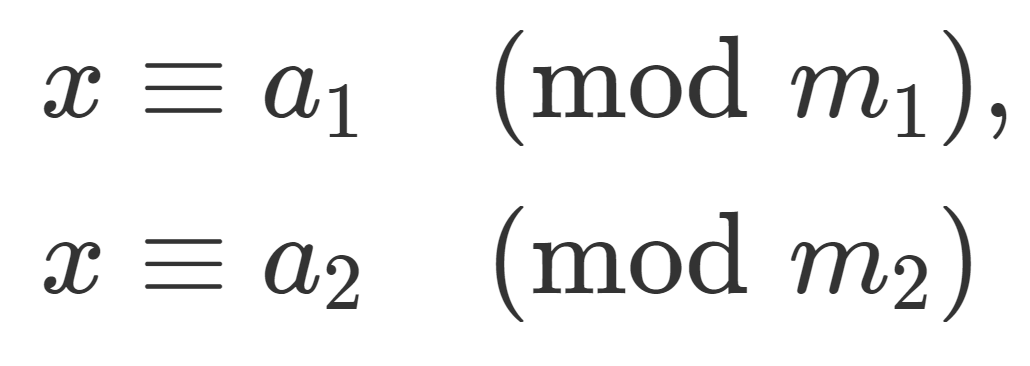中国剰余定理とは,複数の割り算の余りに関する定理です。中国式剰余定理とも言います。
中国剰余定理について,その主張と詳しい証明を解説していきます。
中国剰余定理
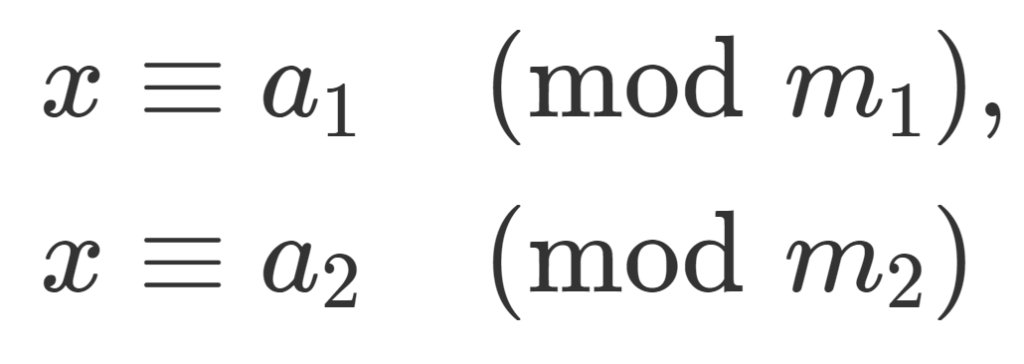
2元における中国剰余定理
まずは,2元における中国剰余定理を紹介します。
中国剰余定理1 (Chinese remainder theorem)
m_1, m_2>0 を互いに素な整数とする。このとき, a_1, a_2\in\mathbb{Z} に対し,
\color{red}\begin{aligned} x&\equiv a_1 \pmod {m_1}, \\ x&\equiv a_2 \pmod {m_2} \end{aligned}
をみたす x\in\mathbb{Z} が \bmod \,m_1m_2 において一意に存在する。
「 \bmod \,m_1m_2 において一意に存在」とは, x,y\in\mathbb{Z} をどちらも求める解とすると, x\equiv y \pmod{m_1m_2} となることを言います。
また,逆に x\in\mathbb{Z} を求める解とすると, x+m_1m_2 n \;(n\in\mathbb{Z}) も求める解になります。当てはめてみればわかる話でしょう。
一つだけ例題を考えてみましょう。
例題.
x\equiv 2 \pmod 3 ,\, x\equiv 4 \pmod 7 をみたす整数 x を求めよ。
x= 3s+2 = 7t+4 となる s,t\in\mathbb{Z} が存在しますから, 3s-7t=2 であり,一次不定方程式を解く問題に帰着しますね。
たとえば (s,t)=(3,1) はこれをみたしますから, 3(s-3)=7(t-1) であり, (s,t)= (3+7n, 1+3n)\; (n\in\mathbb{Z}) となりますね。すると \color{red}x= 11+21n \; (n\in\mathbb{Z}) となって, \mod 3\cdot 7 について解は一意的に存在することになります。
一般における中国剰余定理
中国剰余定理2 (Chinese remainder theorem)
m_1, m_2,\dots, m_n >0 をどの2つも互いに素な整数とする。このとき, a_1, a_2,\dots, a_n\in\mathbb{Z} に対し,
\color{red}\begin{aligned} x&\equiv a_1 \pmod {m_1}, \\ x&\equiv a_2 \pmod {m_2},\\ &\;\; \vdots \\ x&\equiv a_n \pmod{m_n} \end{aligned}
をみたす x\in\mathbb{Z} が \bmod \,m_1m_2\dots m_n において一意に存在する。
2つのものを, n 個に拡張したわけですね。「どの2つも互いに素」とは, i\ne j に対して, \operatorname{gcd} (a_i,a_j)=1 となることを言います。
中国剰余定理の証明
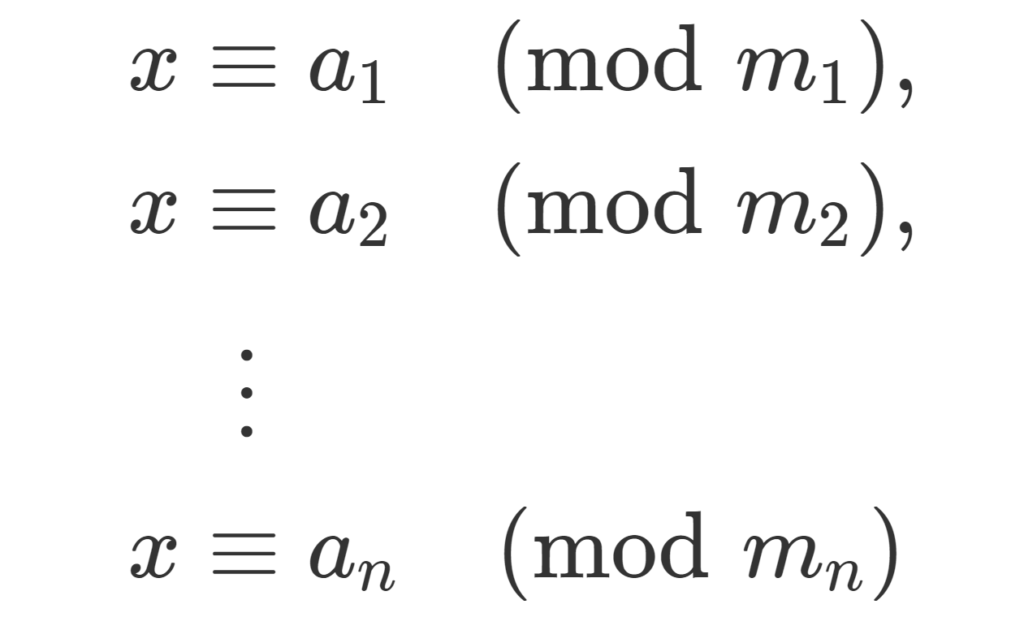
さて,ここからは証明にうつりましょう。定理を再掲して,それから証明します。
2元の場合の証明
m_1, m_2>0 を互いの素な整数とする。このとき, a_1, a_2 \in\mathbb{Z} に対し,
\begin{aligned} x&\equiv a_1 \pmod {m_1}, \\ x&\equiv a_2 \pmod {m_2} \end{aligned}
をみたす x\in\mathbb{Z} が \mod m_1m_2 において一意に存在する。
存在性と一意性に分けて証明しましょう。
証明
存在性について
m_1, m_2 は互いに素より, m_1s_1+m_2s_2=1 をみたす s_1, s_2\in\mathbb{Z} が存在する。
ここで, \color{red} \boldsymbol{x = a_2m_1s_1+a_1m_2s_2} とする。すると,
\begin{aligned}x&= a_2m_1s_1+a_1m_2s_2 \\ &= a_2m_1s_1 +a_1(1-m_1s_1)\\ &\equiv a_1 \pmod{m_1} \end{aligned}
であり,
なので,題意は示された。
一意性について
x, y を共に条件をみたすとする。このとき,
\begin{aligned}x-y&\equiv a_1-a_1 \equiv 0 \pmod{m_1} \\ x-y &\equiv a_2-a_2\equiv 0\pmod{m_2} \end{aligned}
なので, x-y は \operatorname{lcm}(m_1, m_2)=m_1m_2 の倍数である。これは, x\equiv y \pmod{m_1m_2} を意味する。
証明終
一般の場合の証明
m_1, m_2 ,\dots , m_n>0 をどの2つも互いに素な整数とする。このとき, a_1, a_2 ,\dots, a_n\in\mathbb{Z} に対し,
\begin{aligned}x&\equiv a_1 \pmod{m_1} ,\\ x&\equiv a_2 \pmod{m_2},\\ &\;\; \vdots \\ x&\equiv a_n \pmod{m_n} \end{aligned}
をみたす x\in\mathbb{Z} が\mod m_1m_2\dots m_n において一意に存在する。
一般の場合は,2元の場合から帰納的に証明できますが,ここでは独立に証明することにしましょう。
証明
存在性について
M=m_1m_2\dots m_n とおく。 i = 1,2,\dots, n に対し, M/m_i, m_i は互いに素であるから, \dfrac{M}{m_i}s_i+m_is'_i=1 となる s_i,s'_i\in\mathbb{Z} が存在する。
\displaystyle\boldsymbol{\color{red} x= \sum_{i=1}^n a_i \frac{M}{m_i} s_i} とする。j\ne i なら M/m_j\equiv 0\pmod{m_i} なので,
x\equiv a_i \frac{M}{m_i} s_i = a_i(1-m_is'_i)\equiv a_i \pmod{m_i}
より,存在性は示せた。
一意性について
x, y を共に条件をみたすとする。このとき, i=1,2,\dots, n に対して,
\begin{aligned}x-y&\equiv a_i-a_i \equiv 0 \pmod{m_i} \end{aligned}
なので, x-y は \operatorname{lcm}(m_1, m_2,\dots, m_n)=m_1m_2\dots m_n の倍数である。これは, x\equiv y \pmod{m_1m_2\dots m_n} を意味する。
証明終
環論における中国剰余定理
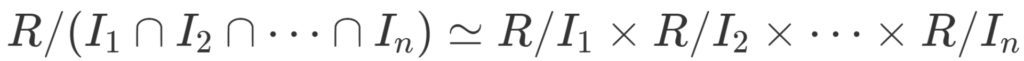
初等整数論における中国剰余定理をより一般に拡張したものが,環論における中国剰余定理です。これも紹介しましょう。
なお,ここからは環やイデアルの定義などの専門的な知識が必要です。簡単のため,(単位元を持つ)可換環としましょう。
環論における中国剰余定理とその系
中国剰余定理3 (Chinese remainder theorem)
R を可換環, I_1, I_2, \dots, I_n\subsetneq R をどの2つも互いに素(後述)なイデアルとする。このとき,
- i=1,2,\dots, n に対し, I_i と I_1 \cdots I_{i-1}I_{i+1}\cdots I_n は互いに素である。
- \color{red} I_1 \cap I_2 \cap \dots \cap I_n = I_1I_2\cdots I_n.
- \color{red} R/(I_1\cap I_2\cap \dots \cap I_n) \simeq R/I_1 \times R/I_2 \times \dots \times R/I_n.
ここでイデアル I,J が互いに素とは, I+J=R を意味します。
一般にイデアル I,J に対して, I+J も R のイデアルですから,互いに素であることの証明には,1\in I+J を示せばよいです。また, IJ = \{ xy\mid x\in I, \,x\in J\} も, R のイデアルになります。
この定理は,初等整数論における中国剰余定理2の一般化になっています。実際,可換環 \mathbb{Z} において,整数 m_i, m_j が互いに素であることは,イデアル m_i\mathbb{Z}, m_j\mathbb{Z} が互いに素であることに対応していて, \bmod\, m_i で考えることは, \mathbb{Z}/m_i\mathbb{Z} で考えることに対応しているからです。
具体的には以下の定理が,初等整数論における中国剰余定理に完全に対応しています。
中国剰余定理の系
m_1, \dots, m_n >0 はどの2つも互いに素な整数とする。このとき,
\color{red}\mathbb{Z}/m_1\cdots m_n\mathbb{Z} \simeq \mathbb{Z}/m_1\mathbb{Z}\times \dots\times \mathbb{Z}/m_n\mathbb{Z}.環論における中国剰余定理の証明
環論における中国剰余定理を証明しておきましょう。
証明
1.について
i=1 としても一般性を失わない。 j =2,\dots, n に対し, I_1, I_j は互いに素なので, x_j+y_j = 1 となる x_j\in I_1, \, y_j\in I_j が存在する。すると,
(x_2+y_2)\cdots (x_n+y_n) = 1\cdots 1=1
である。左辺を展開すると, y_2\cdots y_n \in I_2\cdots I_n であり,残りの項は x_i を少なくとも1つ含むので I_1 の元である。したがって, 1\in I_1 + I_2 \cdots I_n なので, I_1+ I_2 \cdots I_n =R である。
2.について
まず n=2 のときを考える。イデアルの定義より, I_1I_2\subset I_1\cap I_2 は明らか。
I_1+I_2=R より, x_1\in I_1,\, x_2\in I_2 で x_1+x_2=1 となるものが存在する。 a\in I_1\cap I_2 とする。このとき, ax_1+ax_2=a である。 ax_1, ax_2\in I_1I_2 なので, a\in I_1I_2 である。
ゆえに I_1\cap I_2 \subset I_1I_2 なので, I_1\cap I_2 = I_1I_2 である。
一般の n については,1.と帰納法を用いて,
I_1I_2 \cdots I_n = I_1 \cap (I_2 \cdots I_n) = \bigcap_{i=1}^n I_i.3.について
まず n=2 のときを考える。準同型
f\colon R \ni a \mapsto (a+I_1, a+I_2) \in R/I_1\times R/I_2
について, \operatorname{Ker }f = I_1 \cap I_2 である。2.で定めた x_1,x_2 を用いる。任意の a,b\in R に対し,
であるから, f は全射である。したがって準同型定理より,
を得る。一般の n については1,2.と帰納法により,
が分かる。
証明終