ルジャンドルの定理,あるいはルジャンドルの公式とは, n! が素数 p で何回割れるかを表したものです。これについて,定理の主張と証明を行いましょう。
ルジャンドルの定理
ルジャンドルの定理 (Legendre’s formula)
n を正の整数,p を素数とする。このとき, n!=1\cdot 2\cdot 3 \cdots n は p で
\color{red} \sum_{k=1}^\infty \left\lfloor \frac{n}{p^k}\right\rfloor = \left\lfloor \frac{n}{p}\right\rfloor+\left\lfloor \frac{n}{p^2}\right\rfloor+\left\lfloor \frac{n}{p^3}\right\rfloor+\cdots
回割り切れる。ただし, \lfloor \cdot \rfloor は床関数(ガウス記号)である。
無限和の形をしていますが,実質有限和です。なぜなら,n< p^k のときは \lfloor n/p^k\rfloor =0 ですから, n<p^k となる最小の k を k_0 とすると,
\sum_{k=1}^\infty \left\lfloor \frac{n}{p^k}\right\rfloor =\sum_{k=1}^{k_0-1} \left\lfloor \frac{n}{p^k}\right\rfloor
となるからです。
ルジャンドルの定理の証明
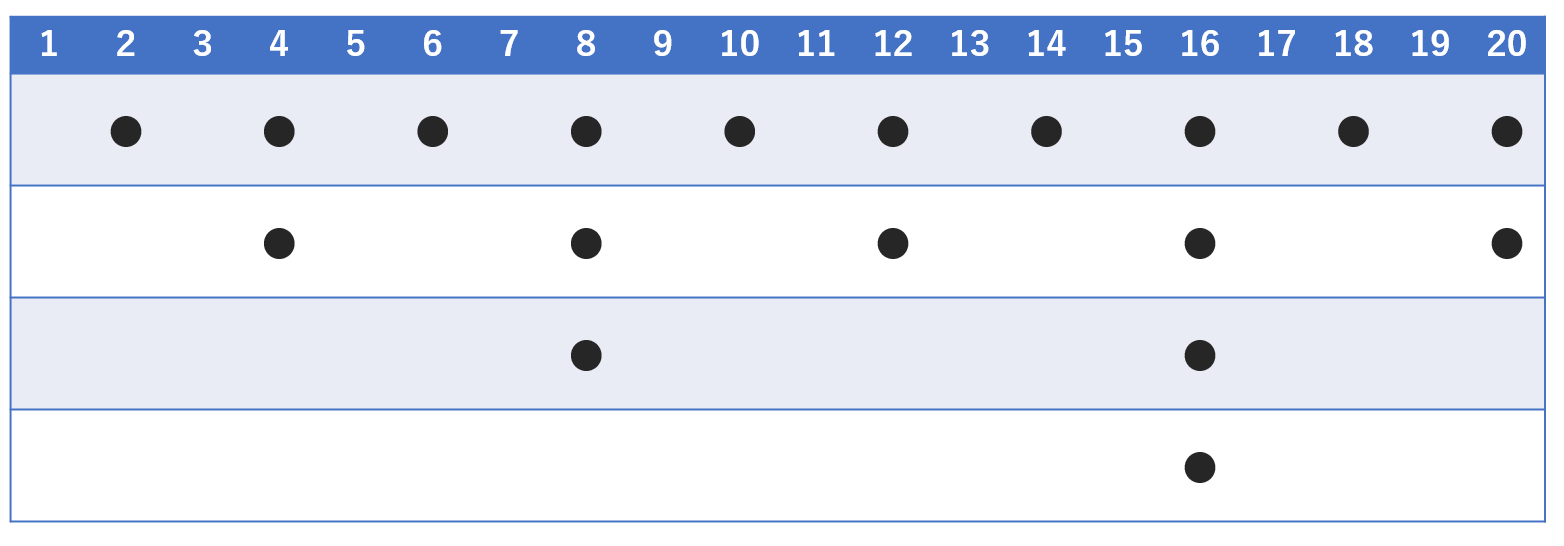
たとえば, 1 から 20 までの積が, 2 で何回割れるか考えることにしましょう。
整数 m が 2 で s 回割れて, n が t 回割れるとき,積 mn は 2 で s+t 回割れますね。これを応用すれば,
1,2,3,\dots, 20 それぞれの数が, 2 で何回割れるかを数えて,それを足し上げればよいということが分かります。ここで, 1 から 20 までのそれぞれの数が, 2 で何回割れるかを●で表したのが以下の図です。●の個数が2で何回割れるかに対応しています。
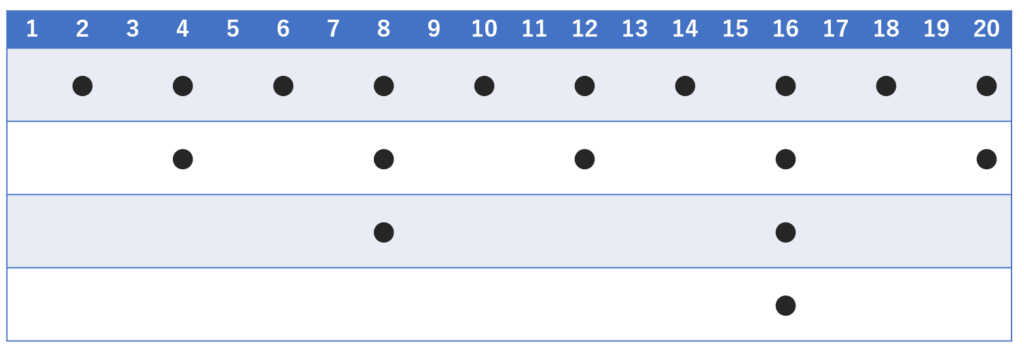
この図を縦ではなく横に見ることにしましょう。 2 で割れるものは2つごとに現れ, 4 で割れるものは4つごとに現れますから,横で見ると1段目の●の数は 20\div 2 の商の数だけあり,2段目は 20\div 2^2 の商の数だけあります。以下のような感じですね。
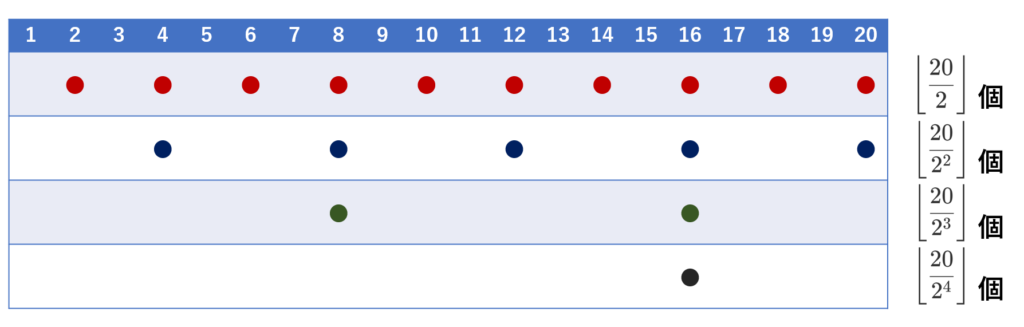
したがって,2で割り切れる回数は
\begin{aligned}&\left\lfloor \frac{20}{2}\right\rfloor +\left\lfloor \frac{20}{2^2}\right\rfloor+\left\lfloor \frac{20}{2^3}\right\rfloor +\left\lfloor \frac{20}{2^4}\right\rfloor\\ &=10+5+2+1=18 \end{aligned}
となるわけです。
一般の場合の証明は,これを応用すれば全く同じなので省略することにしましょう。
ルジャンドルの定理の適用例
一つだけ具体例を紹介しておきましょう。
例題
100! は 3 で何回割り切れるか。
ルジャンドルの定理を使えば,割り切れる回数は
\small \begin{aligned}&\sum_{k=1}^{\infty} \left\lfloor \frac{100}{3^k}\right\rfloor \\ &=\left\lfloor \frac{100}{3}\right\rfloor+\left\lfloor \frac{100}{3^2}\right\rfloor+\left\lfloor \frac{100}{3^3}\right\rfloor+\left\lfloor \frac{100}{3^4}\right\rfloor+\left\lfloor \frac{100}{3^5}\right\rfloor+\cdots \\ &= 33+ 11+3+1+0+\cdots\\ &= 48 \end{aligned}
より, 48 回と分かりますね。