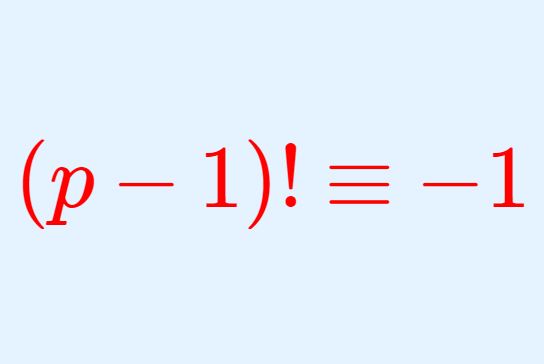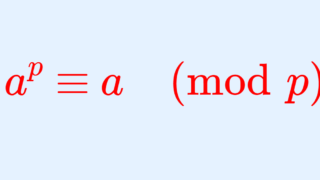数論(整数論)におけるウィルソンの定理とは (p-1)! \equiv -1 \pmod p のことを言います。これについて,定理の内容と証明4通りをわかりやすく紹介しましょう。
【(p-1)!≡-1】ウィルソンの定理
ウィルソンの定理 (Wilson’s theorem)
p を素数とするとき,
\large \color{red} (p-1)! \equiv -1 \pmod p
が成立する。逆に,上の式が成立するならば p は素数である。
「逆に~」の部分は素数判定に使えますが,実際これを素数判定に使おうと思うと,膨大な数の掛け算を考える必要があるため,あまり現実的ではありません。
定理の主張自体は高校生にも理解できるでしょう。証明についても,4通りのうち最初の2つは高校生でも理解可能だと思います。解説していきましょう。
ウィルソンの定理の証明4通り
「逆に~」以降の証明は簡単です。p が素数でないとすると, p=p_1^{a_1}p_2^{a_2} \dots p_n^{a_n} のように素因数分解できて,
n\ge 2 のときは, 1,2,\dots, p-1 の中に数 p_1^{a_1}, p_2^{a_2},\dots, p_n^{a_n} がありますから,それらをかけ算すると (p-1)! \equiv 0 \pmod p ですね。
n=1 であっても, (p-1)! は p_1 の倍数になるため, (p-1)!-1 が p_1 の倍数になることはなく, (p-1)! \not\equiv -1 \pmod p です。
よって,示すべきは定理の前半部分: p は素数ならば (p-1)! \equiv -1 \pmod p です。これについて,4通りの方法で証明しましょう。
互いに積が1になる組に分ける基礎的な証明
証明
p=2 では明らかなので p\ge 3 とする。 1,2,\dots, p-1 は p と互いに素なので,各 1\le x\le p-1 について xx^* \equiv 1 \pmod p となる 1\le x^*\le p-1 がただ一つ存在する。ここで,
\begin{aligned}x=x^* &\iff x^2 \equiv 1 \\&\iff (x+1)(x-1)\equiv 0 \\&\iff x\equiv \pm 1 \\ &\iff x = 1, p-1\end{aligned}
であるから, 2, 3, \dots, p-2 は, xx^*\equiv 1 \pmod p となる2つずつの組( (p-3)/2 組)に分けられる。従って {}\bmod p で,
証明終
フェルマーの小定理を用いた基礎的な証明
続いては,フェルマーの小定理を用いた方法です。「フェルマーの小定理」については,フェルマーの小定理とその3通りの証明で解説しています。
証明
p=2 のときは明らかなので, p\ge 3 とする。
フェルマーの小定理より,整数 1\le x \le p-1 に対して, x^{p-1}\equiv 1 \pmod p である。 従って, f(x) = x^{p-1} -1 とすると, f(x) \equiv 0 \; (1\le x\le p-1) である。
f(x) を x-1 で割った商を f_1(x),余りを R_1 とすると, f(1) \equiv 0 なので, R_1 \equiv 0 である。したがって, f(x) \equiv (x-1)f_1(x) である。
同様に f_1(x) を x-2 で割った商を f_2(x),余りを R_2 とすることで, f_1(x)\equiv (x-2)f_2(x) がわかる。
f(x) は p-1 次式で最高次係数 1 であることも考慮すると,帰納的に {}\bmod p で
f(x) \equiv (x-1)(x-2)\dots (x-(p-1))
となる(剰余の定理)。両辺 x=0 を代入することで,
p は 3 以上と仮定したから奇数なので, -1\equiv (p-1)! \pmod p である。
証明終
Z/pZの乗法群が巡回群になることを用いた専門的な証明
さて,ここからは少しばかり専門的な証明も紹介します。証明の理解には,多少の代数学の専門的な知識が必要です。
証明
p=2 では明らかなので, p は奇素数とする。
有限体 \mathbb{Z}/p\mathbb{Z} の乗法群 (\mathbb{Z}/p\mathbb{Z})^\times は巡回群であるから,その生成元 a\in (\mathbb{Z}/p\mathbb{Z})^\times が存在する(原始根という)。 | (\mathbb{Z}/p\mathbb{Z})^\times | = p-1 に注意して, a,a^2,\dots, a^{p-1} は全て異なる元であるから, {}\bmod p で
a\cdot a^2 \cdots a^{p-1} \equiv 1\cdot 2 \cdots p-1 .
すなわち \color{red}a^{p(p-1)/2}\equiv (p-1)! である。フェルマーの小定理より,
なので, (a^{p(p-1)/2} -1) ( a^{p(p-1)/2} +1)\equiv 0\pmod p より, a^{p(p-1)/2} は 1 か -1 に合同である。a は位数 p-1 の巡回群の生成元であったから, a^m \equiv 1 となる m は p-1 の倍数であるが, p(p-1)/2 はそうではない。ゆえに a^{p(p-1)/2} \equiv -1\pmod p であり,赤字の式から結論を得る。
証明終
群論におけるシローの定理を用いた専門的な証明
さて,別の専門的な証明方法を紹介します。ここでも,群論の知識が必要です。
証明
対称群 S_p の位数 p の部分群の個数を考える。 |S_p| = p! であるから,位数 p の部分群はシロー p 部分群である。
ここで, p 次巡回置換の個数は, 1\mapsto x_1\mapsto x_2 \mapsto \dots \mapsto x_{p-1} \mapsto 1 となる相異なる整数 2\le x_1, x_2 ,\dots, x_{p-1} \le p の個数であるから, (p-1)! 個である。
シロー p 部分群の単位元以外の p-1 個の元は p 次巡回置換であるから,シロー p 部分群の個数は (p-1)!/(p-1)=(p-2)! 個である(異なるシロー p 部分群は単位元以外の元を共有しないことに注意)。
シローの定理より,シロー p 部分群の個数について, (p-2)!\equiv 1 \pmod p が成り立つ。従って,
(p-1)!\equiv 1\cdot (p-1) \equiv -1 \pmod p
である。
証明終
一番最初の証明に比べて,高級な道具を振り回している感がありますが,一応証明できましたね。