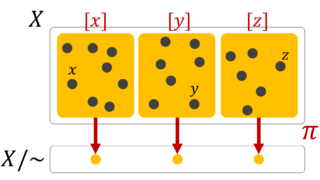
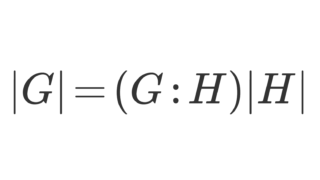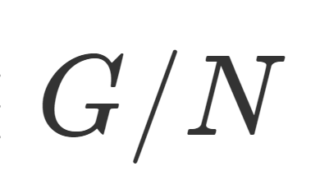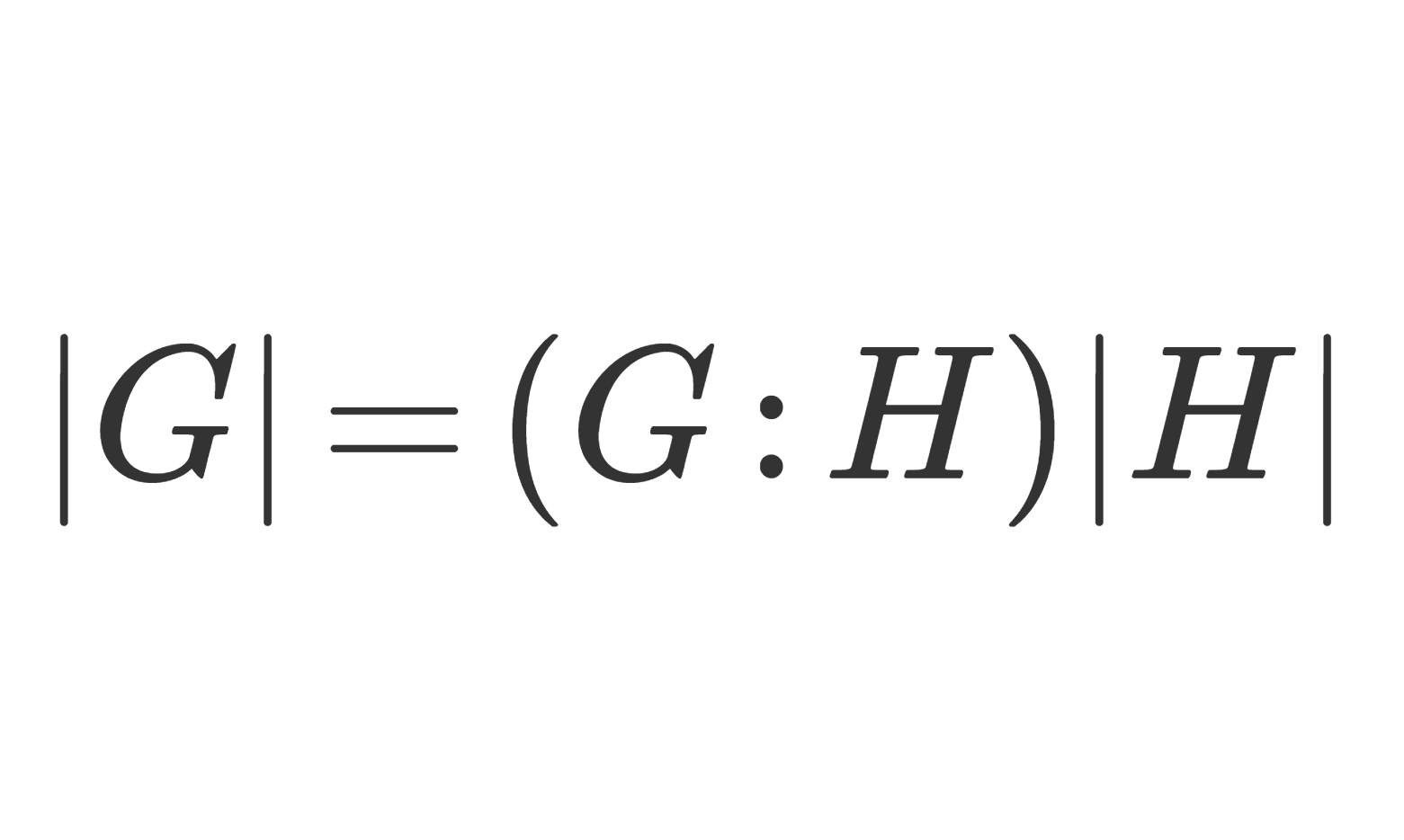群論における「剰余類(左剰余類・右剰余類)」と「剰余集合(左剰余集合・右剰余集合)」と「部分群の指数」の概念を，手順を追って解説していきます。
少々長いですが，群論における基本的で重要な概念ですから，ゆっくりと理解していきましょう。
剰余類～左剰余類・右剰余類～
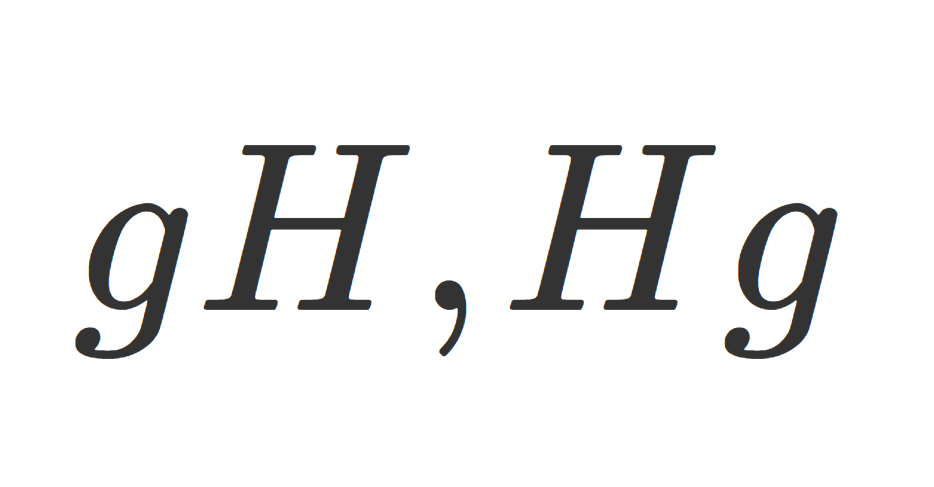
剰余類(左剰余類・右剰余類)の定義
定義1（左剰余類と右剰余類）
G を群， H\subset G をその部分群とする。このとき， g\in G に対し
\color{red}\large gH = \{ gh \mid h\in H\}\subset G
を G における H の左剰余類 (left coset) といい，
を G における H の右剰余類 (right coset) という。 G が可換群(アーベル群)のときは左右の違いがないため，単に剰余類 (coset) という。可換群(アーベル群)のときは演算を + でかく慣習から，剰余類は \color{red}g+H のようにかく。
注意ですが， g\ne g' \implies gH\ne g'H とは限りません。たとえば， H=G とすると，任意の g,g'\in G に対して， gG=g'G=G になります。ここでいう「＝」は集合としてのイコールです。
実際， gG\subset G であることは，任意の g'\in G に対して gg'\in G であることが分かります。逆に G\subset gG であることは，任意の g'\in G に対して，ある g''\in G が存在して， g^{-1}g' = g'' とでき，両辺左から g をかけることで g' = gg'' \in gG であることから分かります。
具体例を挙げましょう。
剰余類(左剰余類・右剰余類)の具体例
剰余類の例1.
3\mathbb{Z}\subset \mathbb{Z} を和(加法)に関する部分群と見る。このとき， \color{red} 3\mathbb{Z}, \,1+3\mathbb{Z},\, 2+3\mathbb{Z} は剰余類である。
また，集合として \cdots = -2+3\mathbb{Z}= 1+3\mathbb{Z} = 4+3\mathbb{Z}=\cdots となっている。
剰余類の例2.
S_3 を 3 次対称群とし， H=\{ e, (12)\} をその部分群とする。このとき，
\color{red}\begin{aligned}(13)H &= \{ (13), (123)\},\\ H(13) &=\{ (13), (132)\}\end{aligned}
はそれぞれ左剰余類・右剰余類である。また， A_3=\{ e, (123), (132)\} を 3 次交代群とすると，
はそれぞれ左剰余類・右剰余類である。特に (12)A_3=A_3(12) である。
置換の積は写像の合成と同様に，右から計算するものとします。 (i_1i_2i_3) とは， i_1\mapsto i_2\mapsto i_3\mapsto i_1 となる巡回置換を表します。
剰余類(左剰余類・右剰余類)は同値類
剰余類は，同値関係による同値類です。定理を述べましょう。
この節の理解には，同値関係・同値類の知識が必要です。以下が分からない場合，この節はいったん飛ばしても構いません。（が，「剰余群」などのさらに進んだ概念の理解にはすぐ必要になります）
定理1（剰余類は同値類）
G を群， H\subset G をその部分群とする。このとき， x,y\in G に対し， \color{red}xH =yH または \color{red} xH \cap yH=\emptyset のいずれかが成立する。 Hx,Hy についても同様である。また，
\color{red} \begin{gather}xH=yH\iff x^{-1} y \in H,\\ Hx=Hy \iff xy^{-1}\in H \end{gather}
が成立する。特に， x\sim y \stackrel{\mathrm{def}}{\iff} x^{-1} y\in H と定義すると， \sim は同値関係で， xH = \{ y\in G\mid x\sim y\} は同値類になっている。 Hx も同様である。
証明
xH=yH または xH\cap yH = \emptyset について
z\in xH\cap yH \ne \emptyset とすると， z=xh_1=yh_2 となる h_1, h_2\in H が存在する。特に， x = yh_2h_1^{-1}\in yH, \; y=xh_1h_2^{-1}\in xH. よって xH \subset yH, \; yH \subset xH であるから， xH=yH である。
xH=yH \implies x^{-1}y\in H について
xH=yH とすると，ある h_1, h_2\in H が存在して xh_1=yh_2 である。両辺左から x^{-1}，右から h_2^{-1} をかけて h_1 h_2^{-1}= x^{-1} y. よって x^{-1}y\in H.
x^{-1}y\in H \implies xH=yH について
x^{-1}y \in H の両辺左から x かけて y \in xH である。よって yH\subset xH なので， xH=yH である。
Hx=Hy \iff xy^{-1}\in H についても同様である。
「特に～」以下は xH=xH と xH=yH\implies yH=xH と xH=yH,yH=zH \implies xH=zH (集合としてのイコール)が成立することから， x\sim y は同値関係であり，y\in xH \iff x^{-1} y \in H から xH=\{ y\in G\mid x\sim y\} もわかる。
証明終
剰余類(左剰余類・右剰余類)の濃度は全て等しい
本記事では用いませんが，以下の定理は基本的です。
定理2（剰余類の濃度は全て等しい）
G を群， H\subset G をその部分群とする。このとき，任意の g\in G に対し，剰余類 gH, Hg と H の濃度(要素の個数)は等しい。すなわち，
\large \color{red}|gH| = |Hg| = |H|.証明
f\colon H\ni h \mapsto gh \in gH が全単射であることを示す。全射であることは明らか。また， gh_1 = gh_2 とすると，両辺左から g^{-1} かけて h_1=h_2 なので単射でもある。よって |H| = |gH| であり，あとは同様。
証明終
剰余類による商集合
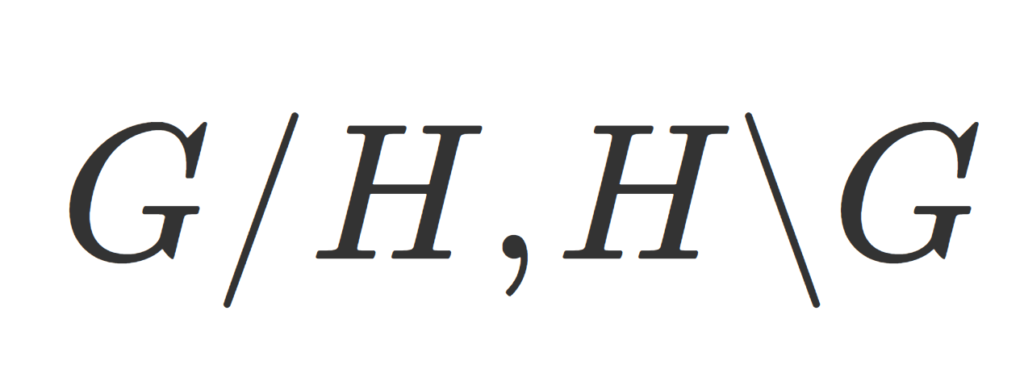
剰余集合(左剰余集合・右剰余集合)の定義
定義2（剰余類による商集合）
G を群， H\subset G をその部分群とする。このとき，左剰余類全体の集合
\color{red}\large G/H = \{ gH\mid g\in G\} \subset 2^G
を左剰余集合 (left factor set) という。左剰余集合は同値関係 x\sim y\iff x^{-1} y\in H による商集合になっている。
同様に，右剰余類全体の集合
\color{red}\large H\backslash G = \{ Hg\mid g\in G\} \subset 2^G
を右剰余集合 (right factor set) という。右剰余集合は同値関係 x\sim y\iff x y^{-1} \in H による商集合になっている。
G が可換群(アーベル群)のときは両者は一致するので，単に剰余集合 (factor set) という。
同値関係による商集合になっていることは，上の定理1と同値類と商集合をわかりやすく図解～定義と具体例4つ～の議論から従います。
剰余集合(左剰余集合・右剰余集合)の具体例
剰余類の具体例と対応して，剰余集合の具体例も挙げましょう。
剰余集合の例1.
3\mathbb{Z}\subset \mathbb{Z} を和(加法)に関する部分群と見ると，
\color{red}\mathbb{Z}/3\mathbb{Z} =\{ 3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z}\}
である。
剰余集合の例2.
S_3 を 3 次対称群とし， H=\{ e, (12)\} をその部分群とする。このとき，
\color{red}\begin{aligned} G/H &= \{ H, (13)H ,(23)H \}\\ H\backslash G &=\{ H, H(13), H(23)\} \end{aligned}
はそれぞれ左剰余集合・右剰余集合である。また， A_3=\{ e, (123), (132)\} を 3 次交代群とすると，
はそれぞれ左剰余集合・右剰余集合である。特に (12)A_3=A_3(12) であったから， S_3/A_3 = A_3\backslash S_3 である。
左剰余集合と右剰余集合は濃度が一致する
次の定理は，部分群の指数を定義するにあたって基本的なものです。
定理3（左剰余集合と右剰余集合の濃度が一致）
G を群， H\subset G をその部分群とする。このとき，左剰余集合 G/H と右剰余集合 H\backslash G の濃度(要素の個数)は一致する。すなわち，
\color{red}\large | G/H | = |H\backslash G|.証明
f\colon G/H \ni gH \mapsto Hg^{-1} \in H\backslash G は全単射であることを示す。
まず，定理1の(1)式と(2)式を順番に用いることで，
\begin{aligned} g_1H=g_2H &\iff g_1^{-1} g_2 \in H \\&\iff Hg_1^{-1}=Hg_2^{-1}\end{aligned}
である。よって f は well-defined であり，さらに単射もわかる。
g\mapsto gH\mapsto Hg^{-1} は全射より， f は全射でもある。
証明終
部分群の指数
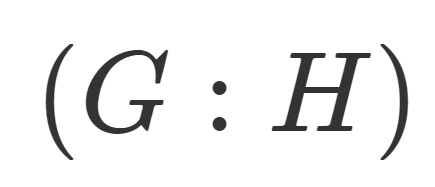
定理3より，左剰余集合・右剰余集合の濃度をもってして，部分群の指数が定義されます。
定義3（部分群の指数）
G を群， H\subset G をその部分群とする。(左・右)剰余集合の濃度(要素の個数)を \color{red} (G:H) または \color{red}[G:H] または \color{red}|G: H| などとかき，部分群 H\subset G の指数 (index) という。
剰余類の具体例・剰余集合の具体例と対応して，部分群の指数の具体例も挙げましょう。
部分群の指数の例1.
3\mathbb{Z}\subset \mathbb{Z} を和(加法)に関する部分群と見ると，
\mathbb{Z}/3\mathbb{Z} =\{ 3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z}\}
であるから， \color{red}(\mathbb{Z}:3\mathbb{Z})=3 である。
部分群の指数の例2.
S_3 を 3 次対称群とし， H=\{ e, (12)\} をその部分群とする。このとき，
\begin{aligned} G/H &= \{ H, (13)H ,(23)H \}\\ H\backslash G &=\{ H, H(13), H(23)\} \end{aligned}
であったから， \color{red} (G:H) = 3 である。また， A_3=\{ e, (123), (132)\} を 3 次交代群とすると，
であったから， \color{red} (S_3:A_3)=2 である。
という関係があることが知られています。これをラグランジュの定理 (Lagrange’s theorem) といいます。ラグランジュの定理については，以下で解説しています。（本記事を理解していれば簡単です。）
さらに進んだ話題～剰余群～
gH = Hg のとき，すなわち任意の g\in G について左剰余集合と右剰余集合が一致するとき， H を正規部分群 (normal subgroup) といいます。このとき，剰余集合も再び群と思えることが知られています。これを剰余群 (商群; quotient set) といいます。
群論において，剰余群の考えは非常に重要です。これについては，以下で解説しています。
