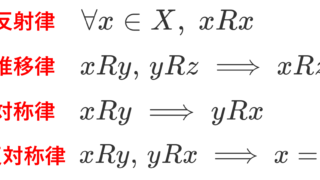同値関係とは,二項関係 \sim のうち,
- x\sim x
- x\sim y, y\sim z \implies x\sim z
- x\sim y \implies y\sim x
の3つを指すものをいいます。これについて,定義と重要な具体例5つを,順に紹介しましょう。
同値関係の定義
定義(同値関係)
X 上の二項関係 \sim が
- 任意の x\in X に対して, x\sim x (反射律)
- x,y,z\in X に対して, x\sim y, \, y\sim z ならば x\sim z (推移律)
- x,y\in X に対して, x\sim y ならば y\sim x (対称律)
をみたすとき,二項関係 \sim を同値関係 (equivalence relation) という。

二項関係のうち,3つの特別な性質をみたすものを「同値関係」というのですね。一般の同値関係には, \sim がよく使われますが,状況に応じて異なる記号を使うこともあります。
同値関係とは,「同じもの」と思える元たちの関係といえます。とりあえず具体例を見ていきましょう。
同値関係の重要な具体例5つ
教養数学や,専門数学の初歩で主に扱う,重要な同値関係の例を確認していきましょう。
例1.
m\ge 2 を整数とする。整数全体の集合 \mathbb{Z} に対して, m を法とする合同関係 \equiv \pmod m は,同値関係である。
x,y,z\in\mathbb{Z} に対して, x\equiv x \pmod m だし, x\equiv y,\, y\equiv z \implies x\equiv z \pmod m だし, x\equiv y \implies y\equiv x \pmod m でもありますね。よって同値関係です。
上の例が,同値関係のうちもっとも典型的なものと言えるでしょう。 m で割った余りに着目すると,同じものと思える関係が同値関係です。他に,三角形の合同関係も同様に同値関係であることが分かります。
別の例も見てみましょう。以下で, S^1=\{ (x,y)\in\mathbb{R}^2\mid x^2+y^2=1\} を単位円とします。
例2.
f\colon \mathbb{R}\to S^1 を f(x)=(\cos x, \sin x) と定義し, x,y\in \mathbb{R} に対して,
x\sim y \stackrel{\mathrm{def}}{\iff} f(x)=f(y)
と定めると,これは同値関係である。
ですから,同値関係であることは順番に確認可能ですね。これも,いろいろな場面で用いられる重要な同値関係です。
例3.
実数係数1変数多項式全体の集合 \mathbb{R}[X] を X^2+1 で割ったあまりで等しいものを合同と考える二項関係,すなわち,
f\equiv g \pmod{(X^2+1)} \stackrel{\mathrm{def}}{\iff} f-g は X^2+1 で割り切れる
とすると,これは同値関係である。
代数学でよく考えられる同値関係の1つです。同値関係であることの確認は,整数の余りを扱った例1.とほぼ同じですから,省略します。
次の例は,集合の濃度に関するものです。「集合の濃度」が分からない場合,読み飛ばしても差し支えありません。簡単に言うと,「2つの集合の濃度が等しい」とは,間に全単射が存在することです。
例4.
とある集合族(集合の集まり)に対し,その上の集合において,濃度が等しい」という関係は同値関係である。
集合 A に対し,その濃度を |A| とかくことにすると, |A|=|A|,\; |A|=|B|, |B|=|C|\implies |A|=|C|,\; |A|=|B| \implies |B|=|A| であることは,定義に戻って全単射の存在により分かります。よって,同値関係です。
次はベクトル空間の例を挙げましょう。ベクトル空間が分からない場合,読み飛ばしても差し支えありません。
例5.
V,W をベクトル空間, f\colon V\to W を線形写像とする。 f の核(Ker)を \operatorname{Ker} f = \{ v\in V\mid f(v)=0\} とかくことにすると, v_1,v_2\in V について,
v_1 \sim v_2 \stackrel{\mathrm{def}}{\iff} v_1-v_2\in \operatorname{Ker} f
と定めることで, \sim は V 上の同値関係となる。
これは, \sim の定義に照らすと, v\in V なら, f(v-v)=f(0)=0 なので, v\sim v ですし, v_1\sim v_2, v_2\sim v_3 を仮定すると,
\begin{aligned}f(v_1-v_3)&=f((v_1-v_2)+(v_2-v_3))\\&=f(v_1-v_2)+f(v_2+v_3)\\&=0 \end{aligned}
ですから, v_1\sim v_3 も言えます。 v_1\sim v_2\implies v_2\sim v_1 も分かりますから,同値関係になります。
これは,「準同型定理」という定理の基にもなっている重要な同値関係です。
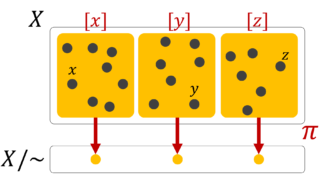
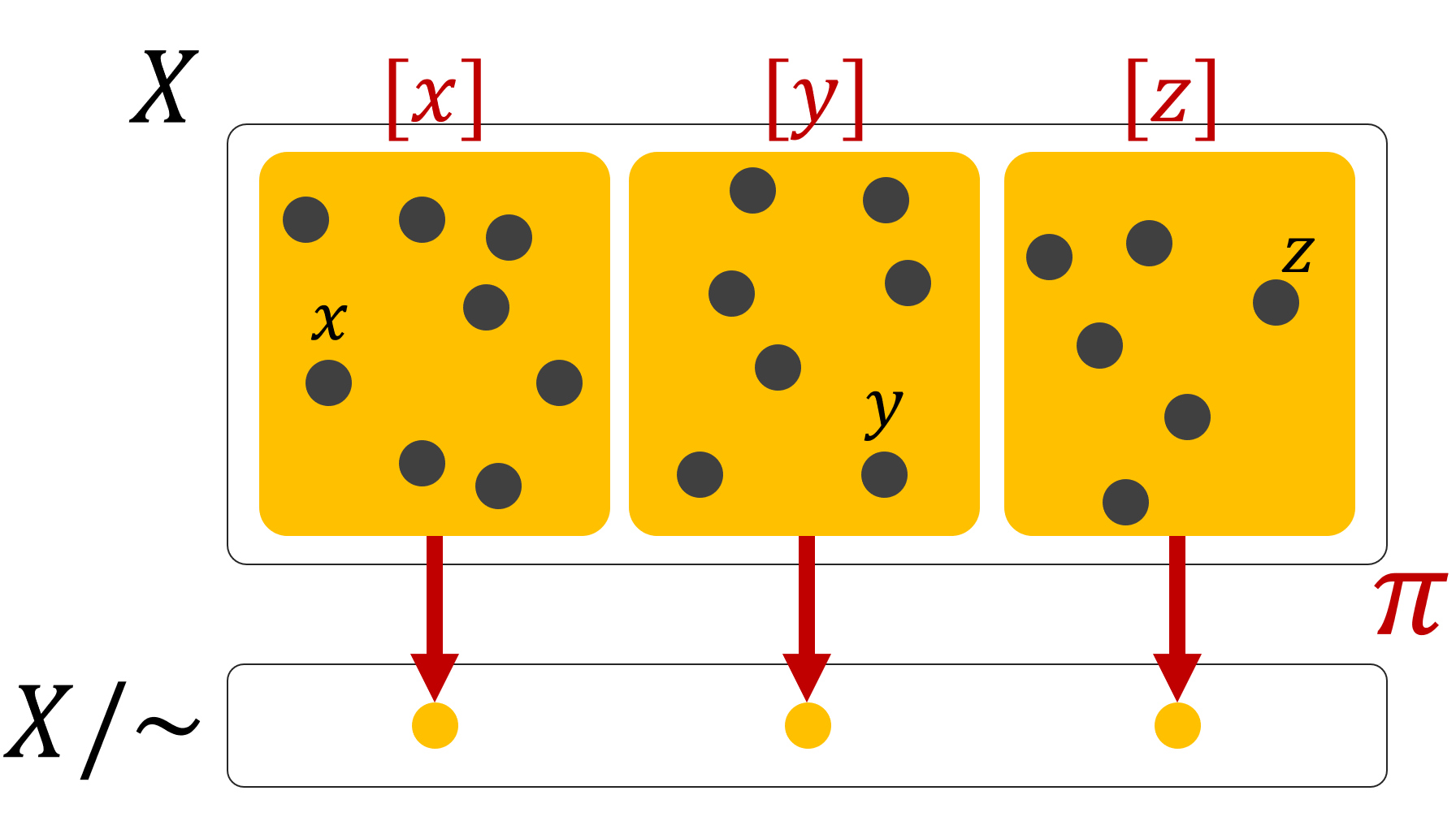
同値類と商集合
定義の直後で,同値関係は,同じものと思える元たちの関係と述べました。この考え方は「同値類」と呼ばれるもので,さらなる発展があります。これについては,以下で解説しています。