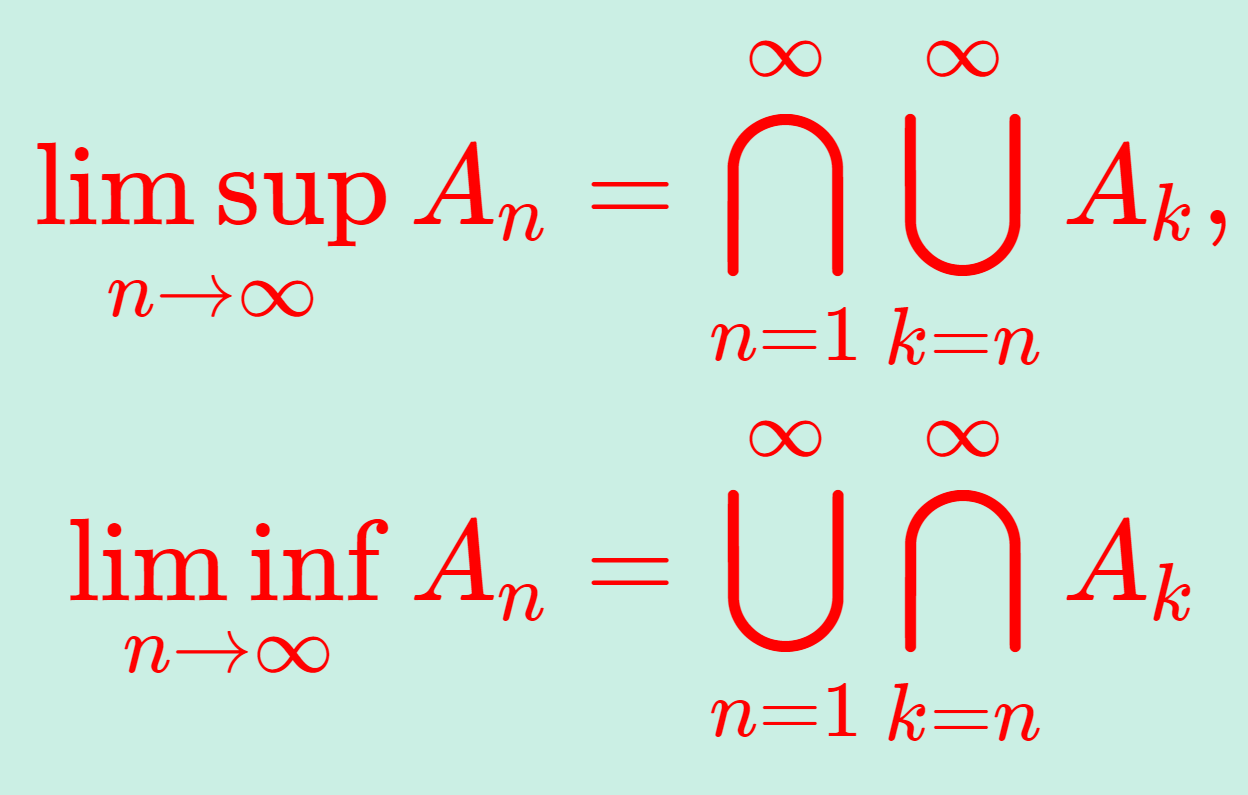無限個の集合に対して定義される2つの極限集合について考えます。
上極限集合・下極限集合・極限集合の定義
定義(上極限集合・下極限集合・極限集合)
集合列 \{A_n\} に対し,
\color{red}\begin{gathered} \limsup_{n\to\infty} A_n =\bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k, \\ \liminf_{n\to\infty} A_n = \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k \end{gathered}
をそれぞれ上極限集合 (limit superior set),下極限集合 (limit inferior set) という。
また,この両者が一致するとき,それを \color{red} \lim_{n\to\infty} A_n とかき,これを極限集合 (limit set) という。
なお本記事では, \displaystyle \limsup_{n\to\infty} A_n , \liminf_{n\to\infty} A_n と書くより, \displaystyle \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k, \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k と書いた方が分かりやすいため,基本的にはそうします(個人的には, \limsup, \liminf と書く書き方はあまり見たことがありません)。
上極限集合・下極限集合の意味
さて,上極限集合と下極限集合がどんな集合かについて,その意味を考えてみましょう。
ものすごく簡単に言うと,集合を言葉に変えるときは,前から順番に, \bigcap を「任意の」に変え, \bigcup を「ある~~が存在して」に変えればよいです。
このことを踏まえて,上極限集合 \displaystyle a \in \textcolor{red}{\bigcap_{n=1}^\infty} \textcolor{blue}{\bigcup_{k=n}^\infty} A_k を機械的に言葉に変換すると,
任意の n\ge 1 に対して,ある \color{blue}k \ge n が存在して, a \in A_k
を意味します。「 a \in A_k となる k がいくらでも大きくとれる」ということですね。これはさらに換言すると,a \in A_k となる k が無限個あることを意味します。
一方で,下極限集合 \displaystyle a \in \textcolor{blue}{\bigcup_{n=1}^\infty} \textcolor{red}{\bigcap_{k=n}^\infty} A_k を機械的に言葉に変換すると,
ある \color{blue}n \ge 1 が存在して,任意の k \ge n に対して, a \in A_k
となります。「ある一定以上の k について,それ以上では必ず a \in A_k になる」ということですね。これはさらに換言すると, a \notin A_k となる k は有限個しかないことを意味します。
以上をまとめてみましょう。
- 上極限集合 \displaystyle {\bigcap_{n=1}^\infty} {\bigcup_{k=n}^\infty} A_k は,無限個の A_k に属する元全体の集合である。
- 下極限集合 \displaystyle {\bigcup_{n=1}^\infty} {\bigcap_{k=n}^\infty} A_k は, A_k に属さない k が有限個しかない元全体の集合である。
上極限集合と下極限集合の包含関係
さて,両者の意味を考えてみると,上極限集合は単に無限個の A_k に属していればよかった(属さないものも無限個あってもよい)のに対し,下極限集合は A_k に属さないものが有限個しかないわけですから,上極限集合は下極限集合より大きい集合になることが予想されるでしょう。これが以下の主張です。
上極限集合 ⊃ 下極限集合
定理( \limsup_{n\to\infty} A_n \supset \liminf_{n\to\infty} A_n)
\color{red} \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k \supset \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k
である。
証明しましょう。
上極限集合 ⊃ 下極限集合の証明
証明
\displaystyle a \in \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k とする。
このとき,ある N \ge 1 が存在し, \displaystyle a \in \bigcap_{k=N}^\infty A_k となる。
ここで,任意の K \ge 1 に対し,
\bigcap_{k=N}^\infty A_k \subset A_{\max\{N, K\}} \subset \bigcup_{k=K}^\infty A_k
であるから,特に任意の K \ge 1 に対して, \displaystyle a \in \bigcup_{k=K}^\infty A_k となる。これは, \displaystyle a \in \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k を意味し,証明が終わる。
証明終
等号は必ずしも成立しない
さて, \displaystyle \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k \supset \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k であっても, \displaystyle \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k = \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k となるとは限りません。実際の例を確認してみましょう。
等号が成立しない例
A_n = [0, 2+(-1)^n ] と定めると,
\begin{aligned} \limsup_{n\to\infty} A_n &= \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty [0, 2+(-1)^n ] \\ &= \bigcap_{n=1}^\infty [0, 3] \\ &= [0, 3 ] \end{aligned}であるのに対し,
\begin{aligned} \liminf_{n\to\infty}A_n &= \bigcup_{n=1}^\infty \bigcap_{k=n}[0, 2+(-1)^n ] \\ &= \bigcup_{n=1}^\infty [0, 1] \\ &= [0,1] \end{aligned}
となるから,等号は成立しない。
言葉の意味で考えても,上極限集合が [0, 3] であり,下極限集合が [0,1] となることは確認できるでしょう。
極限集合が存在する十分条件
それでは,どのようなときに \displaystyle \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k = \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k が成立するのか,すなわち極限集合が存在するのかということは,興味のあるところでしょう。これについては,以下を紹介しておきます。
上極限集合と下極限集合が一致する十分条件
定理(極限集合が存在する十分条件)
- A_1 \subset A_2 \subset A_3 \subset \cdots のとき,または
- A_1 \supset A_2 \supset A_3 \supset \cdots のとき,
である。すなわち,極限集合 \lim_{n\to\infty} A_n が存在する。
証明
証明
A_1 \subset A_2 \subset A_3 \subset \cdots のとき
\begin{aligned} \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k &= \bigcap_{n=1}^\infty \bigcup_{k=1}^\infty A_k \\ &= \bigcup_{k=1}^\infty A_k \\ &= \bigcup_{k=1}^\infty \bigcap_{l=k}^\infty A_l \end{aligned}
より,等号が成立する。
A_1 \supset A_2 \supset A_3 \supset \cdots のとき
\begin{aligned} \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k &= \bigcap_{n=1}^\infty A_n \\ &= \bigcap_{n=l}^\infty A_n \text{ for all } l \ge 1\\ &= \bigcup_{l=1}^\infty \bigcap_{n=l}^\infty A_n \end{aligned}
であるから,等号が成立する。
証明終
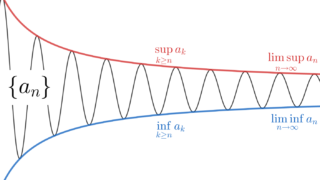
数列の極限との比較
これまで極限集合にまつわるいろいろな性質を述べました。これらについて,数列の極限と比較すると,以下のような関係があります。
| 数列 | 集合列 |
|---|---|
| \displaystyle\limsup_{n\to\infty} a_n \ge \liminf_{n\to\infty} a_n | \displaystyle \limsup_{n\to\infty} A_n \supset \liminf_{n\to\infty} A_n |
| 両辺が等しいとき, \displaystyle \lim_{n\to\infty} a_n が定義される | 両辺が等しいとき, \displaystyle \lim_{n\to\infty} A_n が定義される |
| a_1 \le a_2 \le \cdots または a_1 \ge a_2 \ge \cdots のとき極限が存在 | A_1 \subset A_2 \subset \cdots または A_1 \supset A_2 \supset \cdots のとき極限が存在 |
\le と \subset , \ge と \supset が対応していることが分かると思います。数列と集合列の極限は,類似のものであると言えますね。