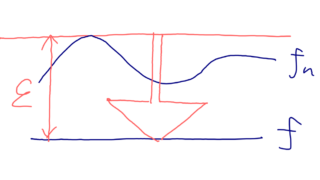
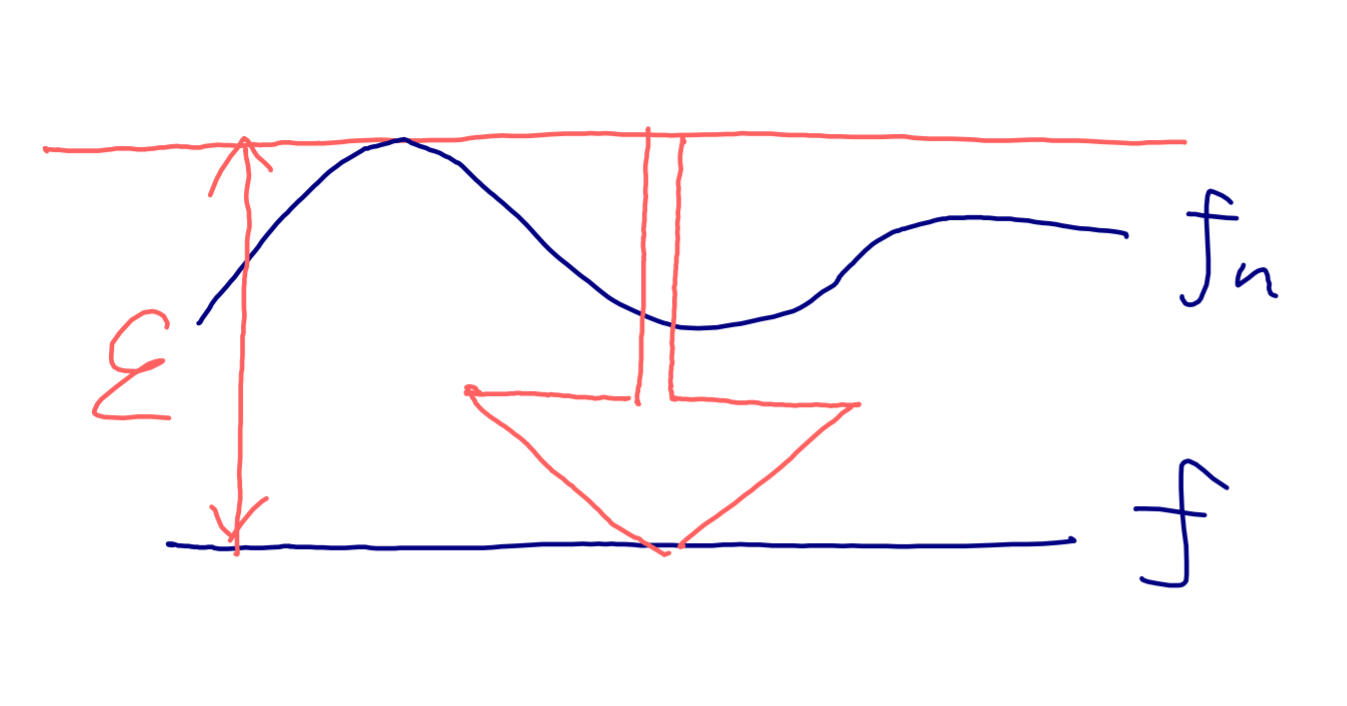
関数列の収束について，一様収束すれば各点収束することが従います。一方で，一般的に逆は成り立たず，一様収束は各点収束よりもかなり強い収束として知られています。
しかし，各点収束にある条件を加えると，一様収束が言える「ディニの定理 (Dini’s theorem) 」と呼ばれる定理があります。これを紹介しましょう。
「各点収束」と「一様収束」の違いは，以下の記事を参照してください。
ディニの定理の主張
定理（ディニ; Dini）
[0,1] 上で定義された連続関数の列 \{f_n\} が f_n(x) \le f_{n+1}(x), \,(x\in [0,1], n\ge1) をみたし，かつ連続関数 f に各点収束するとき，この収束は一様収束である。
ここでポイントなのは次の3点です。
- 関数列 \{f_n\} は連続関数であること
→ f_n(x)= \begin{cases}-1 & 0<x<1/n,\\ 0 & x=0, x\ge 1/n\end{cases} とすると， f(x)=0 に各点収束しますが，一様収束ではありません。 - f_n(x)\le f_{n+1}(x) をみたすこと
→ 以下のような f_n だと， f(x)=0 に各点収束しますが，一様収束ではありません。
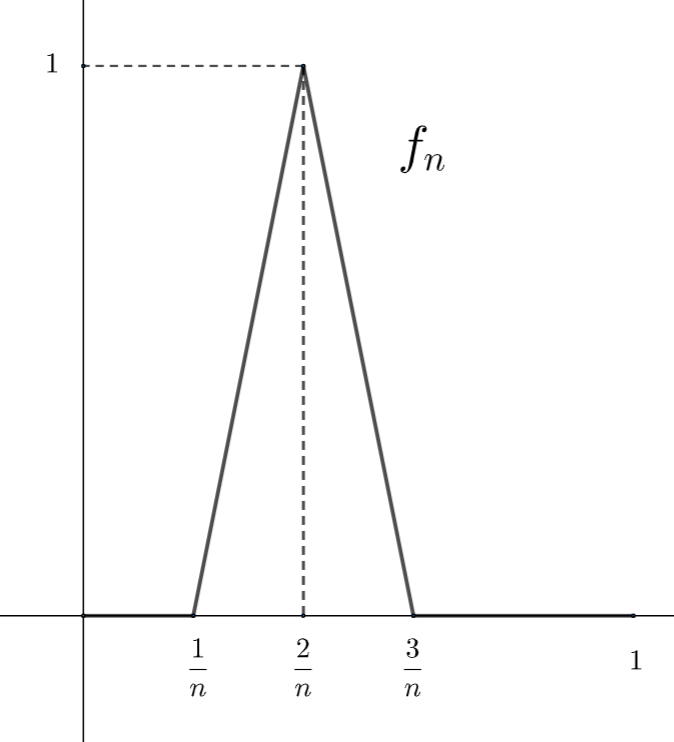
- 各点収束先は連続関数であること
→ たとえば， f_n(x)=-x^n は [0,1] 上で f(x)=\begin{cases} 0 & 0\le x<1 ,\\-1 & x=1\end{cases} に収束しますが， f は連続関数でなく，一様収束にはなりません。
また今回は関数の定義域を [0,1] としましたが，本定理は，コンパクトハウスドルフ空間上の実連続関数でも成立します。
ディニの定理の証明
証明の理解には，位相空間論の知識が必要です。
証明
\varepsilon > 0 とし，
A_n = \{ x \in [0,1] \mid f(x) - f_n(x) < \varepsilon \}
と定める。 A_n は開集合で， A_n \subset A_{n+1} \,(n\ge1), \bigcup_{n=1}^\infty A_n = [0,1] をみたすので， \{A_n\} は開被覆となる。
よって， [0,1] のコンパクト性より，有限部分被覆が存在する。 A_n の包含関係より，これは，ある N が存在して， A_N = [0,1] となることを意味する。すなわち， n \ge N に対して，
| f(x) - f_n(x) | < \varepsilon \quad (x \in [0,1])
が成立するので，一様収束が言えた。
証明終
位相空間の知識がない場合，証明は難しいですが，定理の内容だけでも理解していただければ幸いです。
類似の定理
各点収束から一様収束が従う定理としては，以下も知られています。参照してみてください。
