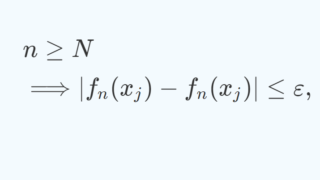アスコリ–アルツェラの定理(またはアルツェラ–アスコリの定理, Ascoli–Arzelà Theorem)は,解析学でよく使われる定理の一つですが,出てくる用語の定義が少し難しく,さらに適用条件にも注意が必要です。まず用語を確認してから,定理の主張や注意点,定理の証明へといきましょう。
一様有界と同程度連続性
定義(一様有界・同程度連続)
関数列 \{f_n\} は定義域が区間 [a,b] である連続関数の列とする( -\infty < a < b < \infty )。
関数列 \{f_n\} が一様有界 (uniformly bounded) であるとは,(n,x に依存しない) K>0 が存在して,
|f_n(x)| < K \quad n\ge1, x\in [a,b]
が成立することである。
また,関数列 \{f_n\} が同程度連続(同等連続, equi-continuous) であるとは,任意の \varepsilon >0 に対し,ある \delta > 0 が存在して,任意の n に対して
|x-y| < \delta \Rightarrow |f_n(x) - f_n(y) | < \varepsilon
が成立することである。
要するに「一様有界」とは,各関数 f_n 有界であるのはもちろん, どの n に対しても「同じくらい」有界( n を増やすたびに |f_n| が段々 \infty に行ったりしない)だといえるでしょう。
「同程度連続」とは,各関数 f_n が連続(一様連続)であるのはもちろん, どの n に対しても「同じくらい」連続 ( n を増やすたびに f_n の”傾き”が段々急になったりしない)だといえるでしょう。
準備は整いました。定理の主張に入っていきましょう。
アスコリ–アルツェラの定理
定理(アスコリ–アルツェラ; Ascoli–Arzelà)
関数列 \{f_n\} は定義域が区間 [a,b] である連続関数の列とする( -\infty < a < b < \infty )。この関数列が一様有界かつ同程度連続であるならば,一様収束する部分列が存在する。
定理自体は難しくないように見えるかもしれませんが,適用条件が比較的難しく,正しく使えないことが多い定理だと思います。注意点は以下の2点です。
1つめは, \mathbb{R} 上でもほぼ同じことが言えますが,「アスコリ–アルツェラの定理」と言ったときには有界区間で使うほうが無難でしょう。
2つめは, L^2 収束など,別の収束を習った数学徒向けのメッセージです。
アスコリ–アルツェラの定理の証明
証明には,対角線論法 (diagonal argument) といわれる,重要な技法を使います。
証明
有理数を適当な順番に並べたものを \{x_i\} とする。一様有界性より,数列 \{f_n(x_1)\} は有界であるから,ボルツァノ–ワイエルシュトラス (Bolzano–Weierstrass) の定理より,収束部分列 \{f^{(1)}_n\}_{n=1}^\infty \subset \{f_n\}_{n=1}^\infty が存在する(下の添え字は付け直した)。
同様に今度は数列 \{f^{(1)}_n(x_2)\} の有界性から,収束部分列 \{f^{(2)}_n\}_{n=1}^\infty \subset \{f^{(1)}_n\}_{n=1}^\infty が存在する。
同様の操作を何度も繰り返すことで, \{f^{(k)}_n\}\,(k\ge 1) を得る。
ここで, \{f^{(n)}_n\}_{n=1}^\infty を考えよう(対角線論法)。すべての有理数 x_i において \{f^{(n)}_n(x_i)\}_{n=1}^\infty は極限を持つことに注意する。
\varepsilon > 0 としよう。同程度連続性により,
|x-y| < \delta \Rightarrow |f_n^{(n)} (x) - f_n^{(n)} (y) |< \varepsilon
となる n によらない \delta > 0 がとれる。
ここで, a \le q_1 < q_2 < \ldots <q_l \le b となる q_1, q_2 , \ldots ,q_l \in \mathbb{Q} を
q_1 - a, q_{j+1} - q_j, b-q_l < \delta \quad (1\le j \le l-1)
となるようにとる。
\{f^{(n)}_n(q_j)\}\,(1\le j\le l) は極限を持つので,ある N \ge 1が存在して,任意の 1\le j \le l に対し,
m,n > N \Rightarrow |f^{(m)}_m(q_j) - f^{(n)}_n(q_j) | < \varepsilon.
s \in [a,b] とする。このとき, |s-q_j| < \delta となる q_j が選べる。 m,n > N とするとき,
\begin{aligned}
&|f^{(m)}_m(s) - f^{(n)}_n(s)| \\
\le& |f^{(m)}_m(s) - f^{(m)}_m(q_j)| \\
&+ |f^{(m)}_m(q_j) - f^{(n)}_n(q_j)| \\
&+ |f^{(n)}_n(q_j) - f^{(n)}_n(s)| \\
\le& \varepsilon + \varepsilon + \varepsilon = 3\varepsilon.
\end{aligned}
よって \{f^{(n)}_n\} は一様コーシー列であり,一様収束する。
証明終
位相空間論におけるアスコリ–アルツェラの定理
より一般的なアスコリ–アルツェラの定理を述べておきましょう。
定理(アスコリ–アルツェラ; Ascoli–Arzelà,一般型)
X をコンパクトハウスドルフ空間とし,その上の連続関数の空間 C(X) には一様収束位相が入っているとする。
このとき, S \subset C(X) が相対コンパクトであることの必要十分条件は S が一様有界かつ同程度連続であることである。
必要十分条件であることがポイントです。証明はたとえば,以下の参考文献の定理29.3を参照してください。
補足~各点収束+同程度連続 = 一様収束~
アスコリ-アルツェラの定理の証明でも使った三角不等式のテクニックを使うことにより,以下が従います。
定理
\{f_n\} を [a, b ] 上同程度連続な関数列とし, f \colon [a, b] \to \mathbb{R} に各点収束するとする。
このとき,この収束は一様収束である。
これ単体の証明については,以下の記事を参照してください。