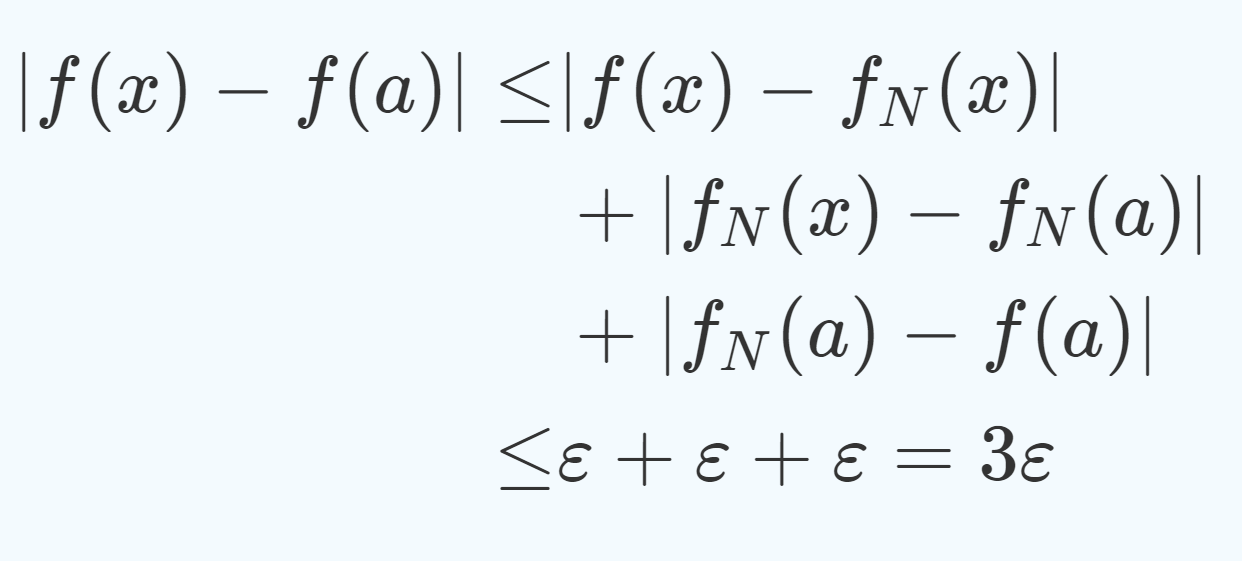一様収束 (uniformly convergence) と各点収束 (pointwise convergence) の顕著な違いとして，連続関数列の極限が再び連続関数になるという性質が挙げられます。このことの証明と，なぜ一様収束でないとこの性質が言えないのかを考えてみましょう。
一様収束と各点収束の違いは，以下の記事を参照してください。
連続関数列の一様収束極限は必ず連続関数になる
定理
\{f_n\} は [0,1] 上で定義された連続関数の列とし， f に一様収束するとする。このとき， f は [0,1] 上連続である。
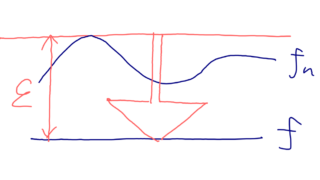
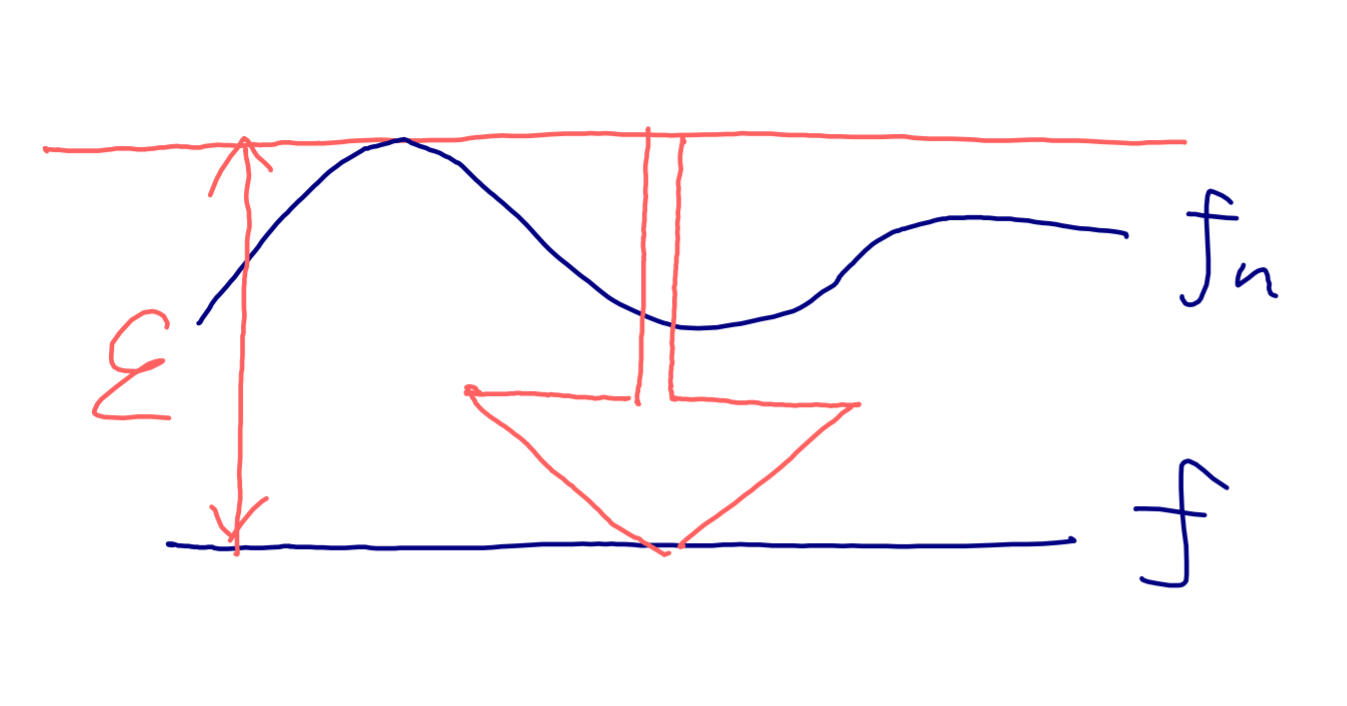
これは，各点収束では言えない，一様収束ならではの性質です。各点収束では言えない例については，たとえば，上リンク先の記事の例3を参照してください。
連続関数列の一様収束極限は必ず連続関数になることの証明
証明
\varepsilon > 0, a \in [0, 1] を固定する。
一様収束することから，ある N \ge 1 が存在して，(★)
|f_N(x) - f(x) | < \varepsilon, \quad x \in [0,1]
が成立する。 f_N は連続であるから，ある \delta > 0 が存在して，
|x-a| < \delta \Rightarrow |f_N(x) - f_N(y) | < \varepsilon
が成立する。
以上を踏まえて， x \in [0, 1] が |x-a| < \delta をみたすならば，三角不等式より，
\begin{aligned}
|f(x) - f(a) |
\le & |f(x) - f_N(x)| \\
& + |f_N(x) - f_N(a)| \\
& + |f_N(a) - f(a) | \\
\le & \varepsilon + \varepsilon + \varepsilon = 3\varepsilon
\end{aligned}
となるから， f は連続である。
証明終
さて，この証明で一様収束を用いているのはどこでしょうか。一様収束が各点収束に変わるとどこが問題になるのでしょうか。
一様収束を用いているのは，上の (★) の部分です。 |f(x) - f_N(x) | < \varepsilon が任意の x \in [0,1] について成立することがポイントです。
最後の三角不等式のところで， |x - a| < \delta をみたす任意の x \in [0,1] に対して， | f(x) - f_N(x)| < \delta であることを用いていますが，これができるのは (★) の一様収束性があるからですね。
