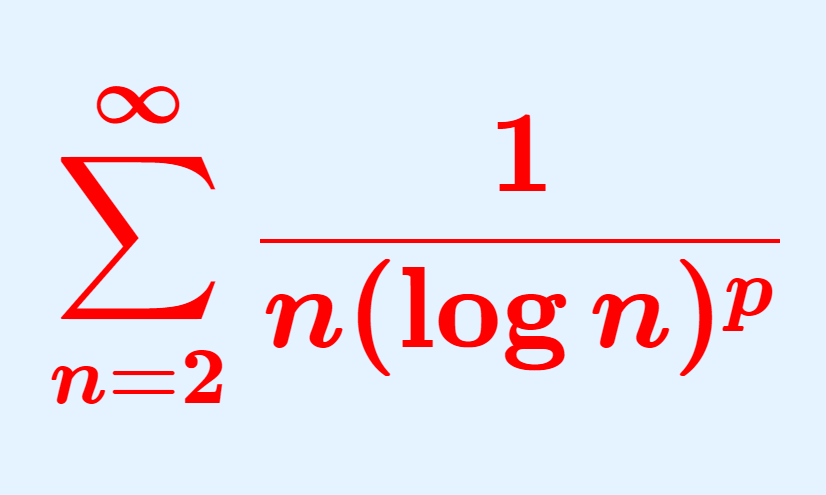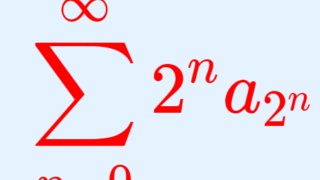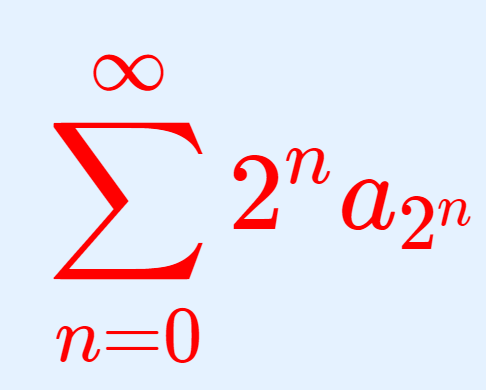\sum_{n=1}^\infty 1/n^p における収束・発散について, 0<p\le 1 で発散し, p > 1 で収束することは有名でしょう。これと同じようなことが, \sum_{n=2}^\infty 1/(n(\log n)^p) についても成り立ちます。
これについて,その定理の主張と証明を確認していきましょう。
1/nlogn型の級数の収束・発散
定理( 1/n\log n 型の級数の収束・発散)
\color{red}\boldsymbol{ \sum_{n=2}^\infty \frac{1}{n(\log n)^p } }
は,
- \color{red}\boldsymbol{0 \le p \le 1} のとき発散
- \color{red} \boldsymbol{p > 1} のとき収束
する。
定理としては非常にシンプルですね。 n \log n 分の 1 を境に,収束・発散が変わるのです。
早速証明していきましょう。
1/nlogn型の級数の収束・発散の証明
証明には, 1/n^p の収束・発散を論じたときにも用いた,広義積分による収束判定法を使います。この収束判定法について詳しくは,以下の記事を参照してください。
これを踏まえて,証明を確認していきましょう。
証明
広義積分による収束判定法により,求める級数の収束・発散は,\int_2^\infty 1/(x(\log x)^p )\, dx の収束・発散に一致する。
\begin{aligned}\int_2^\infty \frac{1}{x(\log x)^p }\, dx &=\begin{cases} \left[ \frac{(\log x)^{1-p}}{1-p} \right]_2^\infty & p \ne 1, \\ [\log \log x]_2^\infty & p =1 \end{cases} \\ & \begin{cases} = \infty & 0\le p\le 1, \\ <\infty &p > 1. \end{cases}\end{aligned}
であるから,結論が示せた。
証明終
\int_2^\infty 1/(x(\log x)^p )\, dx の積分が分かるかどうかが鍵でしたね。
なお,この収束・発散については,積分を用いずとも,Cauchy Condensation Test を用いて求めることも可能です。以下で解説しています。