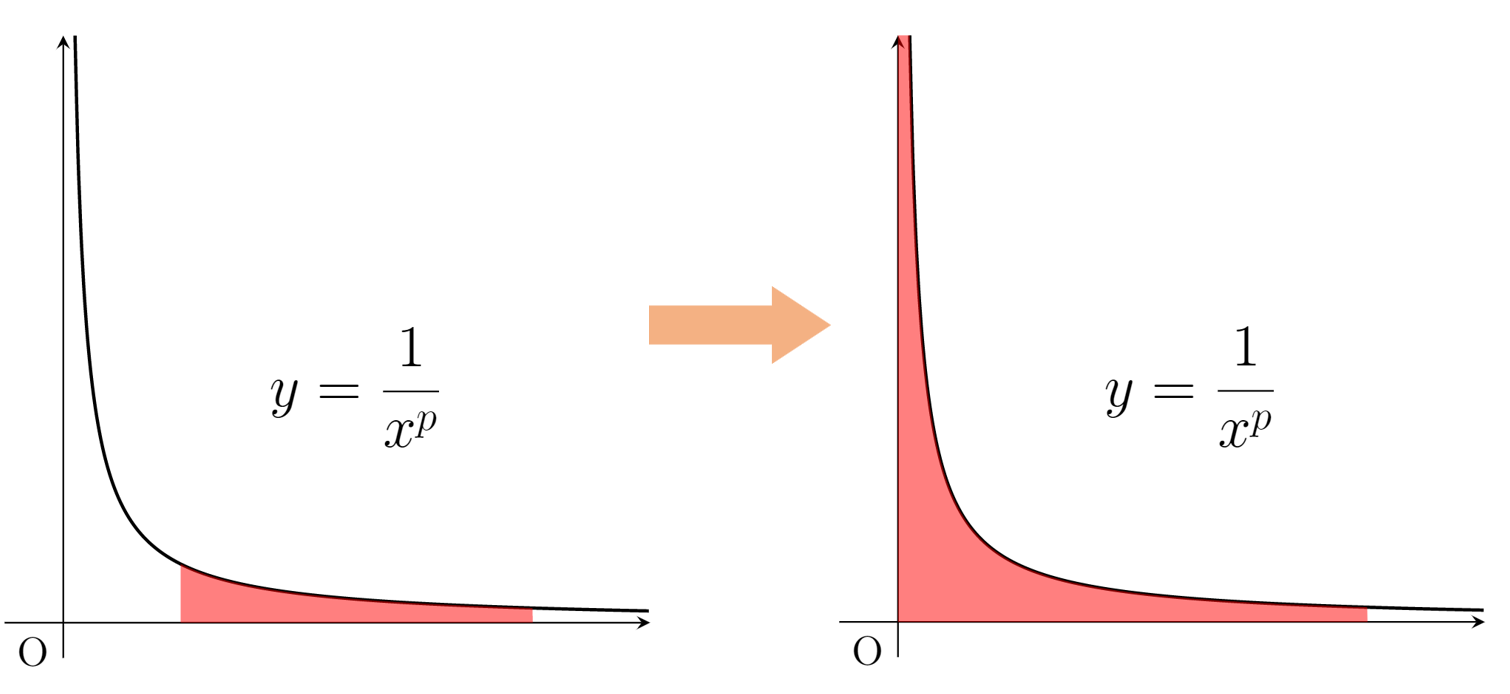
リーマン積分における広義積分(広義リーマン積分)について,その定義と具体例5つを紹介します。
広義積分の定義
そもそも,高校や大学の教養課程で習う(リーマン)積分とは,以下のようなものでした。
(詳しくは,リーマン和による定積分の定義とリーマン積分可能・不可能な例を参照してください)
これを,
- 有界な関数以外でも積分したい!
- 有界な区間以外でも積分したい!
と考えたのが広義積分です。定義を述べましょう。
定義(広義積分)
1. 非有界な関数での積分
f \colon (a, b] \to \mathbb{R} は, a の近くで有界でなく,任意の a<a' に対し, [a',b] 上有界かつ可積分であるとする。このとき,
\lim_{a'\to a+}\int_{a'}^b f(x)\, dx
が有限値に収束するならば,f は (a,b] 上広義積分可能 (improper integrable) であるといい,その極限を \displaystyle \color{red} \int_a^b f(x)\, dx とかく。
f\colon [a,b)\to\mathbb{R} で, b の近くで有界でない場合も同じである。
2. 無限区間での積分
f\colon [a,\infty) \to\mathbb{R} が,任意の a<b に対して, [a,b] 上可積分(広義でも良い)とする。このとき,
\lim_{b\to\infty} \int_a^b f(x)\, dx
が有限値に収束するならば, f は [a,\infty) 上広義積分可能 (improper integrable) であるといい,その極限を \displaystyle \color{red} \int_a^\infty f(x)\, dx とかく。
f\colon (-\infty, b] \to\mathbb{R} のときも同様である。
有界でない関数の積分,無限区間における積分を,普通の積分の極限の形で定義できましたね。
ここで注意ですが,広義積分とは,「積分を定義できる範囲で定義してから極限を取ったもの」です。リーマン和を考える,根本の部分から有界性を外したわけではないです。
あくまで「普通の有界な関数でリーマン和 → 普通の積分 → その結果を拡張して広義積分」の手順をたどっており,「拡張したリーマン和 → 広義積分」ではないわけです。
また,広義積分の記号は,積分と同じものを使われるため,判別が難しいかもしれません。「有界な関数でない」または「有界な区間でない」とき,広義積分であると思うとよいです。
広義積分の具体例5つ
定義だけでは分かりにくいと思うので,例を確認していきましょう。
有界関数でない広義積分の例
例1.
p>0 とする。このとき, 0<a<1 に対して,
\int_a^1 \frac{1}{x^p}\, dx= \begin{cases} \frac{1}{1-p}(1-a^{1-p}) & p<1, \\ -\log a & p=1, \\ \frac{1}{p-1}(\frac{1}{x^{p-1}}-1) & p>1 \end{cases}
であるから,両辺 a\to 0+ として,
よって特に, 0<p<1 のとき, (0,1] 上広義積分可能である。
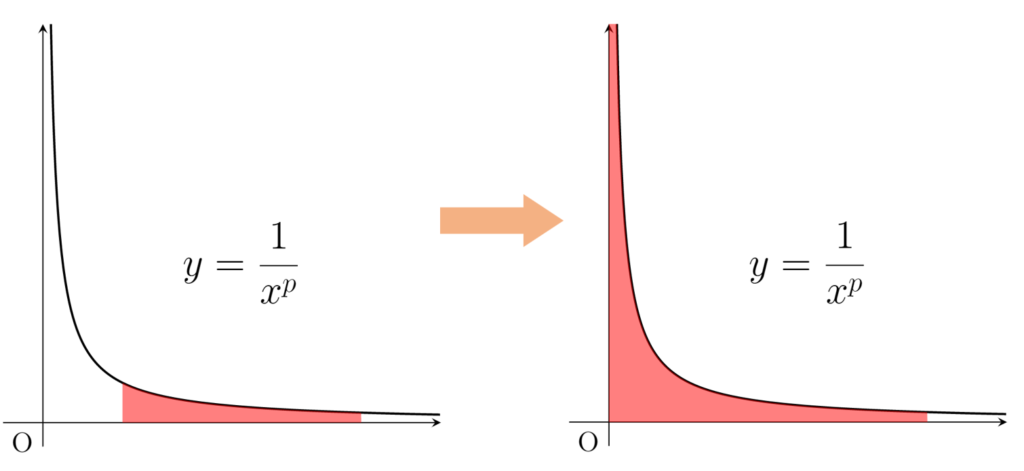
これは有名な広義積分ですから, 0<p<1 のとき, (0,1] 上広義積分可能であることを覚えましょう。
例2.
0<a<1 に対し,
\int_a^1 \log x \, dx = a(1-\log a)-1
であるから,両辺 a \to 0+ として,
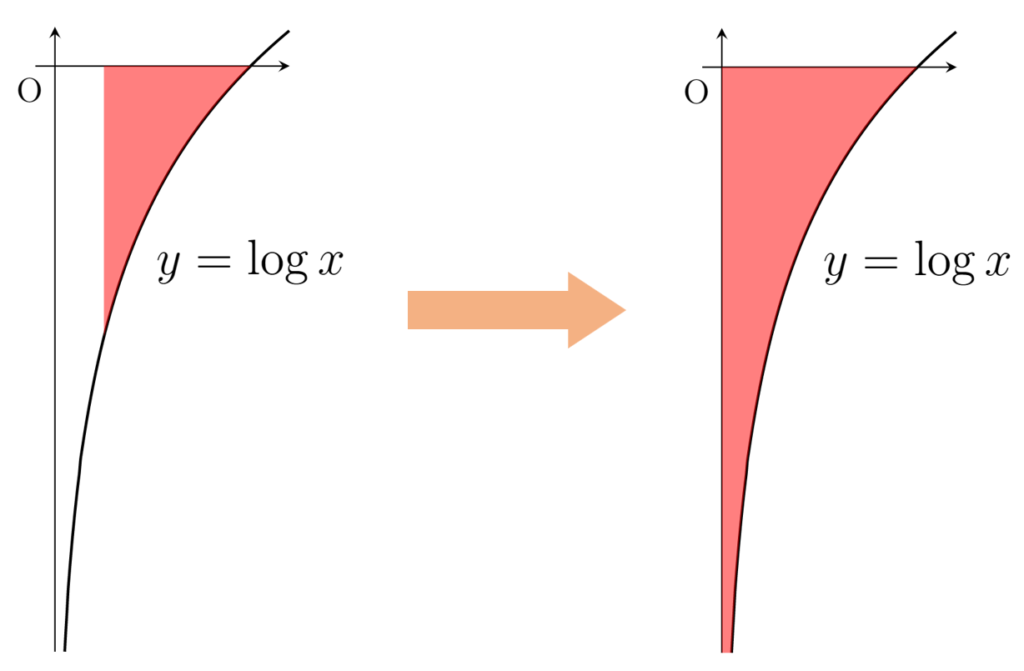
有界区間でない広義積分の例
例3.
p>0 とする。このとき, 0<a<1 に対して,
\int_1^b \frac{1}{x^p}\, dx= \begin{cases} \frac{1}{1-p}(b^{1-p}-1) & p<1, \\ \log b & p=1, \\ \frac{1}{p-1}(1-\frac{1}{b^{p-1}}) & p>1 \end{cases}
であるから,両辺 b\to \infty として,
よって特に,p>1 のとき, [1,\infty) 上広義積分可能である。
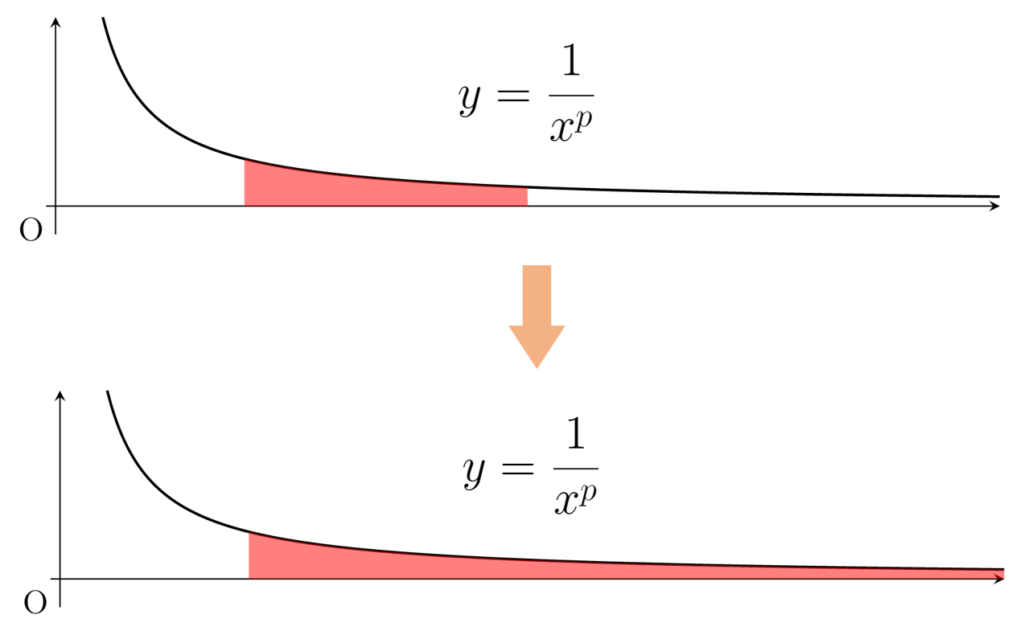
f(x) = 1/x^p に関しては,例1で, 0<p<1 のとき, (0,1] 上広義積分可能であることを確認しましたね。一方で, p>1 のときは, [1,\infty) 上広義積分可能になります。こちらも覚えましょう。
例4.
b, \lambda>0 とする。
\int_0^b e^{-\lambda x}\, dx = \frac{1}{\lambda}(1-e^{-\lambda b})
であるから,両辺 b \to\infty とすると,
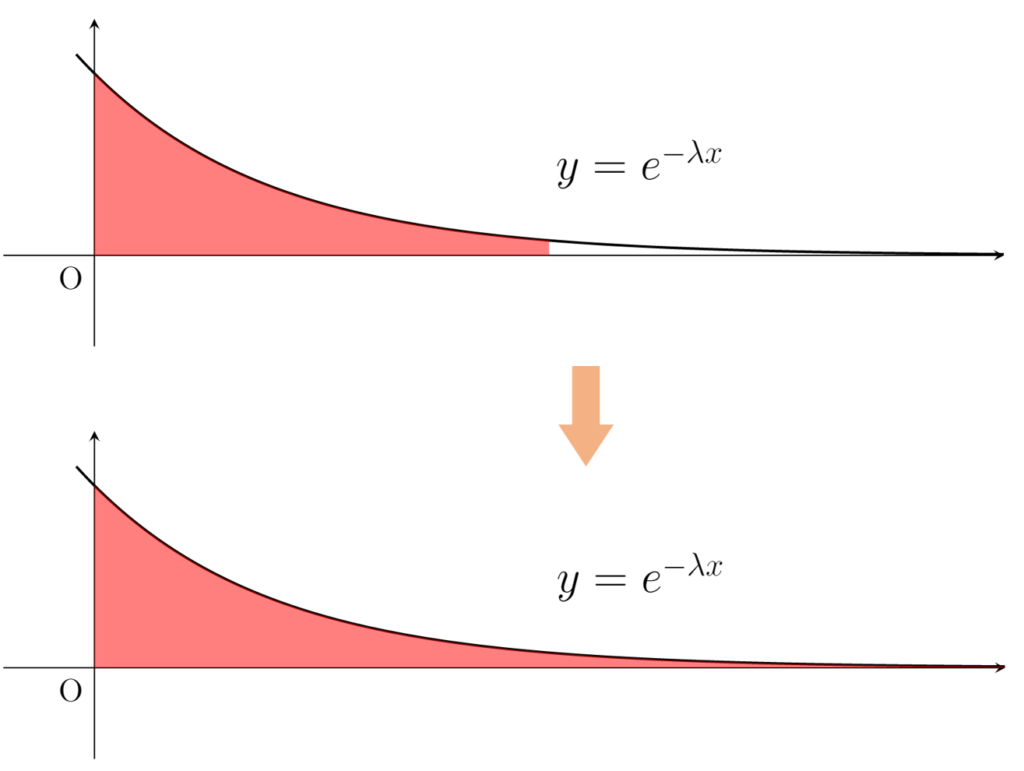
一般に,指数減衰する関数は [0,\infty) 上広義積分可能です。
例5.
f(x) =\sin x /x は [0,\infty) 上広義積分可能で,
\color{red} \int_0^\infty \frac{\sin x }{x}\, dx = \frac{\pi}{2}.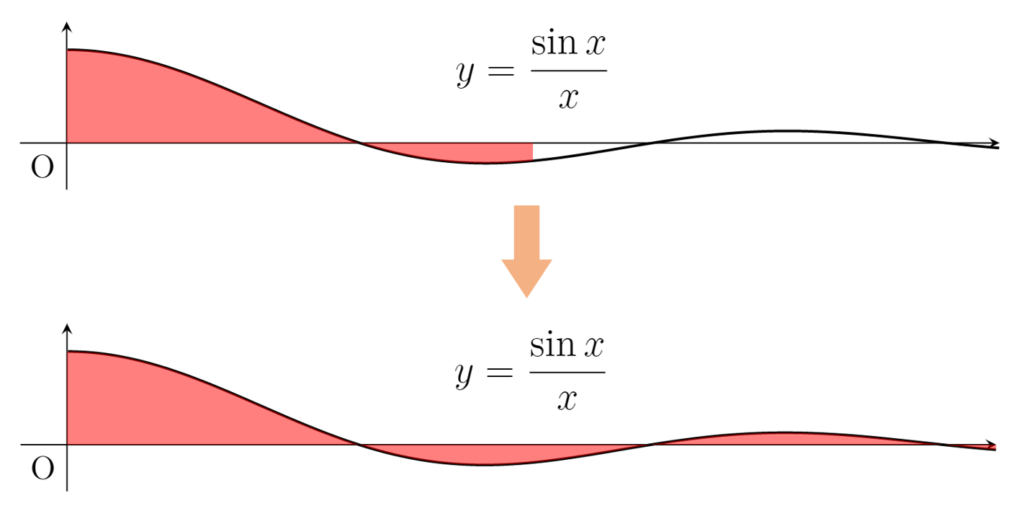
これは元の積分は収束するが, \displaystyle \int_0^\infty \left|\frac{\sin x}{x} \right|\, dx = \infty となる,有名な例です。 実際の積分方法は非常にテクニカルで,ココで紹介できるレベルを超えるので,またの機会にしましょう。
また,注意ですが, \sin x/x は 0 付近で有界なので, 0 付近で積分することは,広義積分に相当しません。
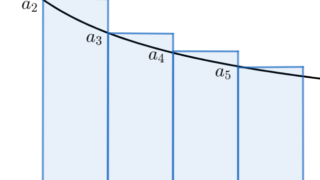
広義積分を用いた無限級数の収束判定
広義積分の応用例の一つとして,無限級数の収束判定に用いるというのがあります。これについては,以下の記事を参照してください。