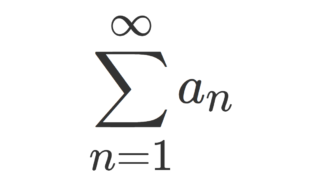【乗積級数】コーシー積とその証明～2つの無限級数の積～

コーシー積 $\displaystyle \sum_{n=0}^\infty \sum_{k=0}^n a_kb_{n-k} =\left(\sum_{n=0}^\infty a_n \right) \left(\sum_{n=0}^\infty b_n\right)$ について，その定理の主張と証明，最後に具体例を紹介しましょう。

【乗積級数】コーシー積～2つの無限級数の積～
コーシー積の証明
コーシー積の具体例
関連する記事

【乗積級数】コーシー積～2つの無限級数の積～

定理（コーシー積, Mertens）

$\displaystyle \sum_{n=0}^\infty a_n , \sum_{n=0}^\infty b_n$ がともに収束し，少なくとも一方が絶対収束するとき，

\color{red} \sum_{n=0}^\infty \sum_{k=0}^n a_kb_{n-k} =\left(\sum_{n=0}^\infty a_n \right) \left(\sum_{n=0}^\infty b_n\right)

が成り立つ。

2つの無限級数の積は，「係数の和が常に一定になるようなところ」に注目して，それを足し上げても同じになるということですね。図で描くと，以下のようなイメージです。

「係数の和が一定になるところを足す」というのを，級数の畳み込み (convolution) ということもあります。

なお，元の級数の2つともが絶対収束する場合は， $\sum_{n=0}^\infty \sum_{k=0}^n a_kb_{n-k}$ も絶対収束します。実際，

\sum_{n=0}^N \sum_{k=0}^n| a_k||b_{n-k}| \le \left(\sum_{n=0}^N |a_n| \right) \left(\sum_{n=0}^N |b_n|\right)

となることから分かります。

コーシー積の証明

証明は少しテクニカルかもしれません。やっていきましょう。

証明

$\displaystyle \sum_{n=0}^\infty a_n$ が絶対収束するとして証明しよう。このとき， $\alpha= \displaystyle \sum_{n=0}^\infty |a_n|$ とおくことにする。

\begin{gathered} A_N =\sum_{n=0}^N a_n,\, B_N = \sum_{n=0}^N b_n, \\ C_N = \sum_{n=0}^N \sum_{k=0}^n a_kb_{n-k},\\ \beta_N = B-B_N \end{gathered}

と定める。示すべきことは， $C_N \xrightarrow{N\to\infty} AB$ である。

\begin{aligned}C_N ={}& a_0b_0 \\ &+ (a_0b_1+a_1b_0) \\ &+\cdots+(a_0b_N+\dots + a_Nb_0) \\ ={}& a_0B_N+a_1B_{N-1}+\dots + a_NB_0 \\ ={}& a_0(B-\beta_N)\\ &+a_1(B-\beta_{N-1})\\ &+\dots+a_N(B-\beta_0) \\ ={}&A_NB-(a_0\beta_N+\dots +a_N\beta_0) \end{aligned}

であり， $A_NB\xrightarrow{N\to\infty} AB$ であるから， $a_0\beta_N+\dots +a_N\beta_0 \xrightarrow{N\to\infty} 0$ を示せばよい。

$\varepsilon > 0$ とする。 $\beta_N=B-B_N\xrightarrow{N\to\infty} 0$ であるから，ある $N_0 \ge 0$ が存在して，

N \ge N_0 \implies |\beta_n|\le \varepsilon

とできる。このような $N \ge N_0$ に対し，

\begin{aligned} &|a_0\beta_N+\dots +a_N\beta_0| \\ \le{}& |a_0 \beta_N + \dots + a_{N-N_0}\beta_{N_0}|\\ & + |a_{N-N_0+1}\beta_{N_0-1}+\dots+a_N\beta_0| \\ \le{}& \alpha \varepsilon + |a_{N-N_0+1}\beta_{N_0-1}+\dots+a_N\beta_0| \end{aligned}

であり，最終辺第2項は $a_N\xrightarrow{N\to\infty} 0$ より， $0$ に収束するため，

\limsup_{N\to\infty} |a_0\beta_N+\dots +a_N\beta_0| \le \alpha\varepsilon

となる。結局， $a_0\beta_N+\dots +a_N\beta_0 \xrightarrow{N\to\infty} 0$ が示せたので，証明が終わる。

証明終

コーシー積の具体例

ひとつだけ具体例を挙げましょう。

例

$\displaystyle \color{red} \left(\sum_{n=0}^\infty \frac{x^n}{n!}\right) \left(\sum_{n=0}^\infty \frac{y^n}{n!}\right) = \sum_{n=0}^\infty \frac{(x+y)^n}{n!}$ である。

これは， $e^x$ のマクローリン展開の話ですから，結局 $\color{red} e^xe^y = e^{x+y}$ と言っているに過ぎないのですが，これを確認してみましょう。

$\sum_{n=0}^\infty x^n/n!$ は任意の実数 $x$ で絶対収束することに注意すると，