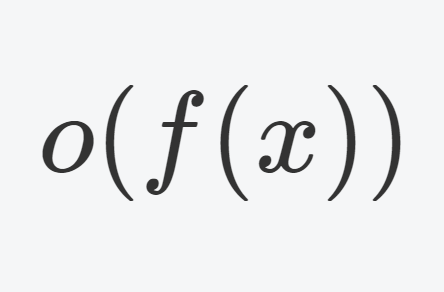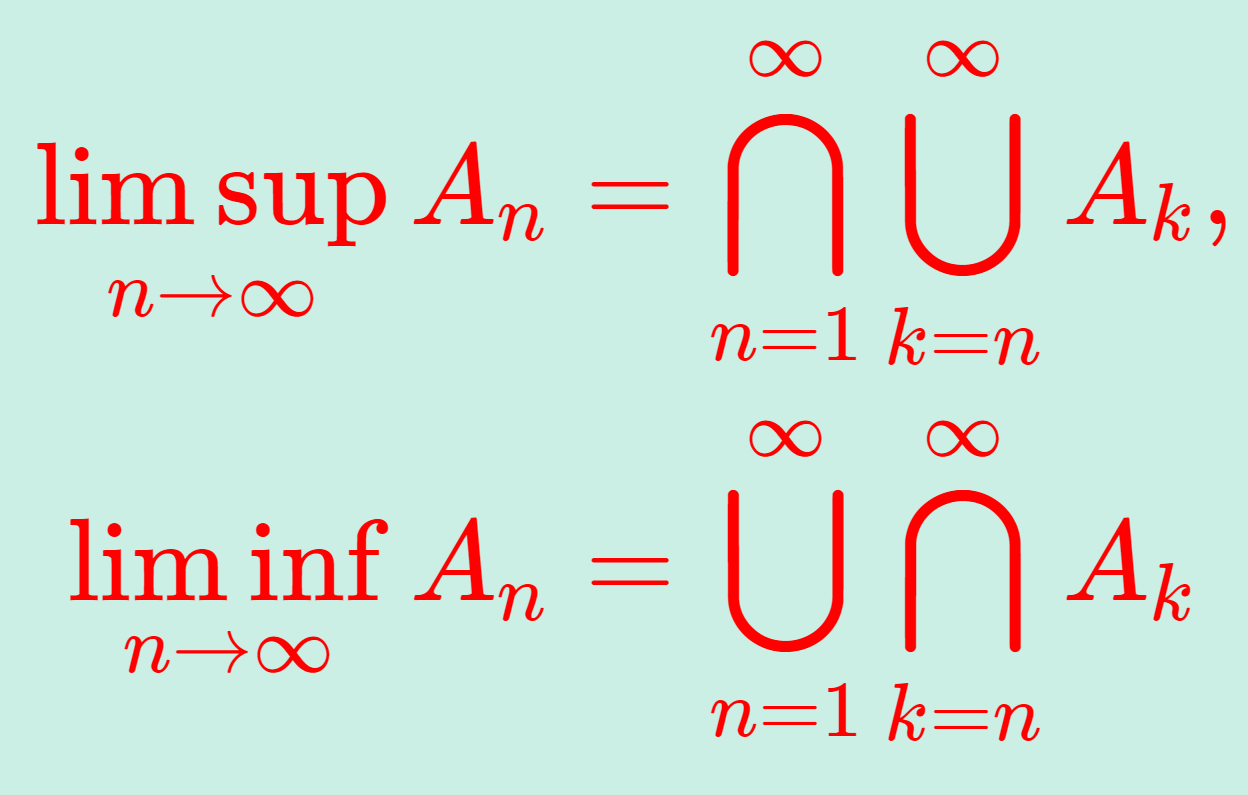収束の「オーダー」すなわち,どのくらいの速さで収束するのかということを述べるために用いられる,ランダウの記号について紹介します。
ランダウの記号の定義
定義(ランダウの記号)
-\infty \le a \le \infty とし, f(x) , g(x) を a の近くで定義されている関数とする。
a の十分近くで,ある M>0 が存在して
となるとき, \color{red} f(x) = O(g(x)) \, (x\to a) とかく。また,
となるとき, \color{red} f(x) = o(g(x)) \, (x\to a) とかく。
記号 O, o をランダウの記号 (Laudau’s notation, Big O small O notation) という。
O (ビッグオー)の定義の方は,「十分近くで」という言葉を使ってしまったので,イプシロンデルタ論法を用いて厳密に言い換えておきます。本記事単体では,あまりよく分からなくても大丈夫です。
ある M, \delta > 0 が存在して,
|x-a| < \delta \implies |f(x)| \le M |g(x)|
が成立するとき, \color{red}f(x) = O(g(x)) \, (x\to a) とかく。
a 以外の a の近くで g(x) \ne 0 が成立するとき,もっと単純に定義できます。
g は a の十分近くで g(x) \ne 0 \,\,(x\ne a) とする。
\limsup_{x\to a}\left|\frac{f(x)}{g(x)}\right| < \infty
が成立するとき, \color{red}f(x) = O(g(x)) \, (x\to a) とかく。
逆に, a の近くで g(x) = 0 が成立するとき,同じ近くで f(x) = 0 が成立するときにビッグオーの定義をみたします。しかし,正直これを考えるのは面白くないので,そもそもあまり考えることがありません。従って実際のところは,上の定義が O の定義と思っても差し支えないです。
ランダウの記号の意味と具体例
感覚的に言うと,これらは収束の速さについて比較しているものです。
f(x) \to \infty や f(x) \to 0 の場合に,同じく g(x) \to \infty や g(x) \to 0 となる関数と比較して述べられることがほとんどです。
実際,それ以外の値に収束するときを考えても,あまり面白くないです。 O, o は基本的に \lim_{x\to a} |f(x)/g(x)| を考えますから, 形式的に \infty/\infty や 0/0 に収束する場合で述べることに大きな意味があります。
これを踏まえて, f(x) \to \infty の場合と, f(x) \to 0 の場合に「意味」を考えていきましょう。
f(x) → ∞ の場合
f(x) \to\infty のとき
f(x) = O(g(x)) \, (x\to a) と書くと, f(x) は g(x) と同じくらいかまたは遅いスピードで \infty に行くことを意味します。
f(x) = o(g(x)) \, (x\to a) と書くと, f(x) は g(x) より遅いスピードで \infty に行くことを意味します。
具体例を見てください。
例1.
- 3x + 2x^3 = O(x^3) \,\, (x\to \infty).
- 3x + 2x^3 = o(x^4) \,\, (x\to\infty).
- \displaystyle \sum_{n=1}^\infty \frac{1}{x^n} = \frac{1}{x} + O \left(\frac{1}{x^2} \right)\, (x\to 0+).
- \displaystyle \sum_{n=1}^\infty \frac{1}{x^n} = \frac{1}{x} + o\left( \frac{1}{x^3}\right) \, (x\to 0+).
- \displaystyle (n+1)\log n = O(n \log n). \,\, (n\to\infty).
- f(x) \xrightarrow{x\to a} \infty, g(x) \xrightarrow{x\to a} 0 のとき, f(x) g(x) = o(f(x)) \,\, (x\to a) .
カッコ内を満たすように x を動かしたとき,すべて \infty に行くことに注意しましょう。
上以外にも,たとえば 3x+2x^3 = O(x^4) \, (x\to\infty) も正しいですが,できるだけ厳密に評価した方が良いと考えられているため,そのように書くことは基本的にありません。逆に言えば, f(x) = O(x^3) と書かれた場合は,たいていの場合,収束スピードは x^3 と「同じ」と考えてよいです。これを,収束のオーダー (order) と言います。
同じ理由で, 3x + 2x^3 = o(x^4) と書くよりも, 3x + 2x^3 = O(x^3) と書いた方が良いと考えられています。
6.は,スモールオー o の特に有用な例です。 g(x) \to 0 の収束の速さが分からない限り,ビッグオー O を用いて「厳密に」書き表すことはできません(もちろん,定義の上では f(x) g(x) = O(f(x)) も間違いでないです)。
f(x) → 0 の場合
f(x) \to 0 のとき
f(x) = O(g(x)) \, (x\to a) と書くと, f(x) は g(x) と同じくらいかまたは速いスピードで 0 に行くことを意味します。
f(x) = o(g(x)) \, (x\to a) と書くと, f(x) は g(x) より速いスピードで 0 に行くことを意味します。
具体例を見てください。
例2.
- 3x+2x^3 = O(x) \,\, (x\to 0).
- 3x+2x^3 = o(1) \,\, (x\to 0).
- \displaystyle \sum_{n=1}^\infty \frac{x^n}{n} = x+ \frac{x^2}{2} + O(x^3) \,\, (x\to 0).
- \displaystyle \sum_{n=1}^\infty \frac{x^n}{n} = x+ \frac{x^2}{2} + o(x^2) \,\, (x\to 0).
- \displaystyle \sum_{n=1}^\infty \frac{1}{x^n} = \frac{1}{x} + O\left(\frac{1}{x^2}\right)\,\, (x\to\infty).
- \displaystyle \sum_{n=1}^\infty \frac{1}{x^n} = \frac{1}{x} + o\left(\frac{1}{x}\right)\,\, (x\to\infty).
- f(x) , g(x)\xrightarrow{x\to a} 0 のとき, f(x) g(x) = o(f(x)) \,\, (x\to a) .
f(x) \to 0 となる方は,テイラー展開・マクローリン展開によく使われます。例えば, e^x のマクローリン展開を3次まで書くと
e^x = 1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + O(x^4), \quad (x\to 0)
となります。
アルゴリズムの計算時間におけるオーダーとランダウの記号
f(n) \to \infty \,(n\to\infty) となる場合は,コンピューターの計算時間を測るのによく使われます。コンピューターは大量の処理をこなすため,計算時間は非常に重要です。
たとえば, n 個のものを並び替える「ソート (sort)」については様々なアルゴリズムが知られており,代表的なもののみを挙げると,平均計算時間は以下の表になっています。
| ソートアルゴリズム | 平均計算時間 |
|---|---|
| バブルソート | O(n^2) |
| 選択ソート | O(n^2) |
| クイックソート | O(n \log n) |
| マージソート | O(n \log n) |
n^2 と n\log n は n が大きいとき,何千倍・何万倍もの差がつきます。これは,計算時間が何千倍・何万倍にもなることを意味しており,実務の上で考慮せねばならない非常に大事な要素です。