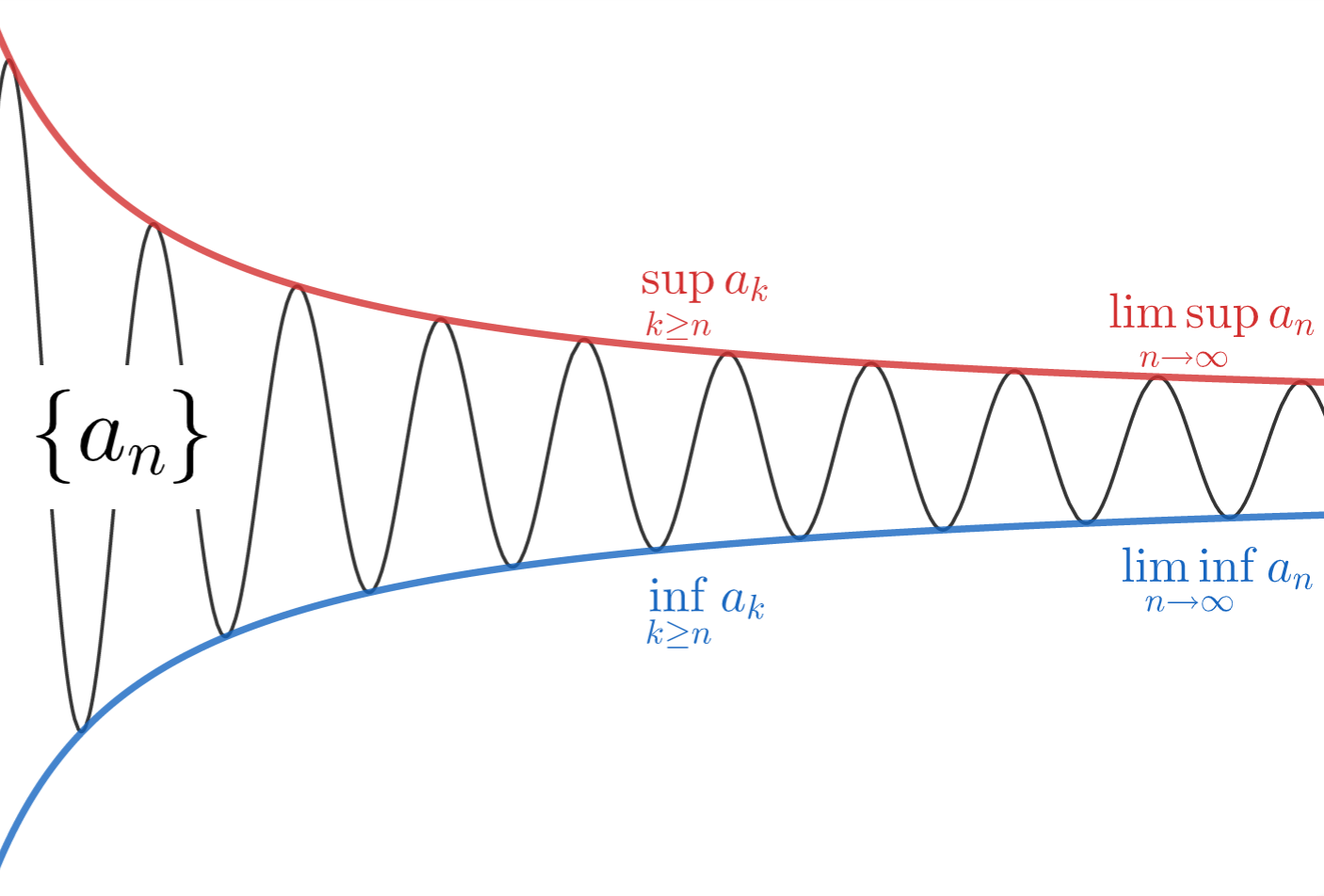
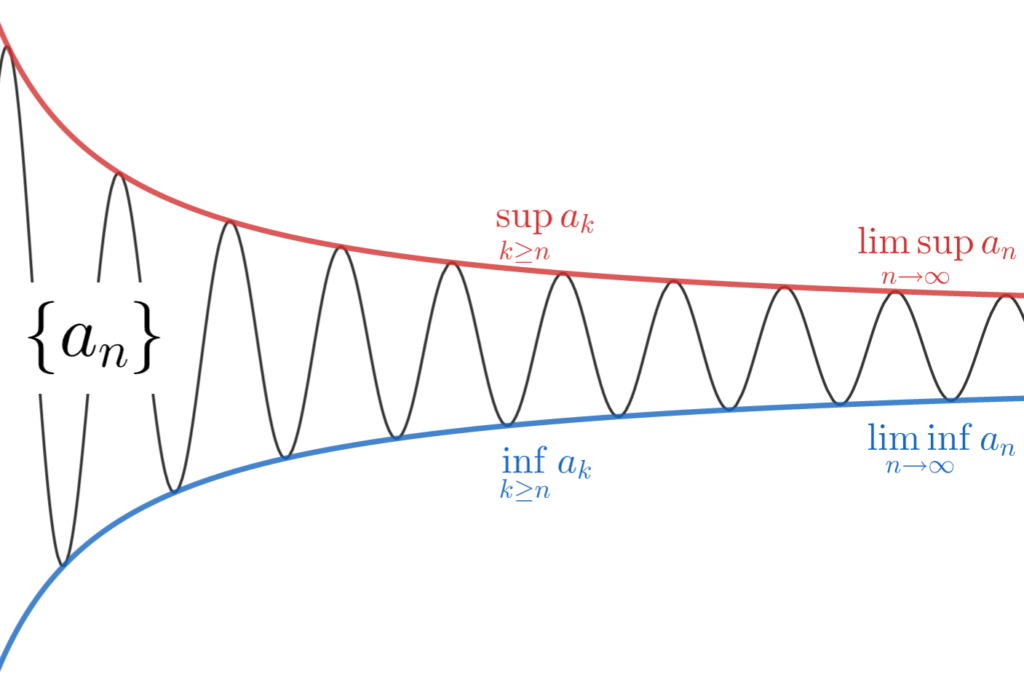
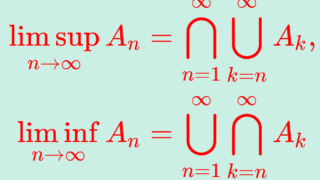上極限・下極限の定義をし,その具体例と重要な性質2つを確認・証明していきましょう。
数列における上極限,下極限(limsup,liminf)の定義
定義(上極限・下極限;数列版)
\{a_n\} を実数列とする。このとき,
\color{red} \limsup_{n\to\infty} a_n = \lim_{n\to\infty}\left( \sup_{k\ge n}a_k\right)
を上極限 (limit superior) といい,
を下極限 (limit inferior) という。
\limsup_{n\to\infty} a_n , \liminf_{n\to\infty} a_n はそれぞれ \varlimsup_{n\to\infty} a_n, \varliminf_{n\to\infty} a_n とかくこともある。
ここで,数列 \left\{ \sup_{k\ge n}a_k\right\}_n , \left\{ \inf_{k \ge n} a_k \right\}_n はそれぞれ単調減少・単調増加ですから,上極限・下極限は \pm\infty も含めると必ず存在することに注意しましょう(→上に有界な単調増加数列は収束することの証明)。極限とは違う性質ですね。
また, \sup_{k\ge n}a_n \ge \inf_{k \ge n} a_n であることと,極限の大小関係が一致することから,
\limsup_{n\to\infty} a_n \ge \liminf_{n\to\infty} a_n
も成り立ちます(→極限の性質6つの証明(一意性,和,積,商,大小関係))。
上極限,下極限(limsup,liminf)の具体例
具体例を挙げましょう。
例1.
\color{red} a_n = (-1)^n と定めると,
\limsup_{n\to\infty} a_n = 1, \quad \liminf_{n\to\infty} a_n = -1
である。
実際, \displaystyle \sup_{k\ge n} a_k= 1, \, \inf_{k\ge n} a_k = -1 なので明らかですね。
例2.
\color{red} a_n = (-1)^n /n と定めると,
\limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n = 0
である。
実際,
\begin{aligned} \sup_{k\ge n} a_k&= \frac{1}{2[n/2]} \xrightarrow{n\to\infty} 0, \\ \inf_{k\ge n} a_k &=- \frac{1}{2[(n+1)/2]-1}\xrightarrow{n\to\infty} 0 \end{aligned}
(ただし[\cdot] は床関数(ガウス記号))なので,成立します。
例3.
\color{red} a_n = n と定めると,
\limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n = \infty
である。
実際,
\begin{aligned} \sup_{k\ge n} a_k= \infty, \quad \inf_{k\ge n} a_k =n \xrightarrow{n\to\infty} \infty \end{aligned}
のため,成立します。
なんとなくイメージが湧いたでしょうか。図で描くと以下のようなイメージです。
上極限,下極限(limsup,liminf)の性質
上極限・下極限の性質のうち,以下の2つ
- 上極限・下極限に収束する部分列の存在
- 上極限・下極限が一致 ⇒ 極限の存在
を順に確認していきましょう。
上極限,下極限に収束する部分列の存在
定理(上極限・下極限に収束する部分列の存在)
\{a_n\} を実数列とし, \limsup_{n\to\infty} a_n = \alpha, \liminf_{n\to\infty} a_n = \beta と定める。
このとき,ある部分列 \{ a_{\varphi_1(n)}\}, \{a_{\varphi_2(n)}\} が存在して,
\color{red} \lim_{n\to\infty} a_{\varphi_1(n)} = \alpha, \quad \lim_{n\to\infty} a_{\varphi_2(n)} = \beta
とできる。
証明
証明では \limsup の方の \alpha が有限のときのみ示すことにします。その他もほぼ同様だからです。
証明
\varphi_1(1) = 1 と定め \varphi_1(n-1) まで定まったとして, \varphi_1(n) を帰納的に定めよう。
極限の定義により,ある N_n \ge 1 が存在して,
とできる。とくに, {N'}_n = \max\{ N_n, \varphi(n-1) \} と定めると,
\left| \sup_{k \ge {N'}_n} a_k - \alpha \right| < \frac{1}{n} である。
上限(sup)の定義により,ある K_n \ge {N'}_n が存在して,
0 \le \sup_{k \ge {N'}_n} a_k - a_{K_n} \le \frac{1}{n}
とできる。 \varphi_1(n) = K_n と定めよう。すると,
よって \lim_{n\to\infty} a_{\varphi(n)} = \alpha が成立する。
証明終
上極限,下極限が一致 ⇒ 極限の存在
定理(上極限・下極限が一致 ⇒ 極限の存在)
\{a_n\} を実数列とする。
\limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n = \alpha \in [-\infty, \infty]
が成立するとき,
である。
なおこのことから,数列の収束・発散は上極限・下極限を用いることで,以下の3つに分類されます。
- \displaystyle \limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n かつ有限値のとき \displaystyle \lim_{n\to\infty}a_n は収束する
- \displaystyle \limsup_{n\to\infty} a_n = \liminf_{n\to\infty} a_n =\pm\infty のとき \displaystyle\lim_{n\to\infty} a_n は \pm \infty に発散する
- \displaystyle \limsup_{n\to\infty} a_n \ne \liminf_{n\to\infty} a_n のとき \{a_n\} は振動する(発散する)
定理の証明をしましょう。
証明
証明では \alpha が有限値のときのみ扱います。
証明
\varepsilon > 0 とする。このとき,ある N \ge 1 が存在して,
\begin{aligned} n \ge N &\implies \left|\sup_{k\ge n}a_k - \alpha \right| < \varepsilon, \\ n \ge N &\implies \left|\inf_{k\ge n}a_k - \alpha \right| < \varepsilon \end{aligned}
とできる。 \displaystyle \inf_{k\ge n}a_k \le a_n \le \sup_{k\ge n}a_k であることに注意すると, n \ge N ならば
となる。すなわち, \lim_{n\to\infty} a_n = \alpha である。
証明終
なお,はさみうちの原理を認めると,
\inf_{k\ge n} a_k \le a_n \le \sup_{k\ge n} a_k
の各辺 n\to\infty とすることでも証明可能ですね。
上極限集合・下極限集合
集合列に対しても上極限・下極限が定義できます。
定義(上極限集合・下極限集合・極限集合)
集合列 \{A_n\} に対し,
\color{red}\begin{gathered} \limsup_{n\to\infty} A_n =\bigcap_{n=1}^\infty \bigcup_{k=n}^\infty A_k, \\ \liminf_{n\to\infty} A_n = \bigcup_{n=1}^\infty \bigcap_{k=n}^\infty A_k \end{gathered}
をそれぞれ上極限集合 (limit superior set),下極限集合 (limit inferior set) という。
また,この両者が一致するとき,それを \color{red} \lim_{n\to\infty} A_n とかき,これを極限集合 (limit set) という。
集合列の場合であっても,数列と同じような性質が成立します。これについて詳しくは以下の記事で解説しています。