双曲線関数 \sinh, \cosh, \tanh の逆関数 \sinh^{-1}, \cosh^{-1}, \tanh^{-1} について考えましょう。
逆双曲線関数(arcsinh,arccosh,arctanh)
まずは双曲線関数を復習し,それをもとにその逆関数である逆双曲線関数を定義していきましょう。
双曲線関数の復習
双曲線関数は
\begin{aligned}
\sinh x &= \frac{e^{x} - e^{-x} }{2}, \\
\cosh x &= \frac{e^{x} + e^{-x}}{2},\\
\tanh x &= \frac{\sinh x}{\cosh x} = \frac{ e^{x} - e^{-x}}{e^{x} + e^{-x}}
\end{aligned}
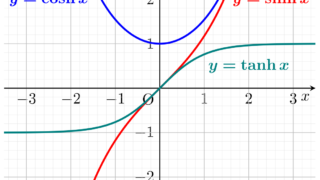
と定義され,そのグラフは以下のようになりました。
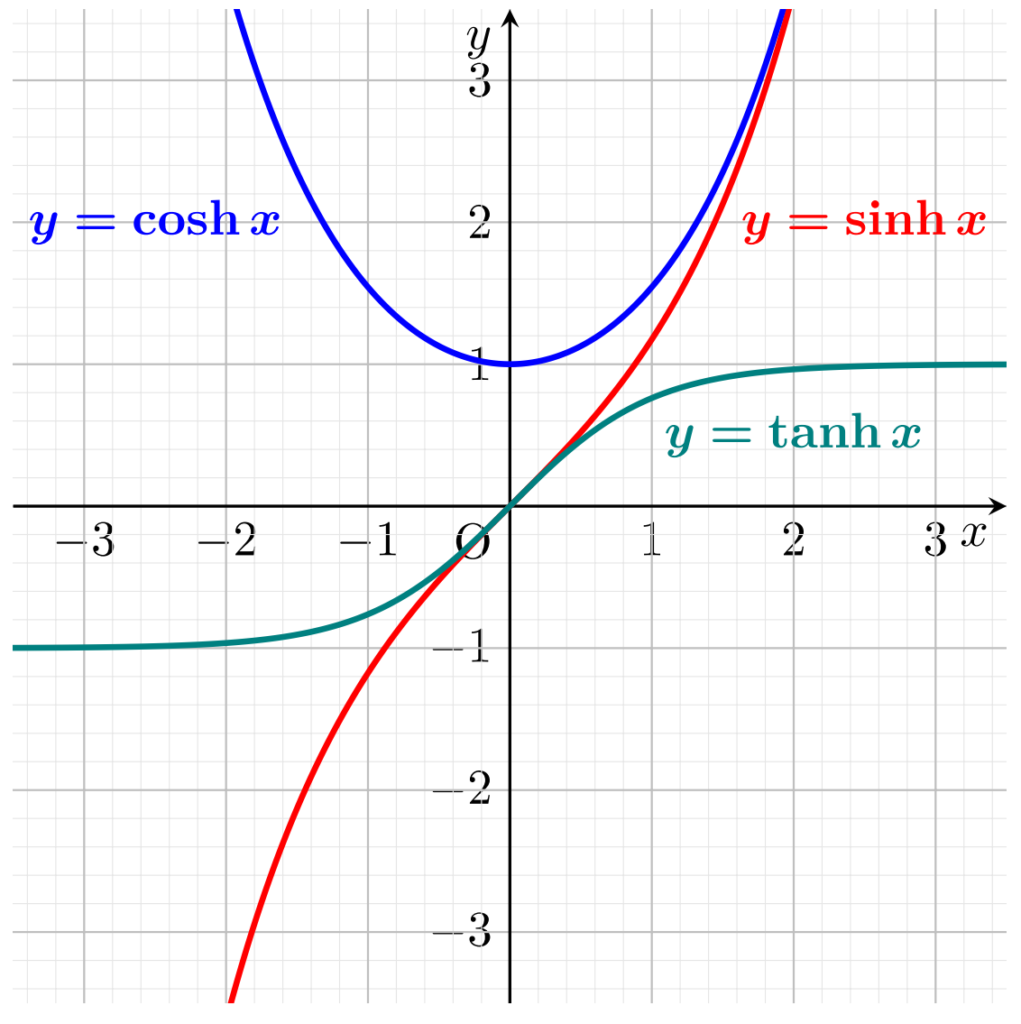
これにより,
\begin{aligned} \sinh &\colon \mathbb{R} \to \mathbb{R} , \\ \cosh &\colon \textcolor{red}{[0, \infty)} \to \textcolor{red}{[1,\infty)}, \\ \tanh &\colon \mathbb{R} \to \textcolor{red}{(-1,1) } \end{aligned}逆双曲線関数の定義
定義(逆双曲線関数)
\begin{aligned} \sinh^{-1} &\colon \mathbb{R} \to \mathbb{R} , \\ \cosh^{-1} &\colon [1, \infty) \to [0,\infty), \\ \tanh^{-1} &\colon \mathbb{(-1,1)} \to \mathbb{R} \end{aligned}
が定義される。これを逆双曲線関数 (inverse hyperbolic function) という。 \color{red} \sinh^{-1} はこれ以外にも, \color{red}\operatorname{arcsinh}, \operatorname{arsinh} などと書かれる。
逆双曲線関数は既存の関数を用いて書くことができます。それが以下の定理です。
逆双曲線関数の既存の関数を用いた表記
定理(逆双曲線関数の表記)
\color{red} \begin{aligned} \sinh^{-1} x &= \log(x+\sqrt{x^2+1}), \quad x \in \mathbb{R}, \\ \cosh^{-1} x &= \log(x+\sqrt{x^2-1}), \quad x\ge 1 , \\ \tanh^{-1} x &= \frac{1}{2} \log \frac{1+x}{1-x}, \quad -1<x<1 \end{aligned}
と書ける。
証明しておきましょう。
証明
\sinh^{-1} x = \log(x+\sqrt{x^2+1}), \,\,x \in \mathbb{R} について
y = \sinh^{-1} x とすると,\displaystyle x = \sinh y = \frac{e^y - e^{-y} }{2} より,
e^{2y} - 2xe^y - 1 = 0
2次方程式の解の公式を用いてこれを解くと,特に e^y > 0 に注意して, e^y = x + \sqrt{x^2 + 1} となる。よって y = \log(x+\sqrt{x^2+1} ) が分かった。
\cosh^{-1} x = \log(x+\sqrt{x^2-1}), \,\, x\ge 1 について
y = \cosh^{-1} x とすると, \displaystyle x = \cosh y = \frac{e^y + e^{-y}}{2} より,
e^{2y} -2xe^y +1 = 0
であるから, y \ge 0 に注意して,同様に2次方程式の解の公式を用いて解くと, y = \log(x+\sqrt{x^2 - 1}) が分かる。
\displaystyle \tanh^{-1} x = \frac{1}{2} \log \frac{1+x}{1-x},\,\, -1<x<1 について
y = \tanh^{-1} x とすると, \displaystyle x = \tanh y = \frac{e^y - e^{-y}}{e^y + e^{-y}} = \frac{e^{2y} - 1}{e^{2y} + 1} である。これを整理すると,
(e^{2y} + 1) x = e^{2y} - 1
となる。よって (1-x)e^{2y} = 1+x なので,\displaystyle y = \frac{1}{2} \log\frac{1+x}{1-x} が分かる。
証明終
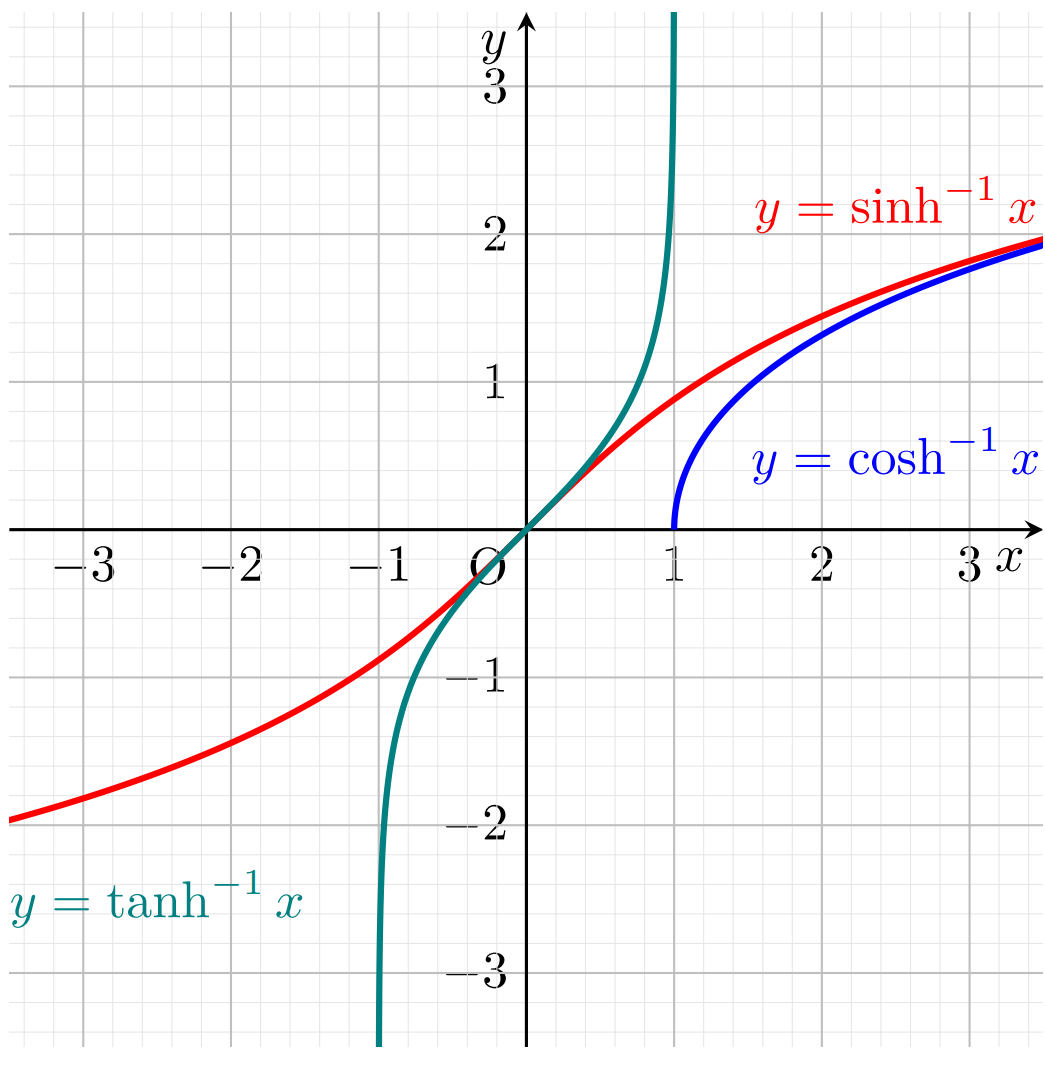
逆双曲線関数のグラフ
それぞれのグラフを描きましょう。
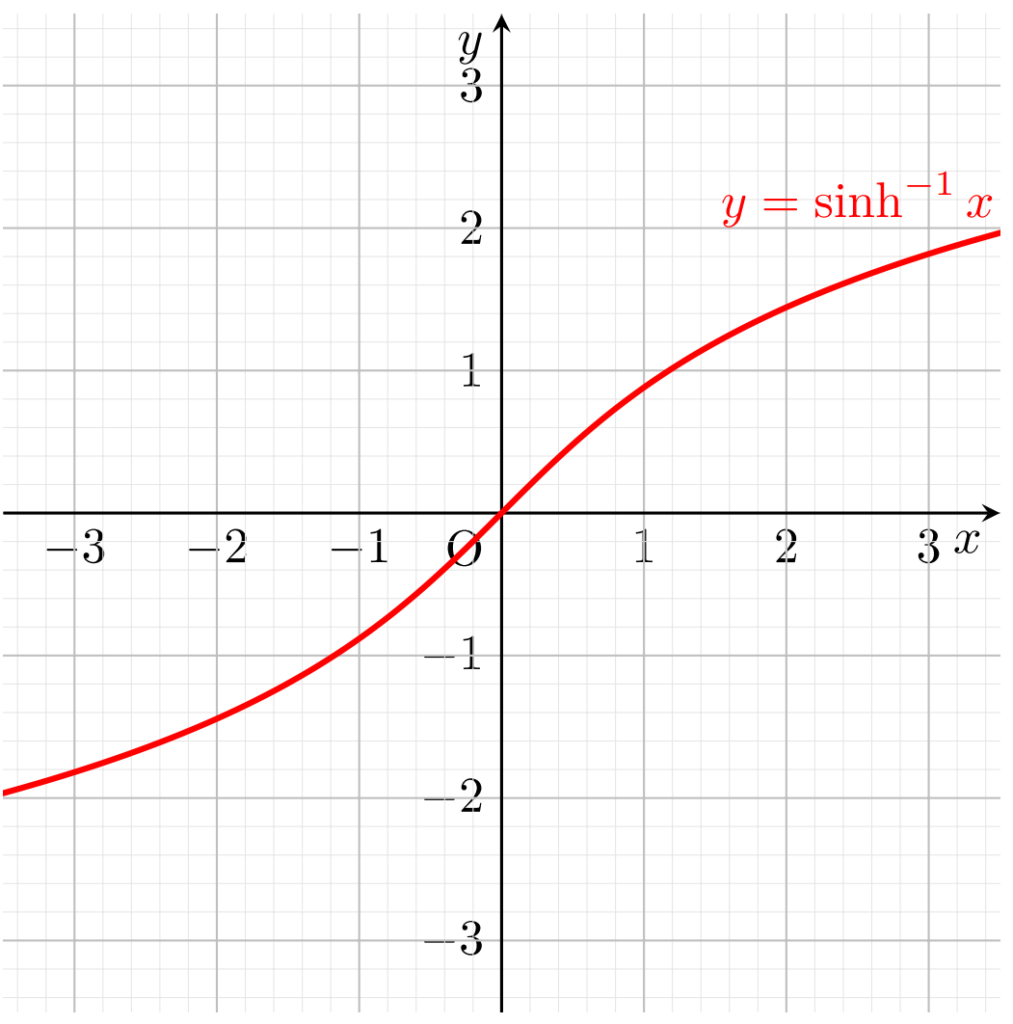
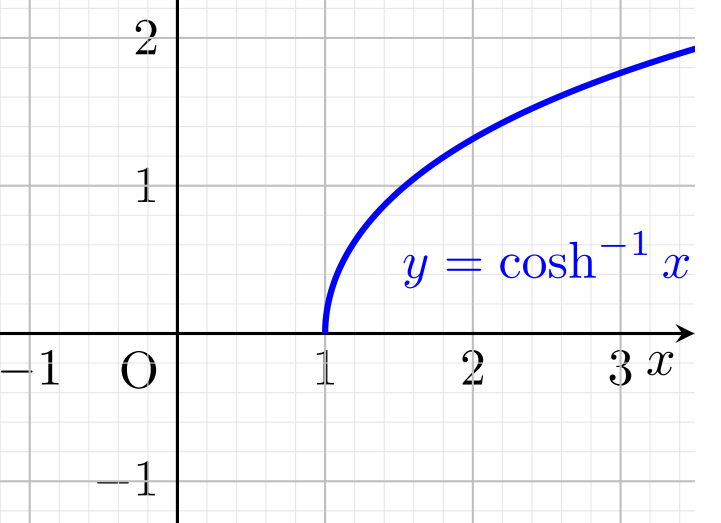
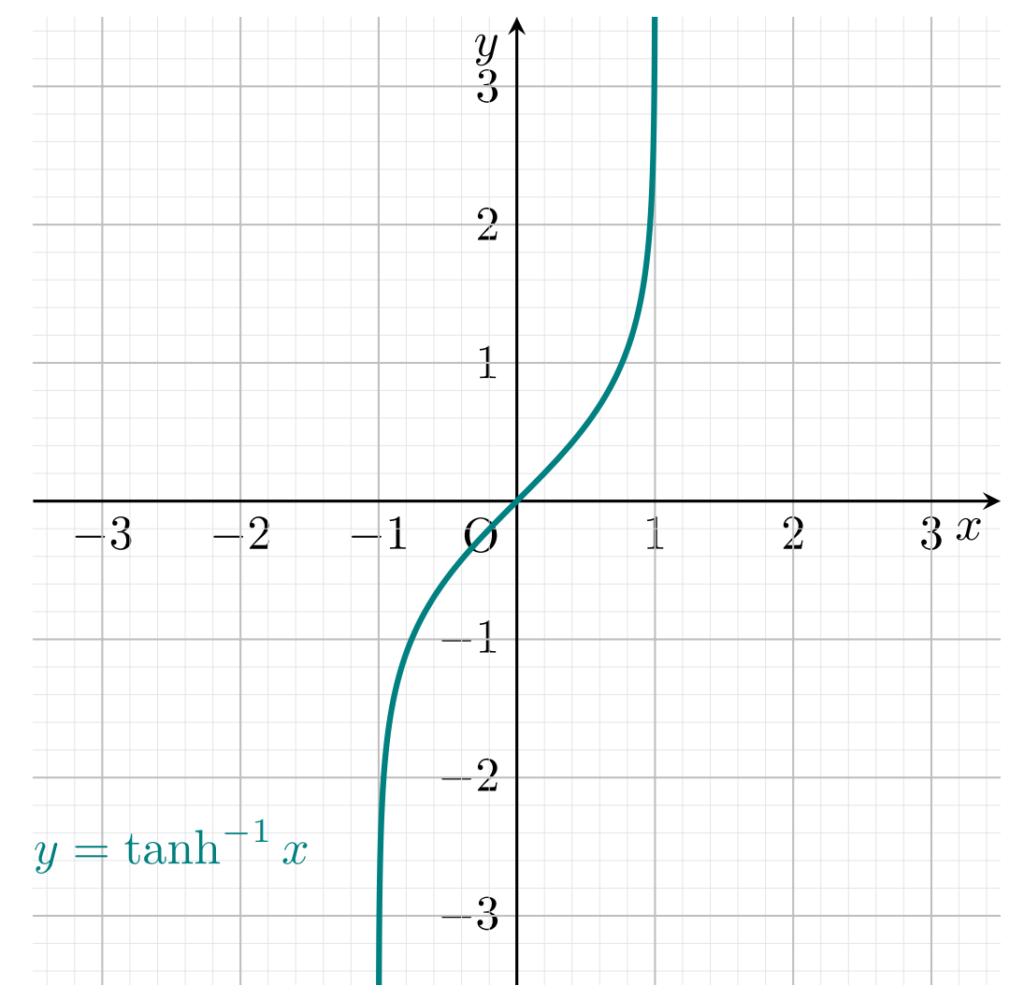
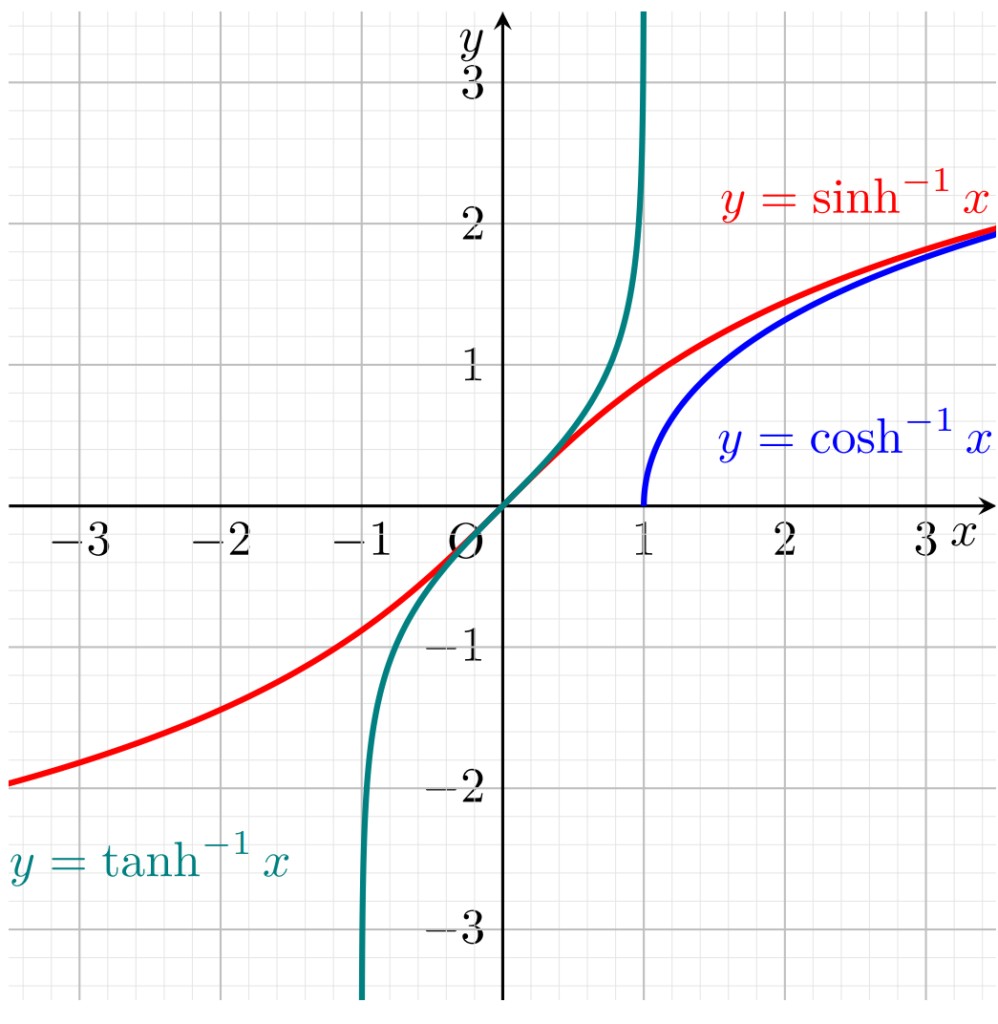
逆双曲線関数の性質
逆双曲線関数の性質を「基本的な性質」「微分」「積分」に分けて挙げていきましょう。
基本的な性質
定理(逆双曲線関数の基本的な性質)
- \sinh^{-1} (-x) = - \sinh^{-1} x. (奇関数)
- \cosh^{-1} (-x) = \cosh^{-1} x . (偶関数)
- \tanh^{-1} (-x) = - \tanh^{-1} x . (奇関数)
逆双曲線関数の微分
定理(逆双曲線関数の微分)
- \displaystyle (\sinh^{-1} x)' = \frac{1}{\sqrt{x^2+1}}.
- \displaystyle (\cosh^{-1} x)' = \frac{1}{\sqrt{x^2-1}}.
- \displaystyle (\tanh^{-1} x)' = \frac{1}{1-x^2}.
この微分を逆に用いると,有名な積分の公式を得ることができます。
a> 0 とする。
- \color{red} \displaystyle \int \frac{1}{\sqrt{x^2 + a^2} } = \sinh^{-1} \frac{x}{a} + C= \log(x+\sqrt{x^2+a^2}) + C'.
- \color{red} \displaystyle \int \frac{1}{\sqrt{x^2-a^2}} = \cosh^{-1} \frac{x}{a} + C = \log(x+\sqrt{x^2-a^2}) + C', \,\, x \ge a.
ただし, C, C' は積分定数。
逆双曲線関数の積分
定理(逆双曲線関数の積分)
- \displaystyle \int \sinh^{-1} x \, dx =x \sinh^{- 1} x- \sqrt{x^2+1} + C.
- \displaystyle \int \cosh^{-1} x \, dx = x \cosh^{-1} x - \sqrt{x^2-1} + C.
- \displaystyle \int \tanh^{-1} x\, dx = x \tanh^{-1} x + \frac{\log(1-x^2)}{2} + C.
ただし, C は積分定数。
もっとほかの積分についてはWikipediaを参照してください。