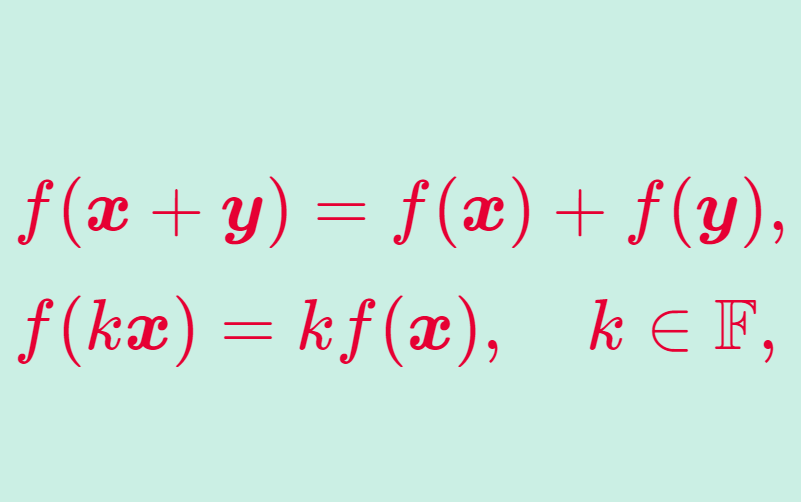線形代数学ではとても大事な写像である,線形写像とは,ラフにいうと
- f(\boldsymbol{x}+ \boldsymbol{y}) = f(\boldsymbol{x}) + f(\boldsymbol{y}),
- f(k\boldsymbol{x}) = kf(\boldsymbol{x})
の両方をみたす写像のことです。これについて,そのちゃんとした定義と,基本的な性質と具体例8つを確認しましょう。
線形写像の定義
線形写像の基本的な定義
定義(線形写像)
V, W を \mathbb{F} 上のベクトル空間とする。 f\colon V \to W が線形写像(線型写像; linear map) であるとは,
- f(\boldsymbol{x}+ \boldsymbol{y}) = f(\boldsymbol{x}) + f(\boldsymbol{y}), \quad \boldsymbol{x},\boldsymbol{y} \in V,
- f(k\boldsymbol{x}) = kf(\boldsymbol{x}), \quad k \in \mathbb{F}, \, \boldsymbol{x} \in V
の両方が成立することである。
ベクトル空間の間の,和と定数倍が保存される写像を線形写像というのですね。
なお,この記事においては,「ベクトル空間」が分からなくてもある程度は読めるようになっています。分からない場合は,「和と定数倍が定義されている集合」と思ってください。
線形写像の同値な定義
上と同値な定義を紹介しましょう。以下の定理を見てください。
定理(線形写像の同値な定義)
V, W を \mathbb{F} 上のベクトル空間とする。
このとき, f\colon V \to W が線形写像であること,すなわち,
- f(\boldsymbol{x}+ \boldsymbol{y}) = f(\boldsymbol{x}) + f(\boldsymbol{y}), \quad \boldsymbol{x},\boldsymbol{y} \in V,
- f(k\boldsymbol{x}) = kf(\boldsymbol{x}), \quad k \in \mathbb{F}, \, \boldsymbol{x} \in V
が成立することと,
- f(k\boldsymbol{x} + l \boldsymbol{y}) = k f(\boldsymbol{x}) + l f(\boldsymbol{y} ), \,\, k,l \in \mathbb{F}, \, \boldsymbol{x},\boldsymbol{y} \in V
が成立することは同値である。
この定理のため,線形写像であることを,「 f(k\boldsymbol{x} + l \boldsymbol{y}) = k f(\boldsymbol{x}) + l f(\boldsymbol{y} ), \,\, k,l \in \mathbb{F}, \, \boldsymbol{x},\boldsymbol{y} \in V が成り立つこと」として定義することがあります。これは,元の定義と同値になっているわけです。
同値であることの証明
- f(\boldsymbol{x}+ \boldsymbol{y}) = f(\boldsymbol{x}) + f(\boldsymbol{y}), \quad \boldsymbol{x},\boldsymbol{y} \in V,
- f(k\boldsymbol{x}) = kf(\boldsymbol{x}), \quad k \in \mathbb{F}, \, \boldsymbol{x} \in V
- f(k\boldsymbol{x} + l \boldsymbol{y}) = k f(\boldsymbol{x}) + l f(\boldsymbol{y} ), \,\, k,l \in \mathbb{F}, \, \boldsymbol{x},\boldsymbol{y} \in V
であることを証明しておきましょう。
証明
( \implies について)
和について, f(k\boldsymbol{x} + l \boldsymbol{y}) = f(k\boldsymbol{x}) + f(l \boldsymbol{y}) が成立し,かつ定数倍について f(k\boldsymbol{x}) = kf(\boldsymbol{x}), f(l \boldsymbol{y}) = l f(\boldsymbol{y}) であることから従う。
( \impliedby について)
f(k\boldsymbol{x} + l \boldsymbol{y}) = k f(\boldsymbol{x}) + l f(\boldsymbol{y} ) で k = l = 1 とおくと f(\boldsymbol{x}+ \boldsymbol{y}) = f(\boldsymbol{x}) + f(\boldsymbol{y}) が従い, l = 0 とおくと f(k\boldsymbol{x}) = kf(\boldsymbol{x}) が従う。
証明終
線形写像の具体例8つ
線形写像の性質を述べる前に,先に具体例を挙げていきましょう。
例1.
a \in \mathbb{R} とする。 \color{red} f\colon \mathbb{R} \to \mathbb{R} を \color{red} f(x) = ax とすると,これは線形写像である。
\mathbb{R} を \mathbb{R} 上ベクトル空間と考えています。
線形写像であることは, x, y, k \in \mathbb{R} に対し,
\begin{gathered} f(x) + f(y) = ax + ay = a(x+y) = f(x+y), \\ f(kx) = a(kx) = k(ax) = kf(x) \end{gathered}
であることからわかります。線形写像とは, f(x) = ax のような,「1次の変換」の一般化と思えます。次の例を見てください。
例2.
f\colon \mathbb{R} \to \mathbb{R} を f(x) = x^2 とすると,これは線形写像ではない。
実際, f(1+1) = 4 \ne 2 = f(1) + f(1) なので,線形写像の性質が成立していません。
f(x) = x^2 は「2次の変換」と言えます。線形写像はあくまで「1次の変換」であり,「2次の変換」ではありません。
例3.
f\colon \mathbb{R} \to \mathbb{R} を f(x) = x + 1 とすると,これは線形写像ではない。
線形写像ならば f(0) = 0 でしたから,これは線形写像ではありません。定数項があってはダメです。
例4.
\color{red} f\colon \mathbb{R^3} \to \mathbb{R} を \color{red} f(x,y,z) = x + y + z と定めると,これは線形写像である。
これは「1次の変換」といえますね。
例5.
f\colon \mathbb{R^3} \to \mathbb{R} を f(x,y,z) = |x| + |y| + |z| と定めると,これは線形写像ではない。
実際, f(1,0,0) + f(-1,0,0) = 2 \ne 0 = f(0,0,0) なので,線形写像ではありません。
例6.
\displaystyle \color{red} \frac{d}{dx}\colon C^1(\mathbb{R}) \to C(\mathbb{R}) を,\color{red} f \mapsto f^\prime と定めると,これは線形写像である。
ただし, C^1(\mathbb{R}) は C^1 級関数(微分可能かつ微分が連続な関数)全体の集合, C(\mathbb{R}) は連続関数全体の集合を表す(→ C1級,Cn級,C∞級関数の定義と具体例5つ)。
微分を返す写像は,線形写像というわけです。
実際, (kf+lg)^{\prime} = k f^\prime + l g^\prime なので,線形性を満たしています。
C^1(\mathbb{R}), C(\mathbb{R}) がベクトル空間であることはベクトル空間・部分ベクトル空間の定義と具体例10個の例を確認してください。
例7.
\color{red} f\colon C[0, 1] \to \mathbb{R} を, \color{red} f(x) = \int_0^1 x(t) \, dt と定めると,これは線形写像である。
ただし, C[0, 1] = \{ f\colon [0, 1] \to \mathbb{R} \mid f \text{ is continuous} \} である(continuous とは「連続」という意味)。
積分を返す写像は,線形写像というわけです。
実際, \int_0^1 (kx(t) + l y(t)) \, dt = k \int_0^1 x(t) \, dt + l \int_0^1 y(t) \, dt であることからわかります。
例8.
確率変数 X に対し,その期待値を返す関数 \color{red}E \colon X \mapsto E[X] は線形写像である。
期待値を返す写像は,線形写像というわけです。
実際, E[kX+lY] = k E[X] + l E[Y] なので,線形写像です。
実は,「期待値」というのは,数学では「積分」で定義されるため,これが線形であることは,積分が線形であることから直ちに従います。
線形写像の性質
さて,線形写像の性質をいくつか挙げましょう。
線形写像の基本的な性質
定理(線形写像の性質)
V, W をベクトル空間, f\colon V \to W を線形写像とする。このとき,
- f(\boldsymbol{0}) = \boldsymbol{0}.
また,さらに X をベクトル空間, g\colon W \to X を線形写像とすると,
- g\circ f \colon V \to X も線形写像である。
どちらも覚えるべき重要な性質です。
証明
( f(\boldsymbol{0}) = \boldsymbol{0} について)
f(k\boldsymbol{x}) = kf(\boldsymbol{x}) で, k = 0 とすれば従う。
( g\circ f が線形写像であることについて)
f, g は線形写像であるから,
\begin{aligned} &g\circ f(k\boldsymbol{x} + l \boldsymbol{y}) \\ & = g(kf(\boldsymbol{x} )+ l f(\boldsymbol{y}) \\ &= kg(f(\boldsymbol{x})) + lg(f(\boldsymbol{y})) \\ &= k \, g\circ f(\boldsymbol{x}) + l \, g\circ f(\boldsymbol{y}) \end{aligned}よって g \circ f は線形写像である。
証明終
線形写像のその他の性質
もう少し発展的な性質を紹介しておきましょう。
定理(線形写像の性質2)
V, W をベクトル空間, f\colon V \to W を線形写像とする。このとき,
1-2.の証明については,以下で解説しているため,参照してください。
3.の証明については,以下を参照してください。
線形同型写像
線形写像が全単射のとき,逆写像も線形写像になります。これを線形同型 (linear isomorphism) といいます。これについては,以下で解説しています。