まず,線形写像における像 (image)・核 (kernel) の定義を確認・図解します。そしてそれがベクトル空間になることを証明します。
Im, Ker の定義と図解
定義(像; image,核; kernel)
V, W をベクトル空間とし, f\colon V \to W を線形写像とする。このとき,
\color{red} \operatorname{Im} f = f(V) = \{f(\boldsymbol{x}) \in W \mid \boldsymbol{x} \in V \}
を f の像 (image) といい,
を f の核 (kernel) という。
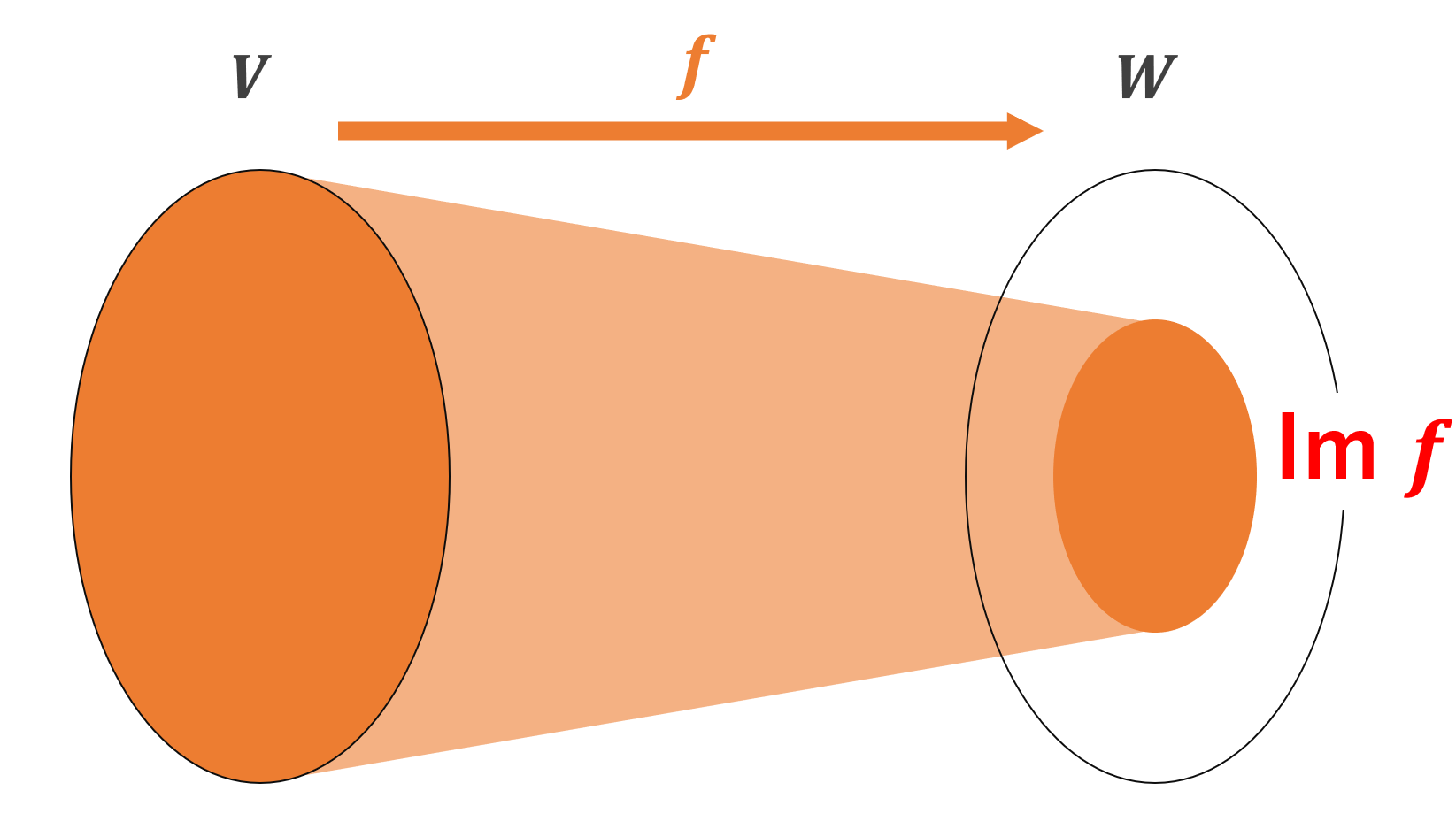
\operatorname{Im} f \subset W, \,\, \operatorname{Ker} f \subset V となることに注意しましょう。
図で描くと,以下のようなイメージです。
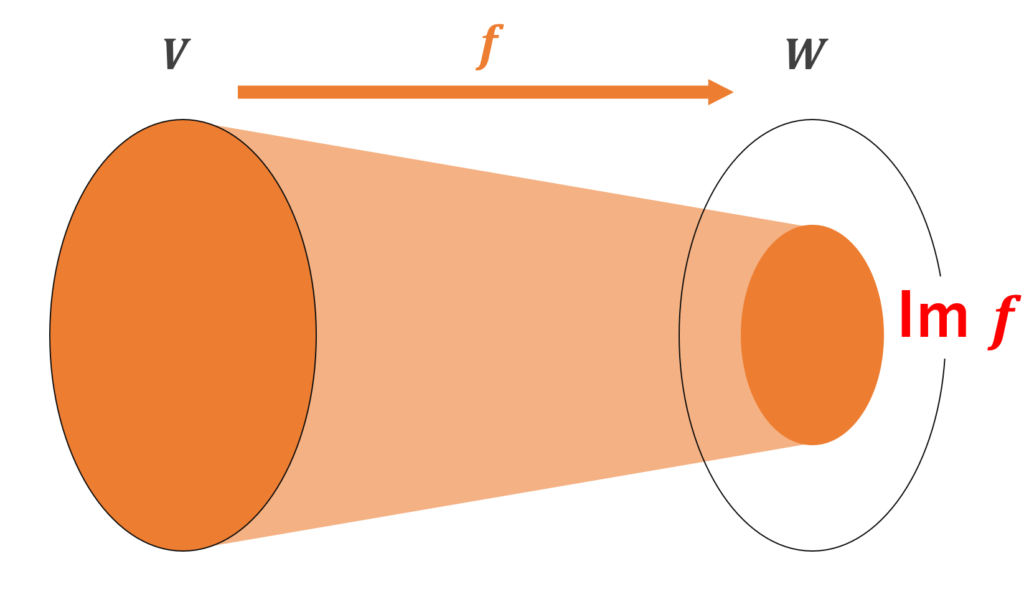
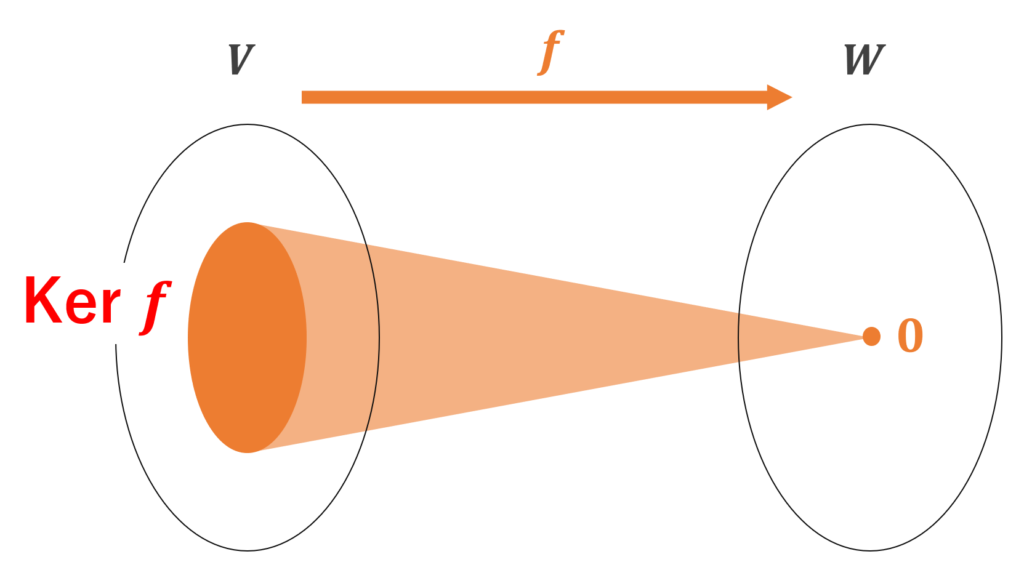
Im, Ker はベクトル空間になる
さて,見出しの通り以下が成立します。
定理の主張
定理
V, W をベクトル空間とし, f\colon V \to W を線形写像とする。このとき,
\operatorname{Im} f ,\,\, \operatorname{Ker} f はそれぞれ W, V の部分ベクトル空間になる。
これを証明しましょう。
証明
証明
示すべきことは,スカラー倍 k_1, k_2 に対し,
\begin{gathered} \boldsymbol{y_1}, \boldsymbol{y_2} \in \operatorname{Im} f \implies k_1 \boldsymbol{y_1} + k_2 \boldsymbol{y_2} \in \operatorname{Im} f, \\ \boldsymbol{x_1}, \boldsymbol{x_2} \in \operatorname{Ker} f \implies k_1 \boldsymbol{x_1} + k_2 \boldsymbol{x_2} \in \operatorname{Ker} f \end{gathered}
となることである(→ ベクトル空間・部分ベクトル空間の定義と具体例10個)。
まず全射について証明しよう。
\boldsymbol{y_1}, \boldsymbol{y_2} \in \operatorname{Im} f とする。定義より,ある \boldsymbol{v_1}, \boldsymbol{v_2} \in V が存在して,
f(\boldsymbol{v_1}) = \boldsymbol{y_1}, f(\boldsymbol{v_2}) = \boldsymbol{y_2}
が成立する。 V はベクトル空間であるから, k_1 \boldsymbol{v_1} + k_2 \boldsymbol{v_2} \in V であり,写像の線形性より
となり,特に k_1 \boldsymbol{y_1} + k_2 \boldsymbol{v_2} \in \operatorname{Im} f である。
後者について証明しよう。
\boldsymbol{x_1}, \boldsymbol{x_2} \in \operatorname{Ker} f とする。定義から, f(\boldsymbol{x_1}) = f(\boldsymbol{x_2}) = \boldsymbol{0} である。線形性から
\begin{aligned} f(k_1\boldsymbol{x_1}+k_2\boldsymbol{x_2}) &= k_1 f(\boldsymbol{x_1}) + k_2f(\boldsymbol{x_2}) \\ &= \boldsymbol{0} \end{aligned}
なので, k_1\boldsymbol{x_1}+k_2\boldsymbol{x_2} \in \operatorname{Ker} f である。
証明終
線形写像とそのIm, Kerにまつわるその他の性質
線形写像と \operatorname{Im}, \operatorname{Ker} に関連するその他の性質を挙げましょう。
線形写像が単射になる必要十分条件
線形写像が単射であるか確認するときは,単に \operatorname{Ker} を見るだけでよいです。
定理(線形写像の単射性)
V, W をベクトル空間, f\colon V\to W を線形写像とする。
このとき,これが単射になる必要十分条件は
となることである。
これについては,以下で解説しています。
線形写像の次元等式
定理(線形写像の次元等式)
V, W をベクトル空間, f\colon V\to W を線形写像とする。このとき,
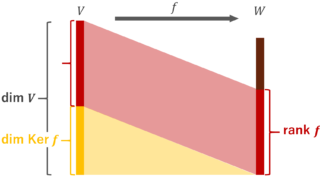
\color{red} \dim V = \operatorname{rank} f + \dim \operatorname{Ker} f
となる。
ここで \operatorname{rank} とは,日本語では階数と呼ばれ, \color{red} \operatorname{rank} f = \dim \operatorname{Im} f と定義されます。
これについては以下で解説しています。