線形写像における次元の等式 \dim V = \operatorname{rank} f + \dim \operatorname{Ker} f を証明し，そのことから従う定理として，線形写像の全射・単射性と \operatorname{rank} との関係を述べましょう。
線形写像の次元定理 dim V = rank f + dim ker f
定理（線形写像の次元定理）
V, W をベクトル空間， f\colon V\to W を線形写像とする。このとき，
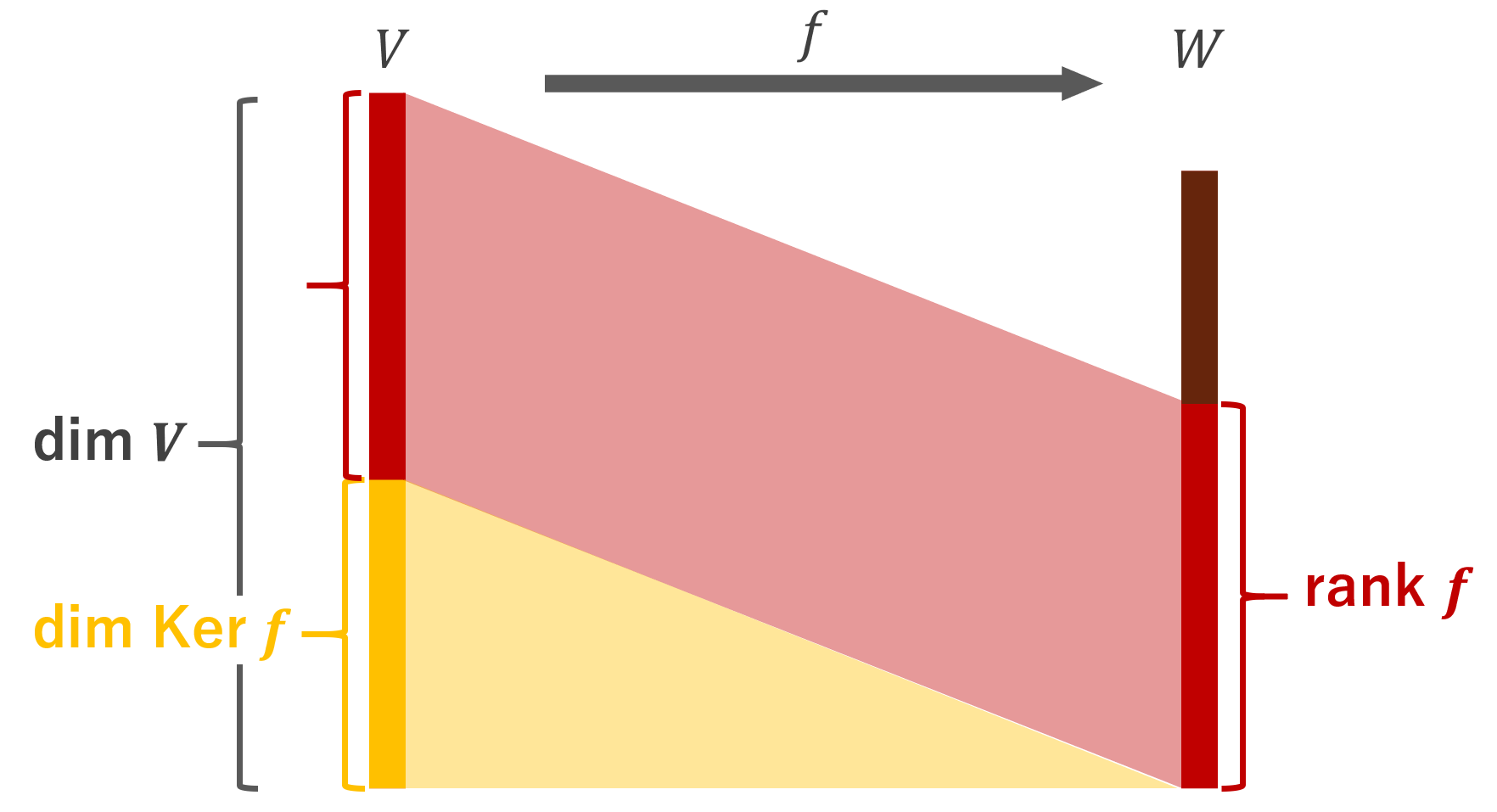
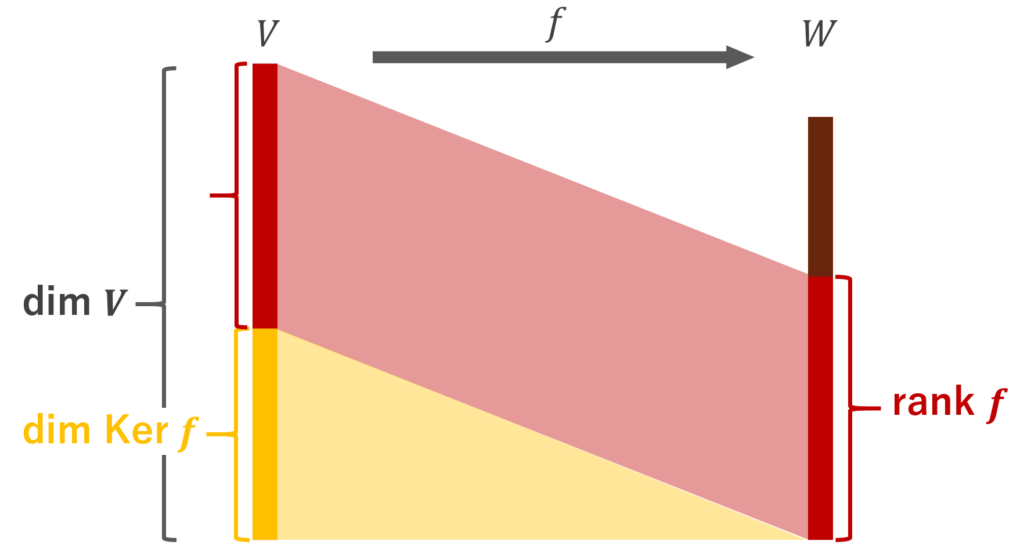
\color{red} \dim V = \operatorname{rank} f + \dim \operatorname{Ker} f
となる。
ここで \operatorname{rank} とは，日本語では階数と呼ばれ， \color{red} \operatorname{rank} f = \dim \operatorname{Im} f と定義されます。
定義中の \dim すなわち，ベクトル空間の次元については以下で解説しています。
定義中の \operatorname{Im}, \operatorname{Ker} すなわち，線形写像における像・核に関しては，以下で解説しています。
図で描くと，以下のようなイメージです。
早速証明しましょう。
次元定理の証明
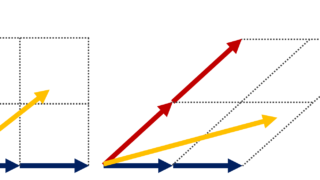
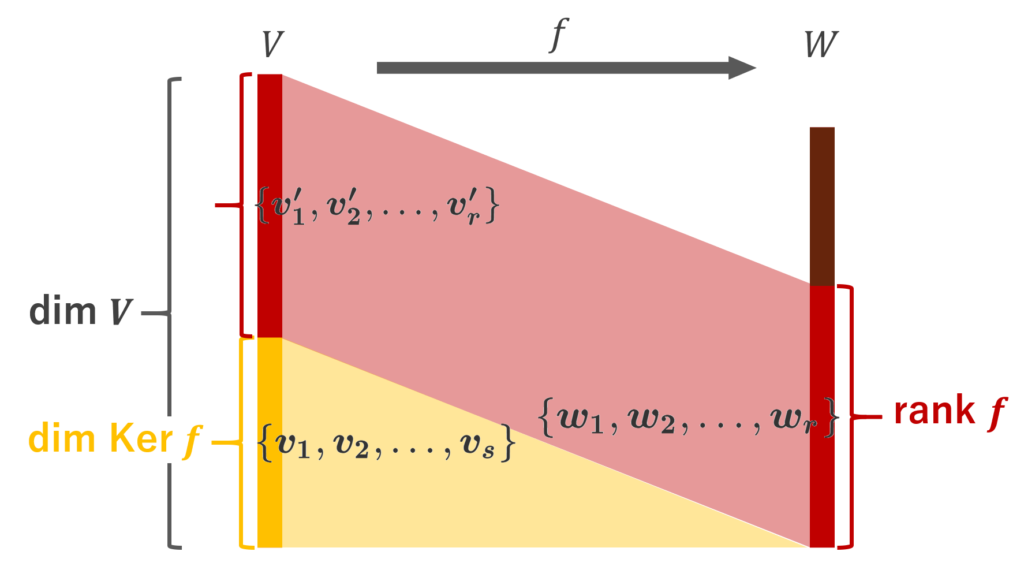
証明の概略は図のような感じです。カッコ内は基底を表します。
証明
\operatorname{Im} f, \operatorname{Ker}f はベクトル空間であったことに注意(→ 線形写像の像(Im),核(Ker)の定義とそれが部分空間になる証明)。
r = \dim \operatorname{Im} f, \, s = \dim \operatorname{Ker} f とし， \operatorname{Im} f, \, \operatorname{Ker} f の基底をそれぞれ \{ \boldsymbol{w_1}, \boldsymbol{w_2}, \dots , \boldsymbol{w_r} \} ,\, \{ \boldsymbol{v_1}, \boldsymbol{v_2}, \dots , \boldsymbol{v_s} \}とする。
1 \le i \le r に対し， \boldsymbol{w_i} \in \operatorname{Im} f より，ある \boldsymbol{v^\prime_i} \in V が存在して， f(\boldsymbol{v^\prime_i}) = \boldsymbol{w_i} とできる。
\{ \boldsymbol{v^\prime_1}, \boldsymbol{v^\prime_2}, \dots , \boldsymbol{v^\prime_r} , \boldsymbol{v_1}, \boldsymbol{v_2}, \dots , \boldsymbol{v_s} \} が V の基底になっていることを示せば， \dim V = \operatorname{rank} f + \dim \operatorname{Ker} f は， r+s = r + s となって証明が終わる。よってこれを示そう。
V の基底になっていることを示すには，
- それらが一次独立であること
- 任意の \boldsymbol{v} \in V がそれらの一次結合でかけること
を示せばよい。順番に示していこう。
一次独立であること
k^\prime_1 \boldsymbol{v^\prime_1} + \cdots + k^\prime_r \boldsymbol{v^\prime_r} + k_1 \boldsymbol{v_1} + \cdots + k_s \boldsymbol{v_s} = \boldsymbol{0}
とおく。両辺を f でうつすと，
となり， \{ \boldsymbol{w_1}, \boldsymbol{w_2}, \dots , \boldsymbol{w_r} \} は \operatorname{Im} f の基底なので， k^\prime_1 = \cdots = k^\prime_r = 0 となる。このとき，元の式は
となるが，これは \operatorname{Ker} f の基底の一次結合なので， k_1 = \cdots = k_s = 0 もわかる。
よって k^\prime_1 = \cdots = k^\prime_r = k_1 = \cdots = k_s = 0 なので，一次独立である。
任意の \boldsymbol{v} \in V がそれらの一次結合でかけること
f(\boldsymbol{v}) \in \operatorname{Im} f より，
f(\boldsymbol{v}) = l'_1 \boldsymbol{w_1} + \cdots + l'_r \boldsymbol{w_r}
と書ける。 f(\boldsymbol{v^\prime_i}) = \boldsymbol{w_i} なので，
となり，特に \boldsymbol{v} - l^\prime_1\boldsymbol{v^\prime_1} - \cdots -l^\prime_r\boldsymbol{v^\prime_r} \in \operatorname{Ker} f なので，これは \operatorname{Ker} f の基底の一次結合で書けて，
よって， \boldsymbol{v} は \{ \boldsymbol{v^\prime_1}, \boldsymbol{v^\prime_2}, \dots , \boldsymbol{v^\prime_r}, \boldsymbol{v_1}, \boldsymbol{v_2}, \dots , \boldsymbol{v_s} \} の一次結合で書けている。
証明終
関連する話題
等式 \dim V = \operatorname{rank} f + \dim \operatorname{Ker} f であることと，以下の記事を用いれば，直ちに次の定理が従います。
定理（線形写像の全射・単射性とランク）
\dim V = \operatorname{rank} f + \dim \operatorname{Ker} f は 2.の証明に用います。
他に，関連する話題として，以下の記事を添付しておきましょう。
