ベクトル空間における,「基底」とは,ベクトル空間の元を一次結合で表すためのものであり,「次元」は,その基底の個数を指します。これについての定義を述べ,具体例を挙げましょう。
ベクトル空間の基底と次元
まずは,抽象的で少々分かりにくいですが,先に大事な定義を述べることにしましょう。
以下では, K 上のベクトル空間 V として,一般的な定義を述べます。難しければ, V はベクトルを集めた集合で, K は実数 \mathbb{R} と思っても全く差し支えないです。
ベクトル空間の基底
定義(ベクトル空間の基底)
V を K 上ベクトル空間, 1 \le n \le \infty とする(すなわち無限も許す)。
\boldsymbol{v_1}, \boldsymbol{v_2}, \ldots, \boldsymbol{v_n} \in V に対し,
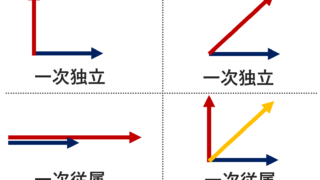
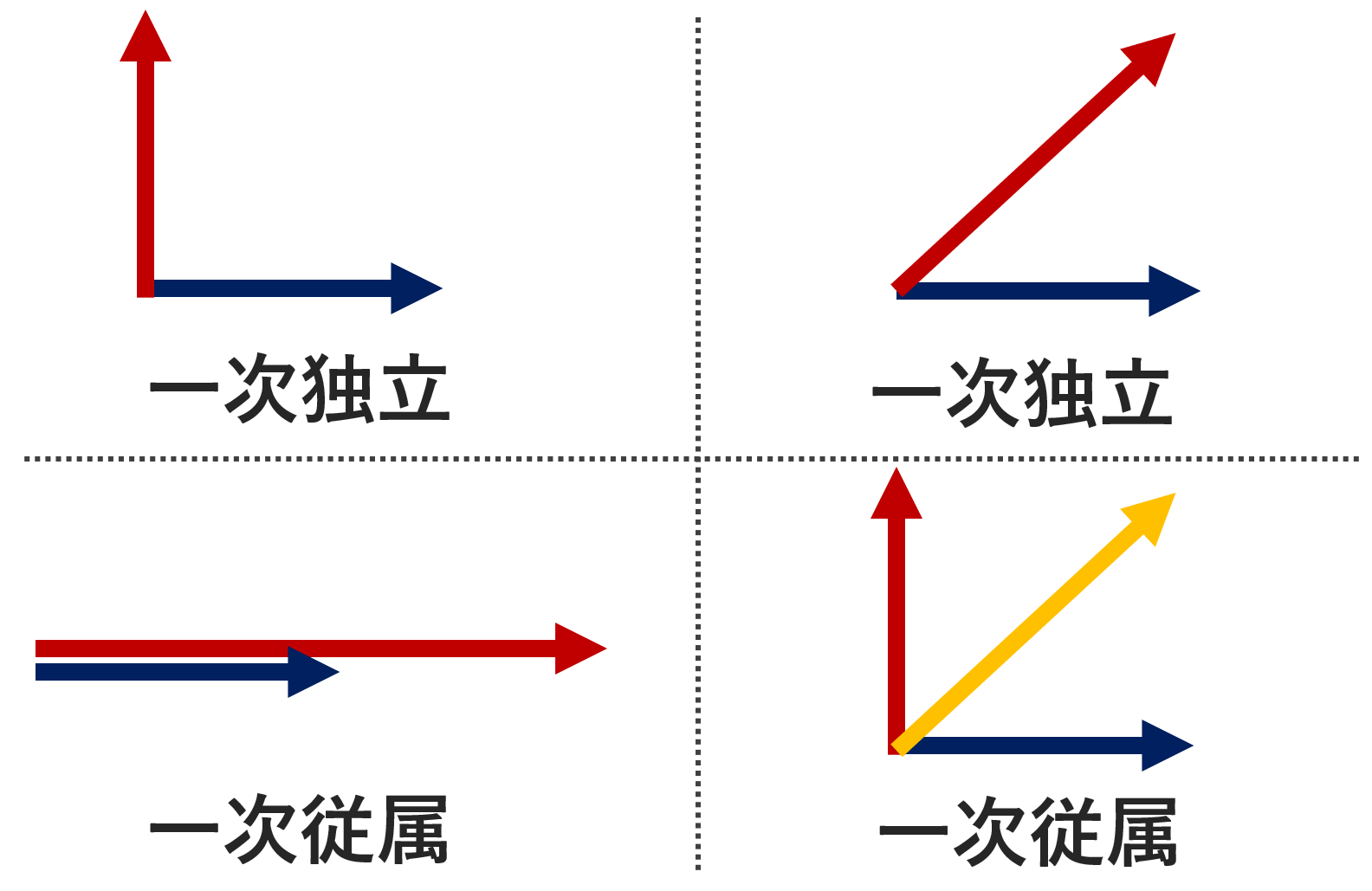
- その任意の有限個が一次独立であり,かつ
- 任意の \boldsymbol{v} \in V に対して,ある有限個の \boldsymbol{v_{i_1}}, \boldsymbol{v_{i_2}}, \ldots ,\boldsymbol{v_{i_l}} \in V と k_{i_1}, k_{i_2},\dots, k_{i_l}\in K が存在して,
\color{red} \boldsymbol{v} = k_{i_1}\boldsymbol{v_{i_1}}+ k_{i_2}\boldsymbol{v_{i_2}} + \cdots + k_{i_l}\boldsymbol{v_{i_l}} とかける
とき, \boldsymbol{v_1}, \boldsymbol{v_2}, \ldots ,\boldsymbol{v_n} を V の基底 (basis) という。
ここで,一次独立について分からない場合は,以下の記事を参照してください。
「一次独立」+「 V の任意の元を表現できる」の2つをみたすものが,基底なわけですね。注意ですが,基底の取り方は一通りとは限りません。
また,最終行「解析学の文脈で~」の部分は,基本的に無視してください。
このとき,以下の定理が成立します。
定理(基底の個数)
基底の個数は,基底の取り方によらず一定である。
これの証明は,一番最後に付録として,行いましょう。
ベクトル空間の次元
基底の個数 n は,基底の取り方によらなかったわけですから, V における不変量として, n に名前を付けることが可能です。
定義(ベクトル空間の次元)
ベクトル空間 V の基底の個数が 1\le n \le \infty であるとき, V の次元 (dimension) は n であるといい,
\color{red} \dim V = n
とかく。
無限個の基底が取れるときは, \dim V =\infty となります。
ベクトル空間の基底・次元の具体例5つ
さて,ここからは具体例を確認していきましょう。
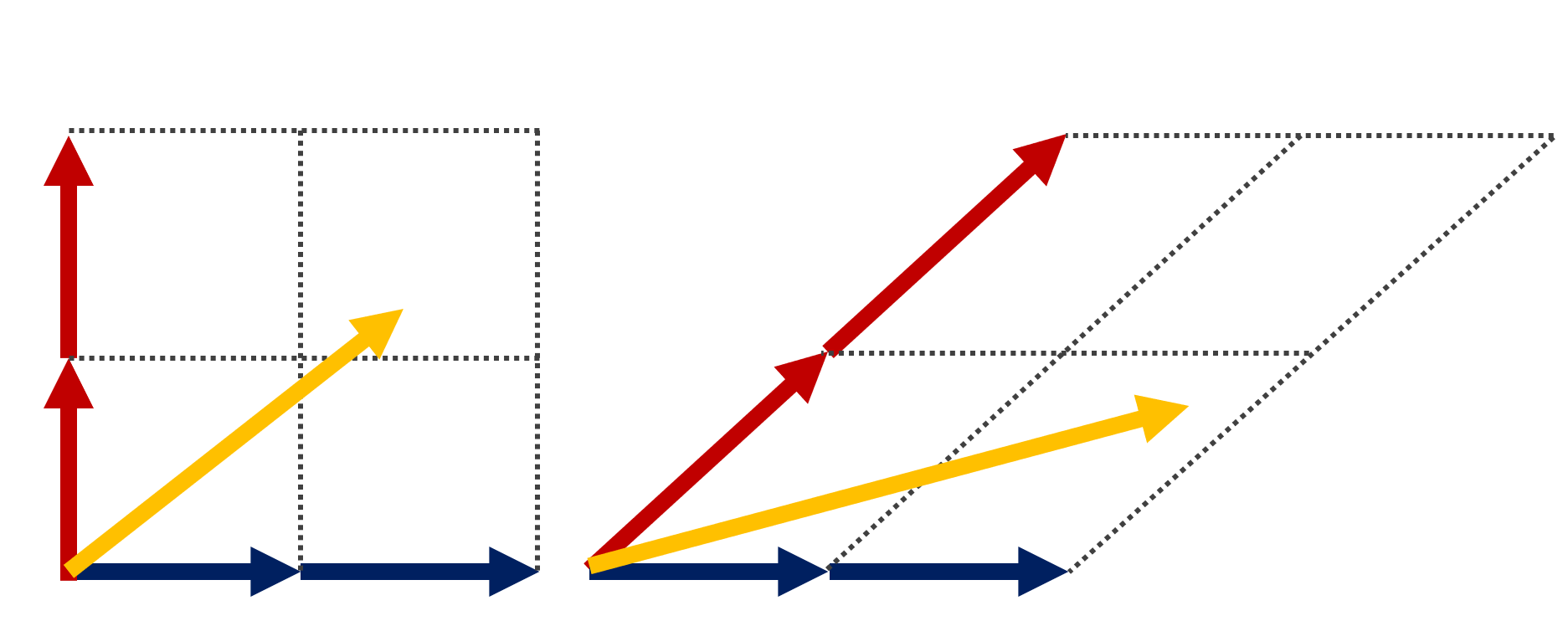
例1 (平面ベクトル)
\textcolor{red}{\mathbb{R}^2 = \{(x, y) \mid x, y \in \mathbb{R}\} } において,
- (1,0), (0, 1) は基底とできる。
- (1,0), (1,1) は基底とできる。
特に,\dim \mathbb{R}^2 = 2 である。
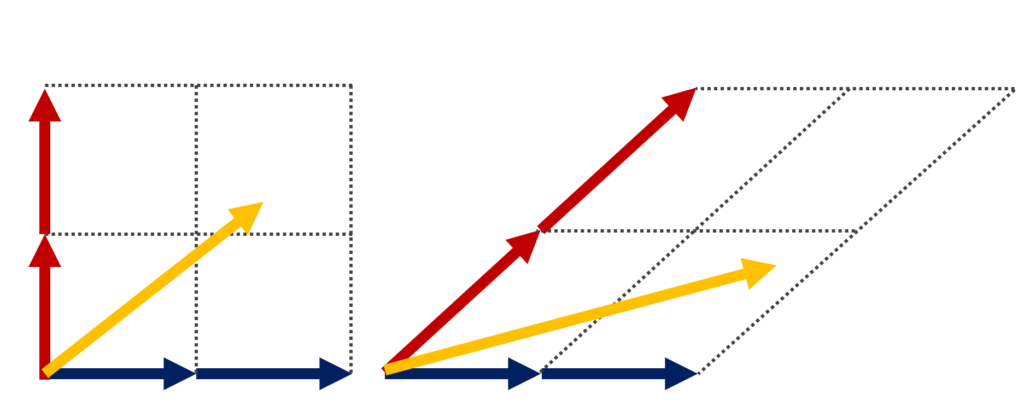
それぞれ,確認していきましょう。確認すべきは,
- 一次独立であること
- それを用いてすべてのベクトルを表せること
の2つでした。
1. k(1,0)+l(0,1) = (0,0) とすると, k=l=0 であるから,一次独立である。また, (x,y)\in\mathbb{R}^2 とすると, (x,y) = x(1,0)+y(0,1) と表せるので,全てのベクトルを表せる。従って,基底である。
2. k(1,0)+l(1,1) = (0,0) とすると, k=l=0 であるから,一次独立である。また, (x,y)\in\mathbb{R}^2 とすると, (x,y) = (x-y)(1,0)+y(1,1) と表せるので,全てのベクトルを表せる。従って,基底である。
基底の個数が 2 ですから, \dim \mathbb{R}^2=2 ですね。
例2.(空間ベクトル)
\textcolor{red}{\mathbb{R}^3 = \{(x, y, z) \mid x, y, z \in \mathbb{R}\} } において,
- (1,0, 0), (0, 1, 0), (0,0,1) は基底とできる。
- (1,0,0), (1,1,0), (0, 2,1) は基底とできる。
特に, \dim \mathbb{R}^3 = 3 である。
それぞれの確認は,演習問題としましょう。
例3.(n次元ベクトル)
\textcolor{red}{\mathbb{R}^n = \{(x_1,x_2, \ldots, x_n) \mid x_1, x_2, \ldots ,x_n \in \mathbb{R}\} } において,
\boldsymbol{e_k} = (0, \ldots, 1, \ldots, 0) , \, 1 \le k \le n (k 番目の要素のみ 1) と定めると, \boldsymbol{e_1}, \boldsymbol{e_2},\ldots, \boldsymbol{e_n} は基底とできる。
特に, \dim \mathbb{R}^n = n である。
例3.は例1,2の一般化ですね。 n 次元ユークリッド空間は,ベクトル空間として n 次元なわけです。(関連:数ベクトルの定義と数ベクトルにおけるノルム・内積)
さて,ここからは具体例のレベルを上げましょう。ベクトル空間について,ある程度理解しているものとします。
例4.(数列)
有限個のみ 0 でない数列全体のなすベクトル空間 \textcolor{red}{l_c= \{ \{a_n\} \mid a_n\in\mathbb{R} , \#\{n\mid a_n \ne 0 \} <\infty \}} において,
\boldsymbol{e_n} = (0, \ldots, 0, 1, 0 , \ldots) , n\ge 1 (n 番目の要素のみ 1) と定めると, \{\boldsymbol{e_n}\}_n は基底とできる。
特に, \dim l_c =\infty である。
有限個のみ 0 でないという制約を設けていますが,これがないと, \{\boldsymbol{e_n}\}_n は基底になりません。これは,ベクトル空間のすべての元が,基底の有限個の一次結合で書けなければならないからで,たとえば (1,1,1,\ldots ) は有限個の一次結合で書けませんね。
ただし,解析学の文脈では,無限和の収束を考えることで, a_n\ne 0 が無限個ある数列についても表せます。よって,全ての数列全体のなすベクトル空間の基底として, \{\boldsymbol{e_n}\}_n を取ることができるようになります。
例5.(多項式)
多項式全体のなすベクトル空間 \textcolor{red}{\mathbb{R}[x] = \{ a_nx^n + \cdots + a_1x+ a_0 \mid a_0, \ldots ,a_n \in \mathbb{R}, n \ge 1 \} } において,
1,x,x^2,\ldots は基底とできる。
特に, \dim \mathbb{R}[x] = \infty である。
【付録】基底の個数は一定であることの証明
さて,最後に以下の定理を証明しておきましょう。
ベクトル空間の基底の個数は,基底の取り方によらない。
次元が well-defined であることを保証する定理です。証明しましょう。
証明
\{\boldsymbol{a_k}\}_{k=1}^m,\; \{\boldsymbol{b_k}\}_{k=1}^n を共に基底とし, m<n としたときに, \{\boldsymbol{b_k}\}_{k=1}^n が一次独立でない(一次従属である)ことを示すことで,基底になり得ないことを言う。特に, n=m+1 としてもよいので,このときに示そう。
m に関する帰納法で示す。 m=1 のとき,\boldsymbol{a_1} はベクトル空間の基底より,
\boldsymbol{b_1} = k_1 \boldsymbol{a_1},\quad \boldsymbol{b_2} = k_2\boldsymbol{a_1}
とかける。特に, (k_1, k_2) \ne (0,0) としてよい(そうでないと \boldsymbol{b_1}, \boldsymbol{b_2} は一次従属である)。このとき,
となって,結局,一次独立でない。
m=s のとき,一次従属が言えるとして, m=s+1 のときを考える。このとき,\{\boldsymbol{a_k}\}_{k=1}^{s+1} は基底であるから,
\begin{aligned}\boldsymbol{b_1} &= k_{11}\boldsymbol{a_1}+\cdots +k_{1\,s+1} \boldsymbol{ a_{s+1}}, \\ &\dots \\ \boldsymbol{b_{s+2}} &= k_{s+2\,1}\boldsymbol{a_1}+\cdots +k_{s+2\,s+1} \boldsymbol{ a_{s+1}} \end{aligned}
とかける。 k_{1\,s+1}=\dots = k_{s+2\, s+1}=0 のとき,m=s の場合に帰着するから,少なくとも一つは 0 でないと思える。このとき, k_{s+2\, s+1}\ne 0 としても一般性を失わない。
1\le j\le s+1 に対して,\boldsymbol{b'_j} = \boldsymbol{b_j} - \dfrac{k_{j\,s+1}}{k_{s+2\, s+1}}\boldsymbol{b_{s+2}} と定めると, \boldsymbol{b'_1}, \dots, \boldsymbol{ b'_{s+1}} は \boldsymbol{ a_1},\dots, \boldsymbol{ a_s} の一次結合でかけている。よって,帰納法の仮定から, \boldsymbol{ b'_1},\dots, \boldsymbol{ b'_{s+1}} は一次従属,すなわち
c_1 \boldsymbol{ b'_1}+\dots+c_{s+1} \boldsymbol{ b'_{s+1}} = \boldsymbol{ 0}
をみたす (c_1,\dots, c_{s+1}) \ne (0,\dots, 0) が存在する。これを \boldsymbol{b_1},\dots, \boldsymbol{ b_{s+2}} の式にかき直すことで,これらが一次従属であることが分かる。
証明終