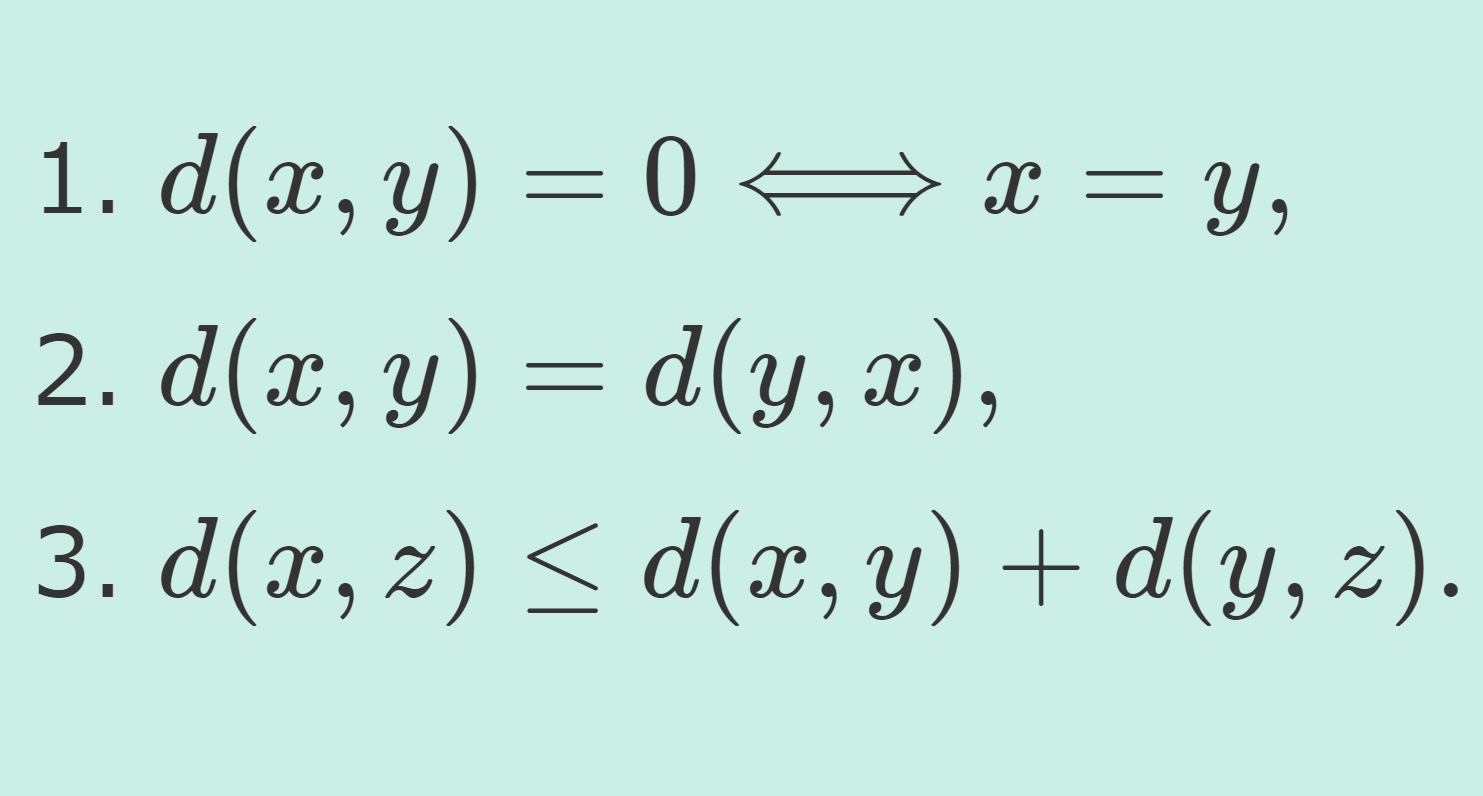距離空間とは,距離の構造にあたる「距離関数」を備えた集合のことです。「距離」は日常的によく使われる言葉ですが,抽象的な数学の上でも考えられるよう,かなり一般化されて定義されます。そんな距離空間について確認し,具体例を確認していきましょう。
距離関数・距離空間の定義
定義(距離関数・距離空間)
X を空でない集合とする。関数 d\colon X \times X \to [0, \infty) が以下の性質をみたすとき,距離関数 (distance function) という。
- d(x, y) = 0 \Longleftrightarrow x = y,
- d(x, y) = d(y, x),
- d(x,z) \le d(x, y) + d(y, z). (三角不等式)
このとき, (X, d) ,または単に X は距離空間 (metric space) であるという。
3つの項目の前に書きましたが, d(x, y) \ge 0 であることにも注意してください。
このように定めると,現実世界における「物と物との距離」の感覚と矛盾しないことが分かります。実際に具体例を確認してみましょう。
距離空間の具体例
例1.(平面におけるユークリッド距離;L^2 距離)
\mathbb{R}^2 = \{ (x_1, x_2) \mid x_1, x_2 \in \mathbb{R} \} は, \boldsymbol{x} = (x_1,x_2), \boldsymbol{y} = (y_1, y_2) に対し,
\textcolor{red}{d(\boldsymbol{x}, \boldsymbol{y}) = \sqrt{(x_1 - y_1)^2 + (x_2-y_2)^2}}
と定めることで,距離空間になる。この距離をユークリッド距離 (Euclidean distance) または L^2 距離という。
高校までにおいて,「平面における2点間の距離」は,三平方の定理を使ってこのように定義したと思います。これは一般的な距離で,ユークリッド距離と呼ばれます。距離の定義をみたすか確認していきましょう。
d(\boldsymbol{x}, \boldsymbol{y}) = 0 \Leftrightarrow \boldsymbol{x} = \boldsymbol{y} と d(\boldsymbol{x}, \boldsymbol{y}) = d(\boldsymbol{y}, \boldsymbol{x}) が成立することはほぼ明らかでしょう。三角不等式については, \boldsymbol{x} = (x_1, x_2), \boldsymbol{y} = (y_1,y_2), \boldsymbol{z} = (z_1, z_2) に対し, a_i = x_i - y_i, b_i = y_i - z_i とおくと,
\begin{aligned} &d(\boldsymbol{x}, \boldsymbol{z})^2\\ &= (a_1+b_1)^2 + (a_2+b_2)^2 \\ &= (a_1^2 + a_2^2) + (b_1^2 + b_2^2) + 2(a_1b_1+a_2b_2) \\ &\le (a_1^2 + a_2^2) + (b_1^2 + b_2^2) + 2\sqrt{(a_1^2+a_2^2)(b_1^2+b_2^2)} \\ &= \left(\sqrt{a_1^2+a_2^2}+\sqrt{b_1^2+b_2^2}\right)^2 \\ &= (d(\boldsymbol{x}, \boldsymbol{y}) + d(\boldsymbol{y},\boldsymbol{z}))^2 \end{aligned}であることからわかります。ただし,不等式の部分は,コーシーシュワルツの不等式を用いました。
以上から, d は距離関数になっており,確かに距離空間であることが分かりました。
例2.(平面におけるマンハッタン距離;L^1 距離)
\mathbb{R}^2 = \{ (x_1, x_2) \mid x_1, x_2 \in \mathbb{R} \} は, \boldsymbol{x} = (x_1,x_2), \boldsymbol{y} = (y_1, y_2) に対し,
\textcolor{red}{d(\boldsymbol{x}, \boldsymbol{y}) = |x_1 - y_1| + |x_2-y_2|}
と定めることで,距離空間になる。この距離をマンハッタン距離 (Manhattan distance) または L^1 距離という。
空間は同じですが,距離の入り方が違うことに注意しましょう。
たとえば, O(0, 0) , A(3, 4) の距離は,ユークリッド距離の場合は \sqrt{3^2 + 4^2} =5 ですが,マンハッタン距離の場合は |3| + |4| = 7 になります。
マンハッタン距離は,よく「京都の碁盤の目のような距離」と言われます。広大な野原の場合,2点を移動するのには直線で行けるため,ユークリッド距離が有用でしょう。一方で,碁盤の目のような地形の場合,直線では行けませんから,マンハッタン距離の方が有用だと言えます。
以下の図で,緑がユークリッド距離,赤がマンハッタン距離の行き方を模式的に表しています。
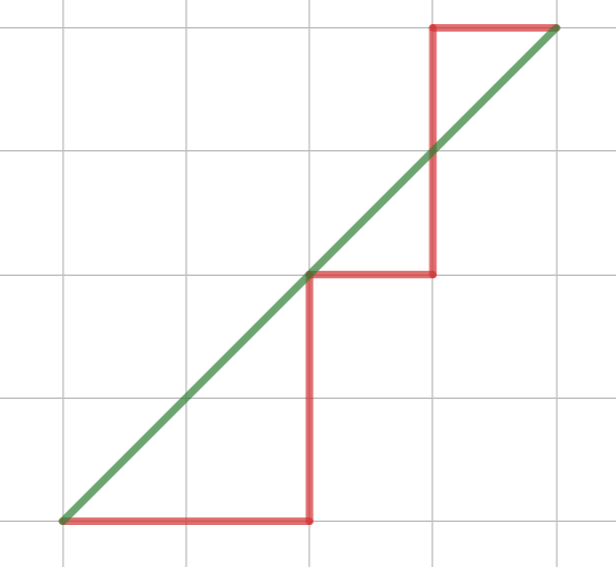
では,距離の定義をみたすか確認していきましょう。まず, d(\boldsymbol{x}, \boldsymbol{y}) = 0 \Leftrightarrow \boldsymbol{x} = \boldsymbol{y} と d(\boldsymbol{x}, \boldsymbol{y}) = d(\boldsymbol{y}, \boldsymbol{x}) が成立することはほぼ明らかでしょう。三角不等式については, \boldsymbol{x} = (x_1, x_2), \boldsymbol{y} = (y_1,y_2), \boldsymbol{z} = (z_1, z_2) に対し, a_i = x_i - y_i, b_i = y_i - z_i とおくと,
\begin{aligned} &d(\boldsymbol{x}, \boldsymbol{z})\\ &= |a_1+b_1| + |a_2+b_2| \\ &\le |a_1|+|b_1| + |a_2| + |b_2| \\ &= d(\boldsymbol{x}, \boldsymbol{y}) + d(\boldsymbol{y},\boldsymbol{z}) \end{aligned}であることから,結局距離空間であることが分かりました。
他の例も挙げましょう。
例3.(n次元空間上のユークリッド距離とマンハッタン距離)
\mathbb{R}^n = \{ (x_1,\ldots, x_n) \mid x_1, \ldots, x_n \in \mathbb{R} \} は, \boldsymbol{x} = (x_1,\ldots, x_n), \boldsymbol{y} = (y_1, \ldots, y_n) に対し,
\textcolor{red}{d(\boldsymbol{x}, \boldsymbol{y}) = \sqrt{\sum_{k=1}^n (x_k - y_k)^2} }
と定めると,これは距離空間となる。これをユークリッド距離( L^2 距離)という。
また,
\textcolor{red}{d(\boldsymbol{x}, \boldsymbol{y}) = \sum_{k=1}^n |x_k-y_k|}
と定めると,これも距離空間となる。これをマンハッタン距離(L^1 距離)という。
平面の場合の一般化ですね。距離空間であることの確認は,ほぼ同様なので省略します。
その他の例も挙げてみましょう。
例4.(チェビシェフ距離;L^\infty 距離)
\mathbb{R}^n = \{ (x_1,\ldots, x_n) \mid x_1, \ldots, x_n \in \mathbb{R} \} は, \boldsymbol{x} = (x_1,\ldots, x_n), \boldsymbol{y} = (y_1, \ldots, y_n) に対し,
\textcolor{red}{d(\boldsymbol{x}, \boldsymbol{y}) = \max_{1 \le k \le n} |x_k - y_k|}
と定めると,これは距離空間となる。
例5.(連続関数の最大値; L^\infty 距離)
[0,1] 上の連続関数の集合 C[0,1] = \{ f\colon [0,1] \to \mathbb{R} \mid f \text { is continuous} \} は, f, g \in C[0,1] に対し,
\textcolor{red}{d(f, g) = \sup_{0 \le x \le 1} |f(x) - g(x)| }
と定めることで距離空間となる。
例4と例5の証明は演習問題としましょう。
例6.(連続関数の積分;L^p 距離)
p \ge 1 とする。このとき, [0,1] 上の連続関数の集合 C[0,1] = \{ f\colon [0,1] \to \mathbb{R} \mid f \text { is continuous} \} は, f, g \in C[0,1] に対し,
\color{red} d(f, g) = \left(\int_0^1 |f(x) - g(x)|^p dx \right)^{1/p}
と定めることで距離空間となる(L^p 距離)。
この例は関数解析学において非常に重要ですが,これが距離空間になることを証明するのはかなり難しいため,そういうものだと思ってください。
他,離散距離も基本的かつ有名です。以下で解説しています。
さいごに
数学における「距離空間」の定義について確認しました。
距離空間の距離という「尺度」を用いて,主に極限や連続性といった解析的な話ができるようになります。大学数学においては必須の概念ですので,しっかり押さえておきましょう。