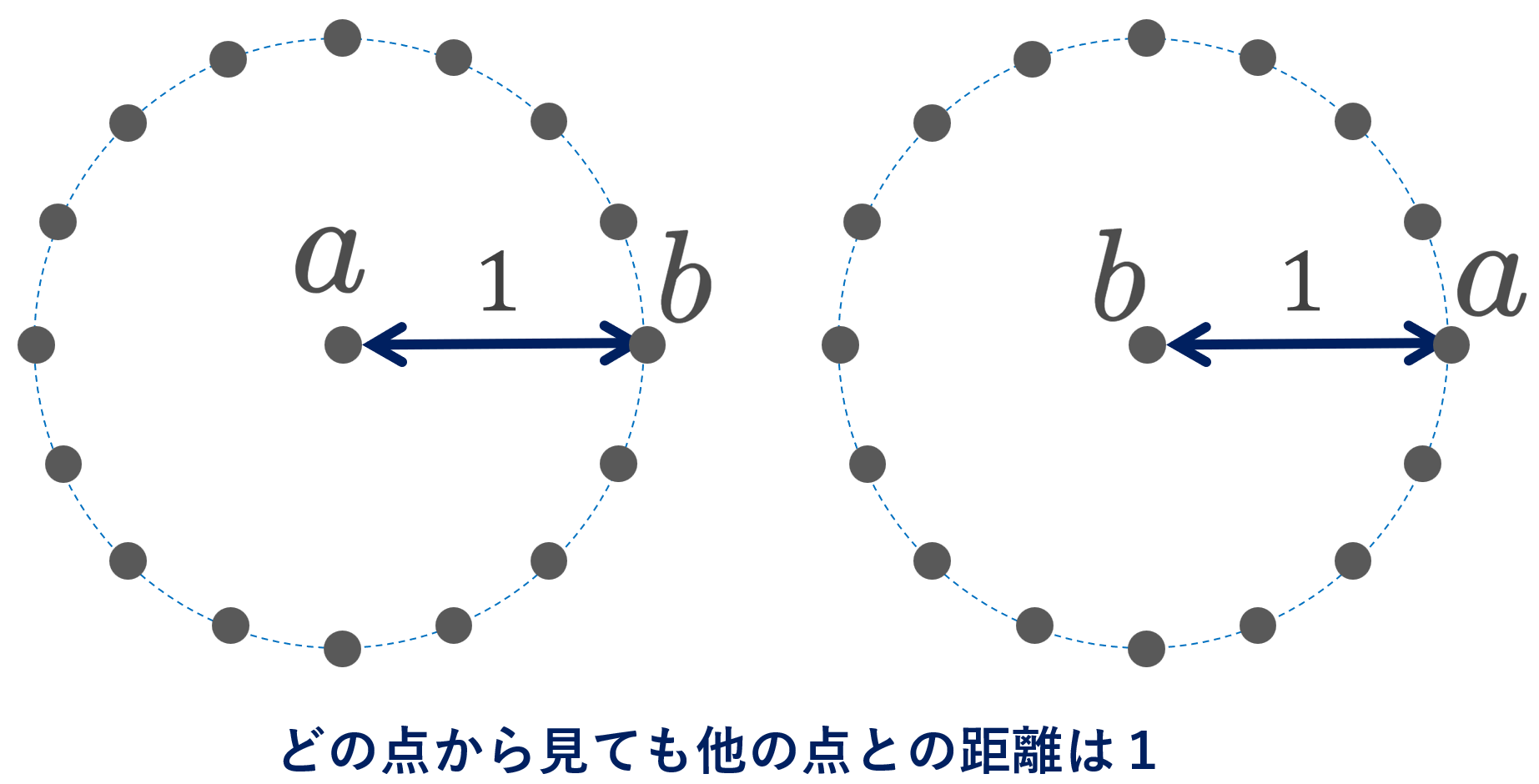
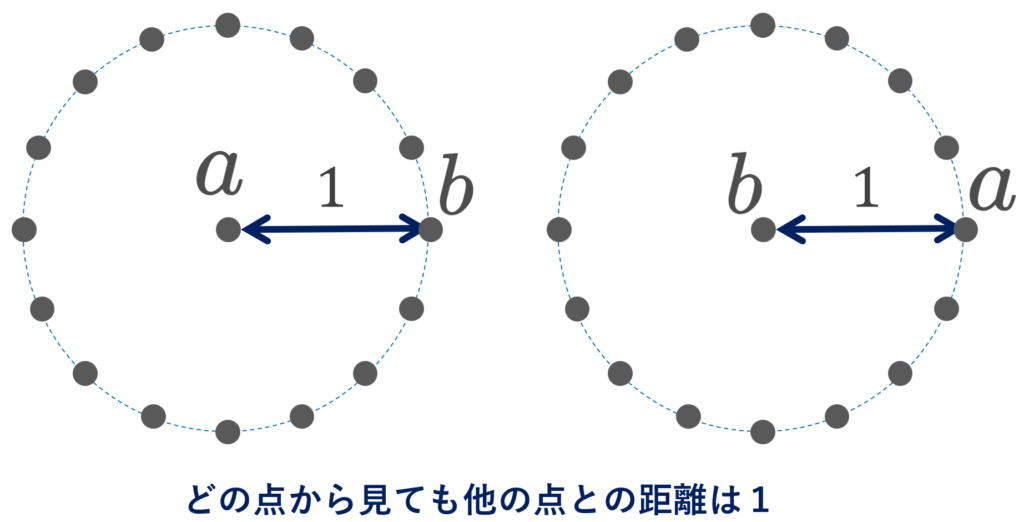
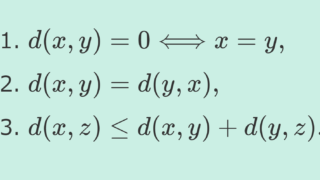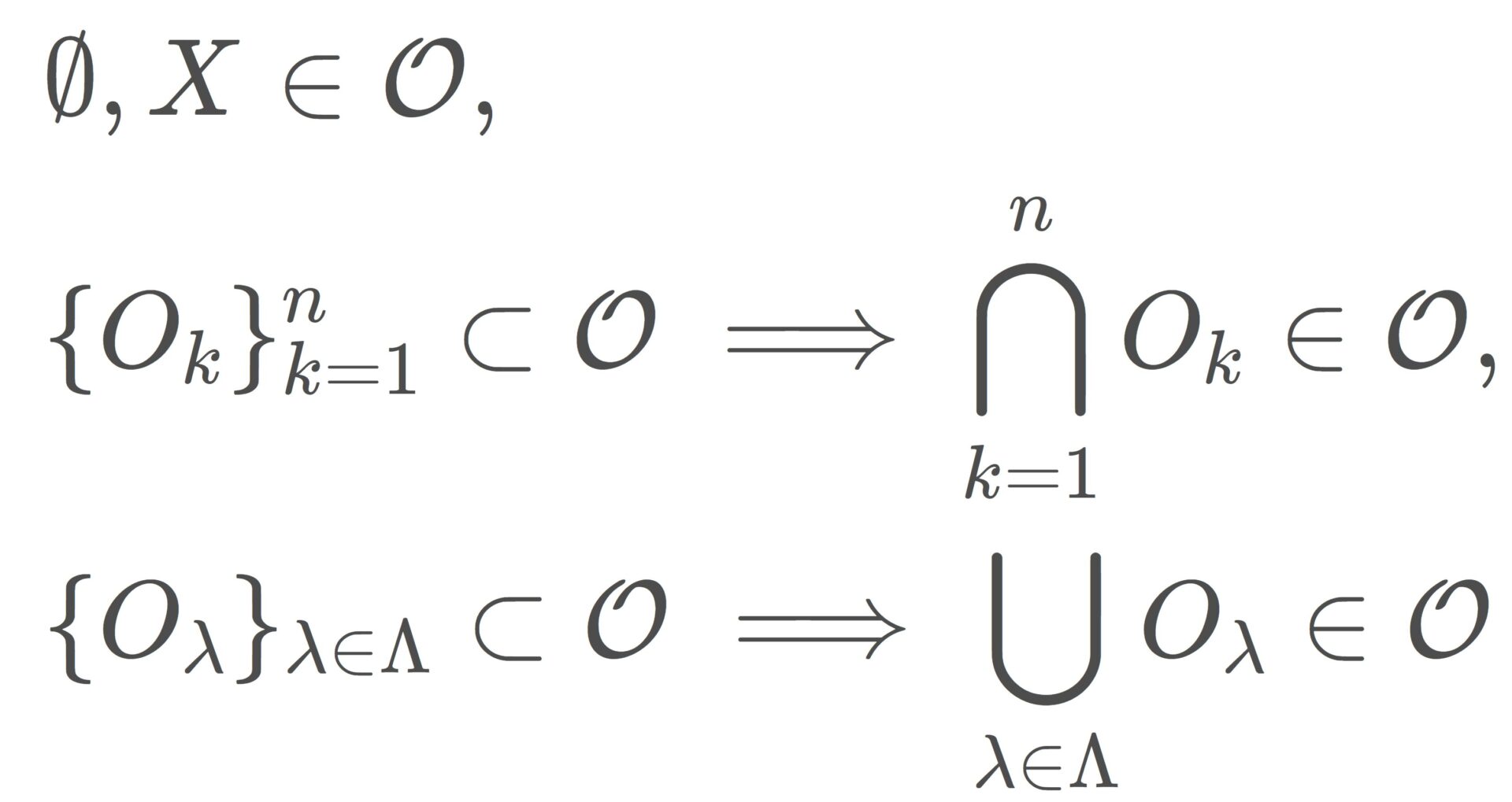離散距離空間とは～定義と性質～

離散距離空間とは，全ての点が離れているような空間です。ユークリッド空間とは全く違う空間ですが，距離空間における基本的な空間です。離散距離空間について，その定義と性質を解説しましょう。

離散距離空間の定義

定義（離散距離空間）

$X$ を空でない集合とする。

\Large \color{red} d(a,b) = \begin{cases} 0 & a=b, \\ 1& a\ne b \end{cases}

と定めると， $d$ は距離であり， $(X, d)$ は距離空間となる。これを離散距離空間 (discrete metric space) といい， $d$ を離散距離 (discrete metric) という。

離散距離空間のイメージは上の画像にかきましたが，平面上では正しくかけません。

距離空間の定義

今回の離散距離は，この定義をみたしますね。場合分けして確認すれば分かります。

定理1（離散距離空間と収束・完備性）

$(X, d)$ を離散距離空間とする。

数列 $\{x_n\}\subset X$ が $x\in X$ に収束するならば，ある $N\ge 1$ が存在して，

x_N=x_{N+1}=x_{N+2}=x_{N+3}=\cdots = x

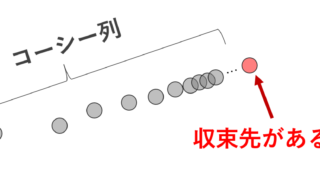
となる。また，離散距離空間は完備である。

離散距離空間はどの点も遠いので，収束するのであれば，いずれはずっと $x$ に一致するような数列でなければなりません。 $\{x_n\}$ が $x\in X$ に収束するならば，その定義より，ある $N\ge 1$ が存在して，

n\ge N\implies d(x_n, x)<\frac{1}{2}

とできます。離散位相空間なら $d(x_n, x)<1/2\implies x_n =x$ ですから，示せましたね。

また，離散距離空間は完備です。完備とは，任意のコーシー列が収束列になるようなものです。 $\{x_n\}\subset X$ がコーシー列であれば，コーシー列の定義より，ある $N\ge 1$ が存在して，

m,n \ge N\implies d(x_m, x_n)<\frac{1}{2}

とできなければなりません。離散距離空間なら $d(x_m, x_n)<1/2\implies x_m=x_n$ ですから，

m, n \ge N \implies x_m=x_n

であり，結局

x_N=x_{N+1}=x_{N+2}=x_{N+3}=\cdots

ということになります。 $\{x_n\}$ はいずれはずっと同じ値になる数列というわけです。よって収束列なので，離散距離空間は完備であると示せました。

定理2（離散距離空間と有界・全有界）

離散距離空間は有界である。また，離散距離空間 $(X, d)$ が全有界である必要十分条件は， $X$ が有限集合であることである。

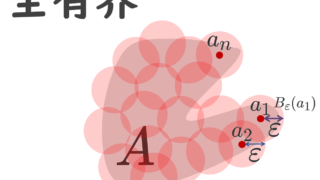
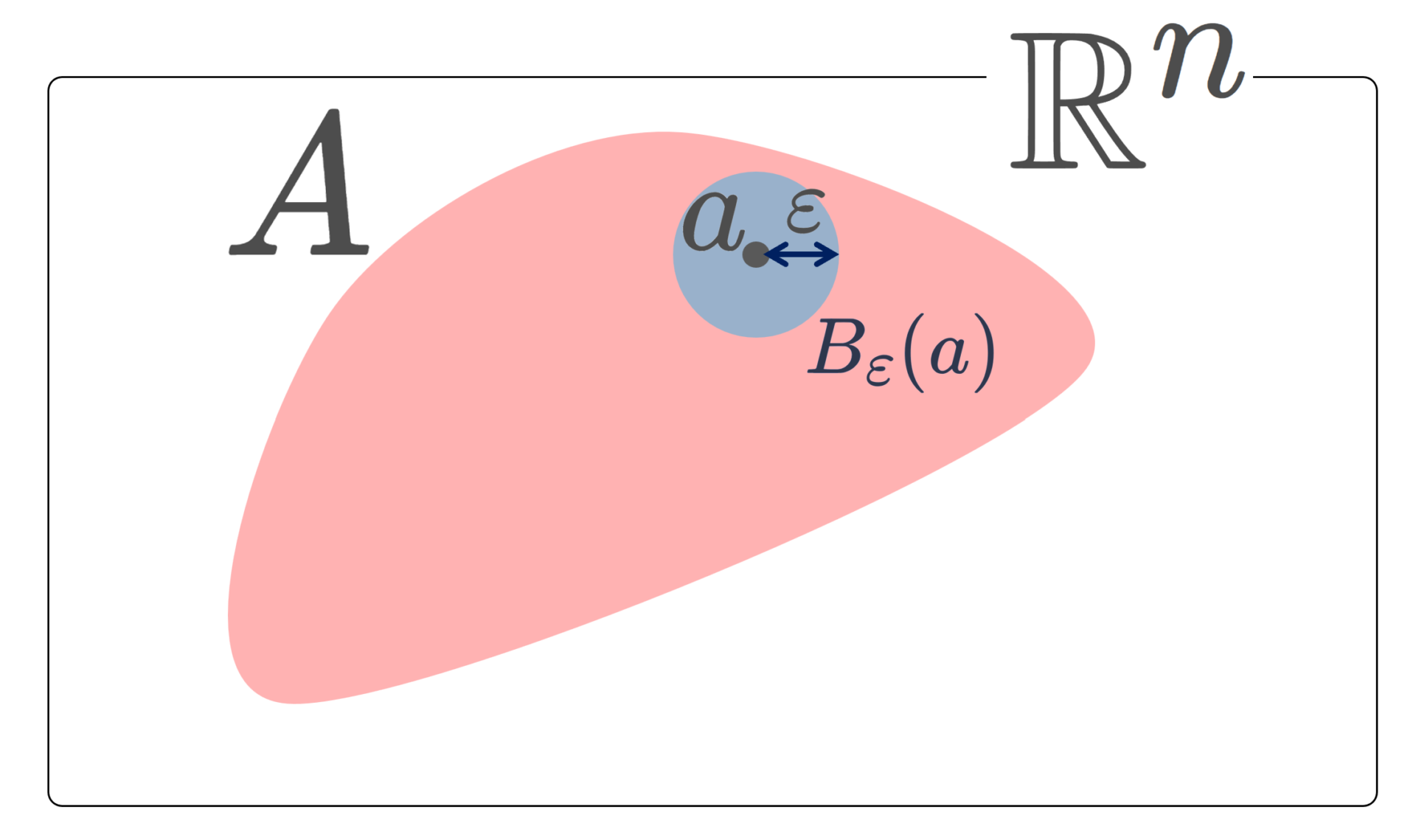
$B_\varepsilon(a)=\{ x\in X\mid d(a,x)<\varepsilon\}$ を $\varepsilon$ -近傍とすると， $a\in X$ に対し， $B_2(a)=X$ ですから， $X$ は有界です。

一方で， $B_{1/2}(a)=\{a\}$ ですから，有限個の $1/2$ -近傍で覆える必要十分条件は $X$ が有限集合であることです。

定理3（離散距離空間の位相的性質）

離散距離空間の誘導する位相は離散位相である。

誘導する位相とは，「距離空間における開集合族のなす位相」のことです。離散距離空間は，全ての部分集合が開集合になります。離散位相は，全ての部分集合が開集合であるような位相空間のことです。

離散距離空間の全ての部分集合が開集合になることを簡単に解説しておきましょう。離散距離空間では， $B_{1/2}(a)=\{a\}$ ですから， $A\subset X$ において，任意の $a\in A$ は

a\in B_{1/2}(a)\subset A

とできます。よって，任意の $a\in A$ は $A$ の内点ですから， $A$ の内部は $A$ 自身であり， $A$ は開集合です。よって，全ての部分集合が開集合です。