列ベクトルと行ベクトルの定義と違い

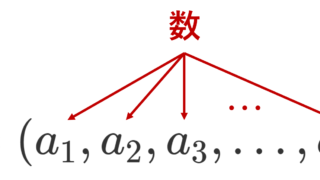
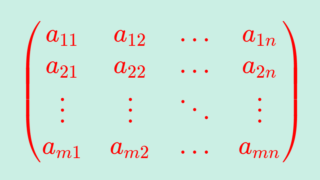$\overrightarrow{a}=\begin{pmatrix} 2\\ 3\end{pmatrix}$ のように数を縦に複数個並べたものを「列ベクトル」， $\overrightarrow{a}=(2,3)$ のように数を横に並べたものを「行ベクトル」といいます。

列ベクトルと行ベクトルについて，その定義と基本的な違いを解説しましょう。

列ベクトルと行ベクトル
列ベクトルと行ベクトルの違い
数ベクトル
関連する記事

列ベクトルと行ベクトル

定義（列ベクトル・行ベクトル）

$n$ 個の数 $a_1,a_2,\dots, a_n$ を縦に並べた

\large \color{red} \overrightarrow{a}= \begin{pmatrix} a_1\\a_2\\ \vdots \\ a_n \end{pmatrix}

を $n$ 次元列ベクトルといい，横に並べた

\large \color{red} \overrightarrow{a}=(a_1,a_2,\dots, a_n)

を $n$ 次元行ベクトルという。

たとえば， $\begin{pmatrix} 2\\ 3\end{pmatrix}$ や $\begin{pmatrix} 2 \\ -3\\ 1\end{pmatrix}$ はどちらも列ベクトルであり， $(1,5)$ や $(0, -2, 3)$ は行ベクトルです。

なお，高校まではベクトルは矢印をつけて表すことが多いですが，大学では $\boldsymbol{a}$ のように太字で表したり，文脈上明らかなときは単に $a$ とかくこともあります。

列ベクトルと行ベクトルの違い

たとえば高校生が，幾何的な向きと大きさを表すのにベクトルを使うのであれば，列ベクトルと行ベクトルの違いはないと言っていいでしょう。どちらを用いても構いません。（ただし，列ベクトルと行ベクトルを混ぜないでください。）

列ベクトルと行ベクトルの違いが出るのは，それを行列として捉えるときです。

列ベクトル $\overrightarrow{a}= \begin{pmatrix} a_1\\a_2\\ \vdots \\ a_n \end{pmatrix}$ は， $n\times 1$ 行列と見ることが可能で，行ベクトル $\overrightarrow{a}=(a_1,a_2,\dots, a_n)$ は $1\times n$ 行列と見ることができます。（ $\begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{pmatrix}$ が $m\times n$ 行列です）

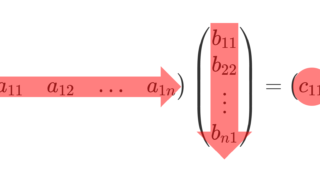
行列とベクトルの演算は，行列同士の演算と考えて演算を行います。この際，特に積の演算では，行列に列ベクトルをかけるか行ベクトルをかけるかによって，異なる意味を持ちます。
たとえば， $n\times n$ 行列 $A$ に対し， $A\overrightarrow{x}$ は，