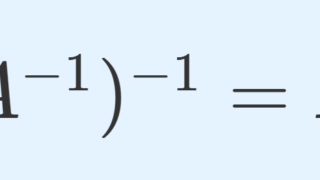逆行列の定義と2通りの求め方～計算の手順～

正方行列における，逆行列の定義と，その計算方法2通りを，手順を追って解説します。

逆行列の定義
逆行列の2通りの求め方～計算の手順～
関連記事

逆行列の定義

定義（逆行列）

$A$ を正方行列とし， $I$ を同じ大きさの単位行列とする。このとき，

\color{red} AA^{-1} = A^{-1} A = I

が成り立つような正方行列 $\color{red} A^{-1}$ が存在するとき，これを $A$ の逆行列 (inverse of the matrix) という。

行列の積における「逆元」といえるので，逆行列という名前がついているんですね。

注意ですが， $A$ を正方行列としたとき，必ず逆行列があるとは限りません。たとえば，零行列 $O$ には逆行列が存在しません。逆行列が存在するような正方行列のことを，正則行列 (invertible matrix) といいます。
それじゃあ「どのような行列が正則になるか」ということを疑問に思ったかもしれません。これについては，また別の機会に解説したいと思います。

正則行列の性質については，以下の記事で解説しています。

一つだけ，例を紹介します。

2次正方行列の逆行列

$2$ 次の正方行列 $A= \begin{pmatrix} a& b \\ c& d \end{pmatrix}$ は $ad-bc\ne 0$ のとき，逆行列が存在し，

\color{red}A^{-1} = \frac{1}{ad-bc}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix}

となる。

2次正方行列の逆行列は覚えるのみです。丸暗記してしまうのが速いと思います。実際にそうなるかは，計算で確認してみましょう。

逆行列の2通りの求め方～計算の手順～

逆行列の具体的な計算の手順について，余因子行列を用いた計算

掃き出し法による計算
余因子行列を用いた計算

の2つを確認していきましょう。

1. 掃き出し法による計算

まずは，大変有用な「掃き出し法による計算」を確認しましょう。

定理（掃き出し法）

$A$ を逆行列が存在する $n$ 次行列(正則行列)とし， $I$ を $n$ 次単位行列とする。

このとき，この２つを並べてできた $n\times 2n$ 行列 $\color{red} (A, I )$ を，行に関する基本変形のみを用いて $\color{red} (I, A^{-1})$ の形にする。

このときの $A^{-1}$ は $A$ の逆行列である。

行に関する基本変形とは，以下の３つの操作のことです。

行に関する基本変形

ある行の $\boldsymbol{c}$ 倍を他の行に加えること
2つの行を入れ替えること
ある行を $\boldsymbol{ c \ne 0 }$ 倍すること

行に関する基本変形とは，基本行列を左からかけることに相当しますから，左からかけた基本行列の積が，結局 $A^{-1}$ になるため，これが成立します。

行列の基本変形について詳しくは，以下の記事を参照してください。

さて，これを踏まえて，次の例題を解いてみましょう。

例題1

$A=\begin{pmatrix}1&0&2 \\-1& 2 & 2 \\ 1 & 2 & 0\end{pmatrix}$ の逆行列を，掃き出し法を用いて計算せよ。

横長の行列 $\begin{pmatrix} 1&0&2 & 1 & 0 & 0 \\-1& 2 & 2 & 0 & 1 & 0 \\ 1 & 2 & 0 & 0 & 0 & 1 \end{pmatrix}$ を考えて，その左側 $\begin{pmatrix}1&0&2 \\-1& 2 & 2 \\ 1 & 2 & 0\end{pmatrix}$ が $I$ になるように，行に関する基本変形を行えばよいのですね。

計算例を挙げると，以下のようになります。もちろん，これ以外の計算でも構いません。左側の対角成分(ナナメ)が $1$ に，それ以外が $0$ になるように変形します。

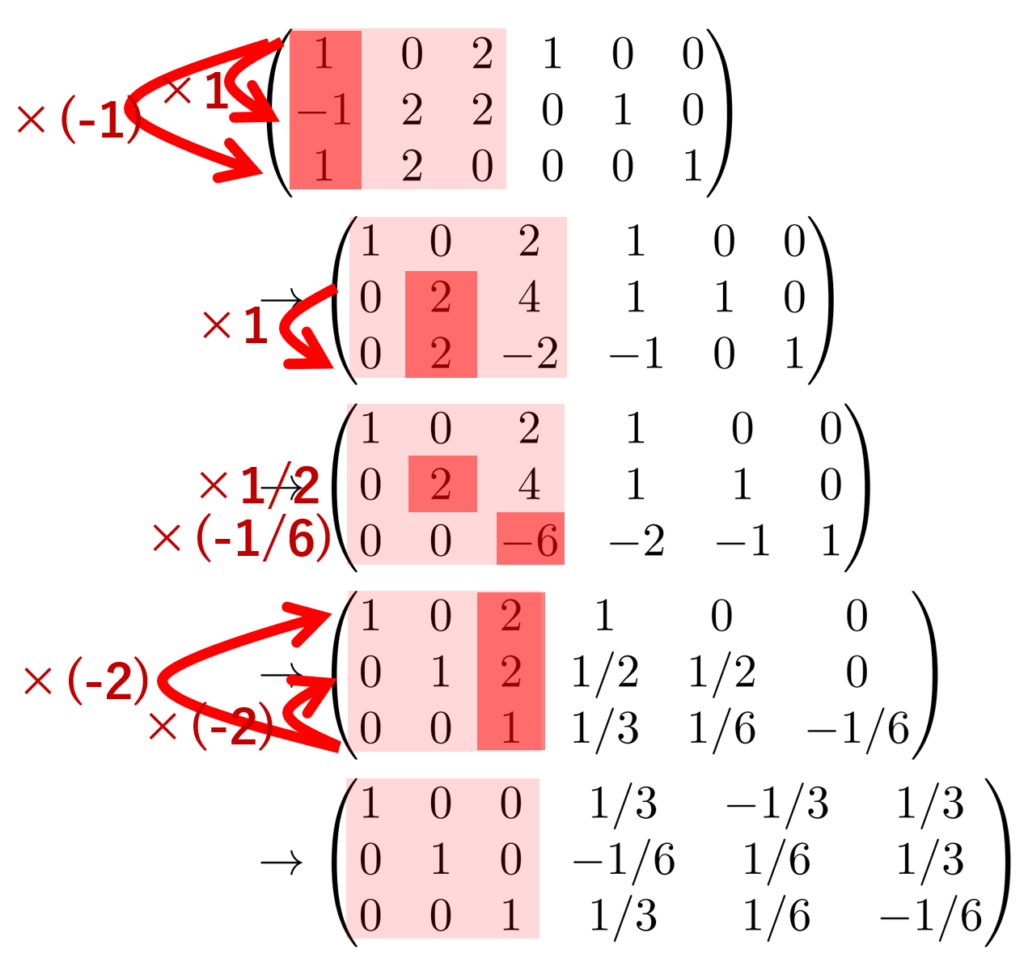
よって，求める逆行列は

\begin{pmatrix}1/3&-1/3&1/3\\-1/6&1/6&1/3\\1/3&1/6&-1/6  \end{pmatrix}

になります。

2. 余因子行列を用いた計算

こちらは，1の「掃き出し法による計算」よりも計算が煩雑になりがちなので，おまけ的なポジションです。掃き出し法を理解していれば，こちらはマスターしなくても構いません。

まずは余因子行列が何か，確認しましょう。

定義（余因子行列）

$n$ 次正方行列

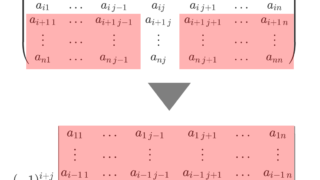
\scriptsize\begin{pmatrix} a_{11} & \dots & a_{1\,j-1} & a_{1j} & a_{1\,j+1} &\dots & a_{1n} \\ \vdots & \cdots & \vdots & \vdots & \vdots & \dots & \vdots \\ a_{i-1\,1} & \dots & a_{i-1\,j-1} & a_{i-1\,j} & a_{i-1\,j+1} &\dots & a_{i-1\,n}\\ a_{i1} & \dots & a_{i\,j-1} & a_{ij} & a_{i\,j+1} &\dots & a_{in} \\ a_{i+1\,1} & \dots & a_{i+1\,j-1} & a_{i+1\,j} & a_{i+1\,j+1} &\dots & a_{i+1\,n}\\ \vdots & \cdots & \vdots & \vdots & \vdots & \dots & \vdots \\ a_{n1} & \dots & a_{n\,j-1} & a_{nj} & a_{n\,j+1} &\dots & a_{nn} \end{pmatrix}

に対し，その $i$ 行と $j$ 列を除いた $n-1$ 次正方行列の行列式の $(-1)^{i+j}$ 倍

\scriptsize (-1)^{i+j}\begin{vmatrix} a_{11} & \dots & a_{1\,j-1} & a_{1\,j+1} &\dots & a_{1n} \\ \vdots & \cdots & \vdots & \vdots & \dots & \vdots \\ a_{i-1\,1} & \dots & a_{i-1\,j-1} & a_{i-1\,j+1} &\dots & a_{i-1\,n}\\ a_{i+1\,1} & \dots & a_{i+1\,j-1} & a_{i+1\,j+1} &\dots & a_{i+1\,n}\\ \vdots & \cdots & \vdots & \vdots & \dots & \vdots \\ a_{n1} & \dots & a_{n\,j-1} & a_{n\,j+1} &\dots & a_{nn} \end{vmatrix}

を $(i,j)$ 余因子 (cofactor) という。

$A$ を $n$ 次正方行列とし， $\tilde{a}_{ij}$ をその $(i,j)$ 余因子とする。このとき， $\color{red} \tilde{A} = (\tilde{a}_{ij})^\top = (\tilde{a}_{ji})$ を余因子行列 (adjugate matrix) という。

このとき，以下の定理が成立します。

定理（余因子行列と逆行列）

$A$ を正則行列とする。このとき，