余因子・余因子行列の定義と余因子展開について図解付きで述べ,余因子行列が逆行列の行列式倍になることの証明を行いましょう。
余因子・余因子行列の定義
まずは,余因子と余因子行列の定義を述べましょう。
余因子の定義
定義(余因子)
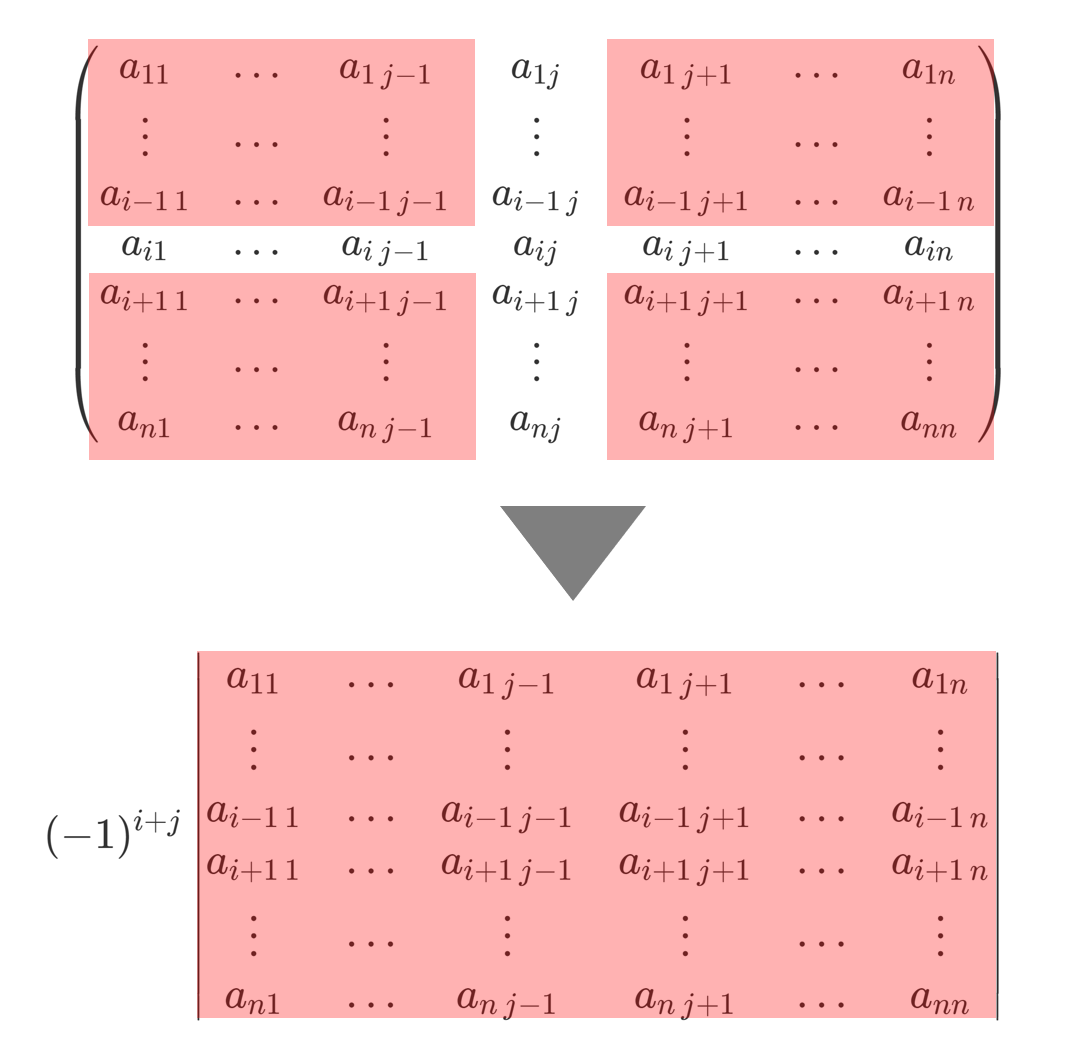
n 次正方行列
\scriptsize\begin{pmatrix} a_{11} & \dots & a_{1\,j-1} & a_{1j} & a_{1\,j+1} &\dots & a_{1n} \\ \vdots & \cdots & \vdots & \vdots & \vdots & \cdots & \vdots \\ a_{i-1\,1} & \dots & a_{i-1\,j-1} & a_{i-1\,j} & a_{i-1\,j+1} &\dots & a_{i-1\,n}\\ a_{i1} & \dots & a_{i\,j-1} & a_{ij} & a_{i\,j+1} &\dots & a_{in} \\ a_{i+1\,1} & \dots & a_{i+1\,j-1} & a_{i+1\,j} & a_{i+1\,j+1} &\dots & a_{i+1\,n}\\ \vdots & \cdots & \vdots & \vdots & \vdots & \cdots & \vdots \\ a_{n1} & \dots & a_{n\,j-1} & a_{nj} & a_{n\,j+1} &\dots & a_{nn} \end{pmatrix}
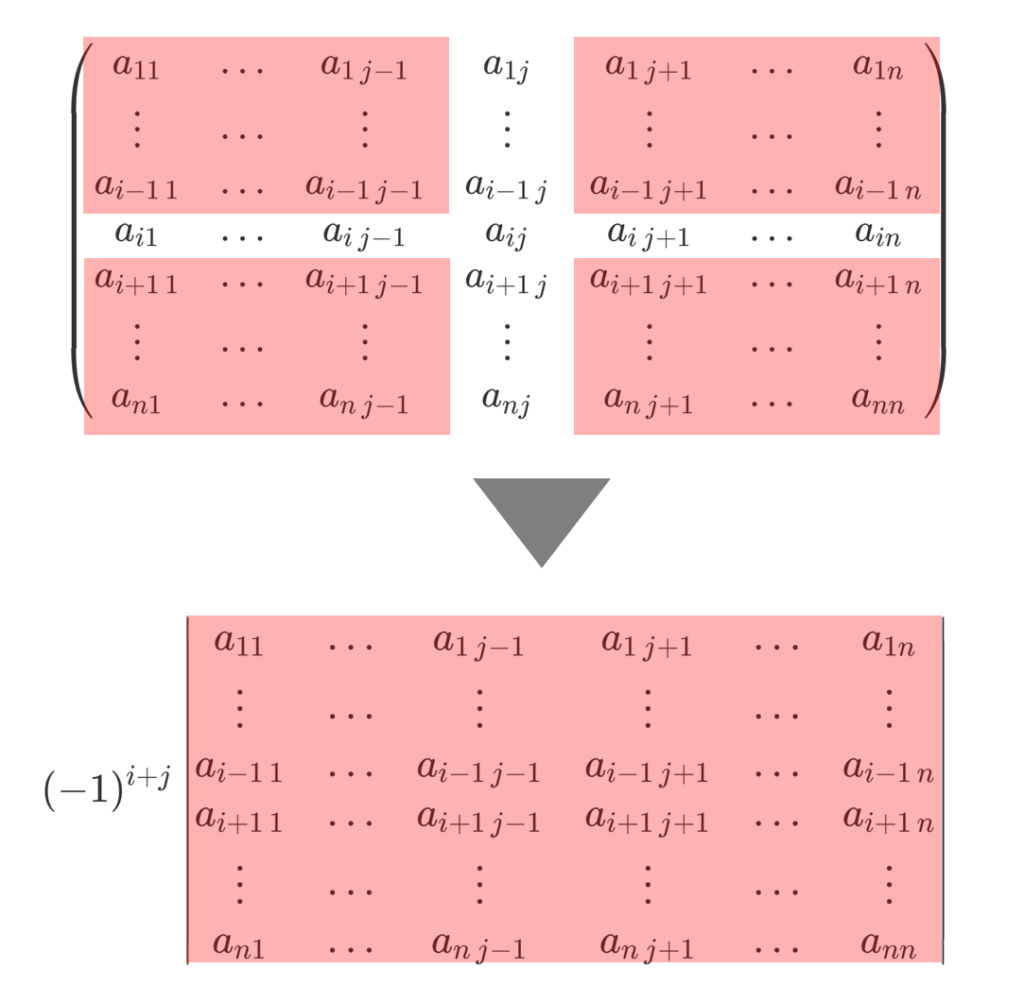
に対し,その i 行と j 列を除いた n-1 次正方行列の行列式の (-1)^{i+j} 倍
を (i,j) 余因子 (cofactor) という。
「 i 行と j 列を除いた」の部分をわかりやすく図解すると,以下のようになります。
余因子はただの「数」であって行列ではありません。
余因子を求めるには,行列式の計算が必要になります。これについては,以下で解説しています。
余因子行列の定義
定義(余因子行列)
A を n 次正方行列とし, \tilde{a}_{ij} をその (i,j) 余因子とする。このとき,\color{red} \tilde{A} = (\tilde{a}_{ij})^\top = (\tilde{a}_{ji}) を余因子行列 (adjugate matrix) という。
(i,j) 余因子を (i,j) 成分に据えた行列を考え,その行列の転置を取ったもの(転置行列)が余因子行列なわけですね。
行列式の余因子展開
余因子展開とは,もとの行列の行列式を余因子を用いて展開することです。以下の定理を証明しましょう。
定理(余因子展開)
A を n 次正方行列とし, \tilde{a}_{ij} をその (i,j) 余因子とする。このとき, 1\le k \le n に対し,
\color{red}\begin{aligned}\det A &= a_{k1} \tilde{a}_{k1} + a_{k2} \tilde{a}_{k2} +\dots + a_{kn}\tilde{a}_{kn} \\ &= a_{1k} \tilde{a}_{1k} + a_{2k} \tilde{a}_{2k} +\dots + a_{nk}\tilde{a}_{nk}. \end{aligned}
また, k \ne l とすると,
も成立する。
余因子展開を図にすると,以下のようになります。
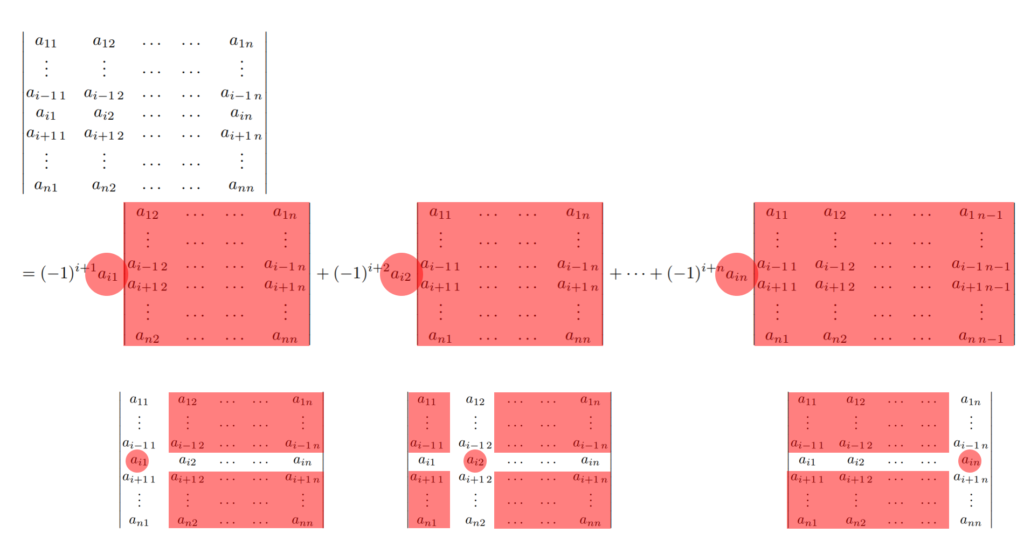
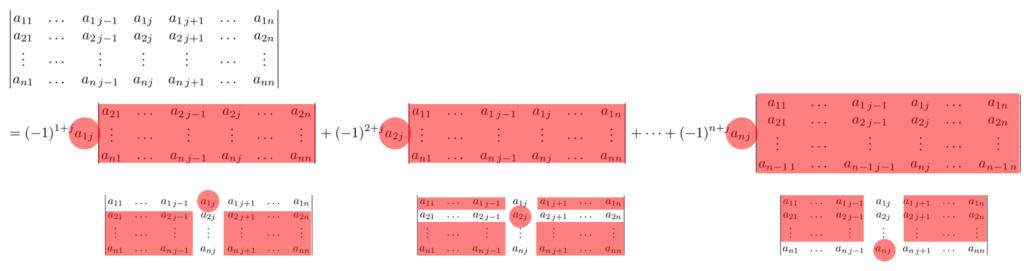
行列式を,より小さな行列式の演算で書き表しているといえますね。
早速証明しましょう。
証明
\begin{aligned}\det A &= a_{k1} \tilde{a}_{k1} + a_{k2} \tilde{a}_{k2} +\dots + a_{kn}\tilde{a}_{kn}\end{aligned} について
\det A の定義式を a_{kj} \;\;(1\le j\le n) に着目して整理すると, a_{kj} の係数は, A の第 k 行を \begin{pmatrix}0 & \dots& 0 &1& 0& \dots &0 \end{pmatrix} (第 j 列のみ 1 ) としたものに等しく,それは \tilde{a}_{kj} に等しい。
2つ目の等式も同様である。(あるいは, A^\top (転置行列) で考えて,上を適用してもよい。)
\begin{aligned} 0 &= a_{k1} \tilde{a}_{l1} + a_{k2} \tilde{a}_{l2} +\dots + a_{kn}\tilde{a}_{ln} \end{aligned} について
前半の証明より,この右辺は A の第 l 行を \begin{pmatrix} a_{k1} & \dots & a_{kn} \end{pmatrix} に置き換えた行列 B の行列式に等しい。 B の第 k 行と第 l 行は同じであり,同じ行の存在する行列式の値は0であるから, \det B = 0 である。
2つ目の等式も同様である。(あるいは, A^\top (転置行列) で考えて,上を適用してもよい。)
証明終
余因子行列と逆行列
余因子行列と逆行列は,ほぼ同様のものと言えます。それが,以下の定理です。
余因子行列を用いれば,逆行列が求まるということですね。
これの証明は,先程の定理と行列の積の定義から, \tilde{A}A = A\tilde{A} = (\det A)I となるため,明らかでしょう。