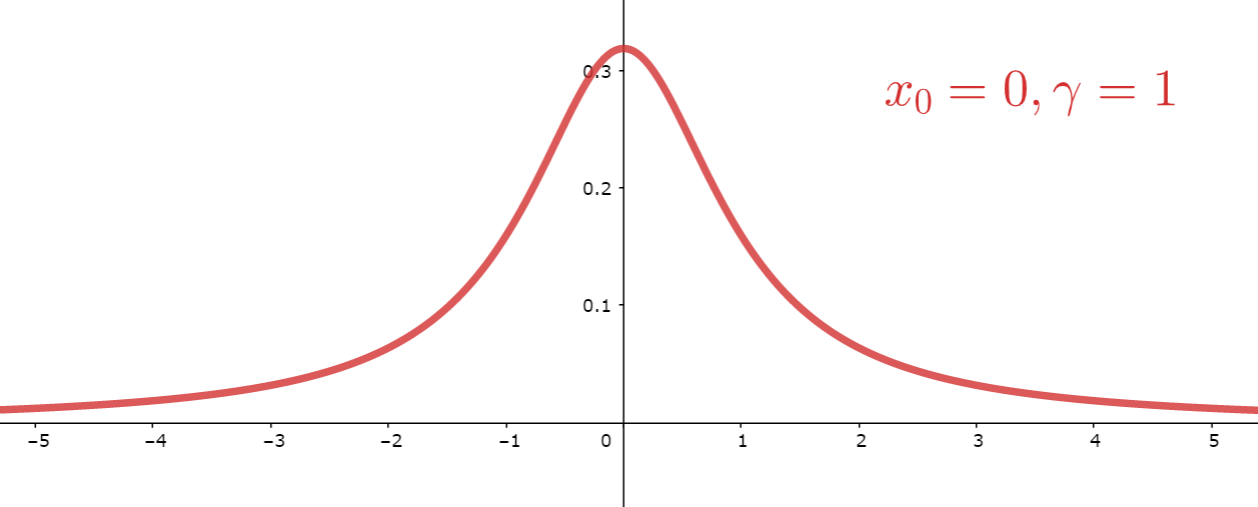
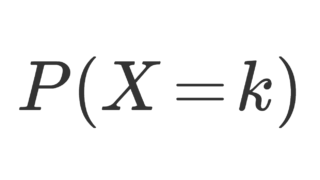コーシー分布の定義と性質とその証明

コーシー分布は，期待値が定義できず，正規分布より減衰が遅い，裾の厚い分布（裾の重い分布）として有名です。確率密度関数は $p(x) = \dfrac{1}{\pi(x^2+1)}$ となります。これについて，その定義と性質の証明を詳しく述べましょう。

コーシー分布の定義
コーシー分布の性質とその証明
その他の確率分布

コーシー分布の定義

定義（コーシー分布）

$X$ を確率変数とする。 $X$ の確率密度関数 $p(x)$ が，パラメータ $x_0 \in \mathbb{R},\; \gamma> 0$ として

\color{red} p(x) =\frac{\gamma}{\pi\{(x-x_0)^2 +\gamma^2\}}

となるとき， $X$ はコーシー分布 (Cauchy distribution) に従うという。特に， $x_0=0, \; \gamma =1$ とした

\color{red} p(x) = \frac{1}{\pi(x^2+1)}

を標準コーシー分布 (standard Cauchy distribution) という。

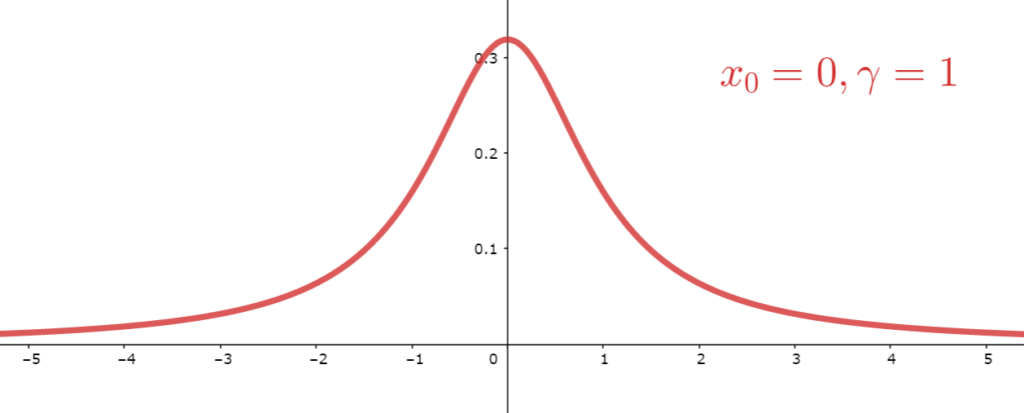
まず，

\begin{aligned} &P(X\in (-\infty, \infty))\\ &= \int_{-\infty}^\infty p(x)\, dx \\ &= \int_{-\infty}^\infty \frac{\gamma}{\pi\{(x-x_0)^2 +\gamma^2\}}\, dx \\ &= \int_{-\infty}^\infty \frac{\gamma}{\pi(y^2 +\gamma^2)} \, dy \\ &= \frac{1}{\pi}\left[ \tan^{-1} \frac{y}{\gamma} \right]_{-\infty}^\infty = 1 \end{aligned}

となるので，ちゃんと確率の合計は $1$ になっていますね。ここで， $\tan^{-1}$ は $\tan$ の逆関数です(→逆三角関数(arcsin,arccos,arctan)の定義と諸性質まとめ)。

$x_0=0$ とし， $\gamma$ を変えたときの，コーシー分布の確率密度関数のグラフの変化は，以下のようになります。また，比較のため，標準正規分布 $N(0,1)$ の確率密度関数も載せました。

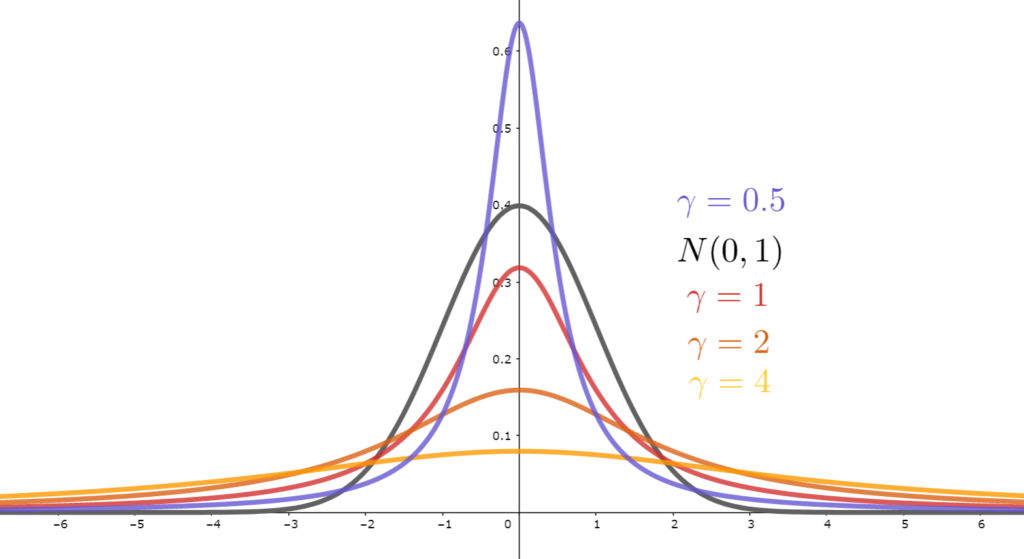
見ての通り，正規分布に比べて，コーシー分布の方が， $0$ から遠いところでの減衰が遅く，裾の厚い分布 (heavy tailed) になっています。これは，正規分布の確率密度関数が指数的に減衰するのに対し，コーシー分布は $x^{-2}$ 程度の減衰のため，減衰が遅いわけです。

コーシー分布の性質とその証明

まずは，今回考えるコーシー分布の性質を列挙しましょう。標準コーシー分布のときも添えることにします。

	コーシー分布	標準コーシー分布
確率の型	連続型	連続型
確率密度関数 $p(x)$	$\dfrac{\gamma}{\pi\{(x-x_0)^2 +\gamma^2\}}$	$\dfrac{1}{\pi(x^2+1)}$
累積分布関数 $F(x) = P(X\le x)$	$\dfrac{1}{\pi}\tan^{-1}\left(\dfrac{x-x_0}{\gamma}\right) + \dfrac{1}{2}$	$\dfrac{1}{\pi}\tan^{-1} x + \dfrac{1}{2}$
期待値(平均) $E[X]$	定義されない	定義されない
分散 $V(X)$	定義されない	定義されない
積率母関数 $E[e^{tX}]$	$\begin{cases} 1 & t=0, \\ \infty & t\ne 0 \end{cases}$	$\begin{cases} 1 & t=0, \\ \infty & t\ne 0 \end{cases}$
特性関数 $E[e^{itX}]$	$\exp(i x_0 t-\gamma \|t\|)$	$e^{-\|t\|}$

順番に考えていきましょう。

コーシー分布の累積分布関数(分布関数)

定理（コーシー分布の累積分布関数）

コーシー分布の累積分布関数(分布関数)は，

F(x) = \dfrac{1}{\pi}\tan^{-1}\left(\dfrac{x-x_0}{\gamma}\right) + \dfrac{1}{2}

である。ただし， $\tan^{-1}$ は $\tan$ の逆関数である(→逆三角関数(arcsin,arccos,arctan)の定義と諸性質まとめ)。

証明

累積分布関数(分布関数)とコーシー分布の定義より，

\begin{aligned} F(x) &= P(X\le x) = \int_{-\infty}^x p(x)\, dx \\ &= \frac{1}{\pi}\int_{-\infty}^x \frac{\gamma}{(x-x_0)^2 +\gamma^2}\,dx \\ &=\frac{1}{\pi} \int_{-\infty}^{x-x_0} \frac{\gamma}{x^2 +\gamma^2}\,dx \\ &=\frac{1}{\pi} \left[ \tan^{-1} \frac{x}{\gamma} \right]_{-\infty}^{x-x_0} \\ &= \dfrac{1}{\pi}\tan^{-1}\left(\dfrac{x-x_0}{\gamma}\right) + \dfrac{1}{2}. \end{aligned}

証明終

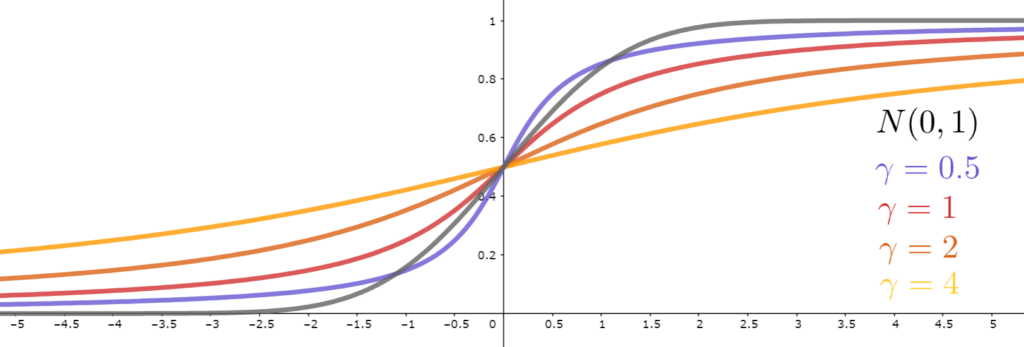
$x_0=0$ とし， $\gamma$ を変化させたときの累積分布関数のグラフは以下のようになります。比較のため，標準正規分布 $N(0,1)$ の累積分布関数も載せています。

コーシー分布は期待値(平均)・分散が定義されない

コーシー分布が最も特徴的な点は，期待値(平均)・分散が定義されないことです。よって，期待値・分散の存在を前提とする，大数の法則や中心極限定理も使えません。期待値・分散が定義されないことを，順番に確認していきましょう。

期待値(平均)が定義されないことの確認

コーシー分布の期待値(平均)が定義されないことを確認しましょう。これを確認するには，広義積分

\small E[X]=\int_{-\infty}^\infty xp(x)\, dx = \int_{-\infty}^\infty \frac{\gamma x}{\pi((x-x_0)^2+\gamma^2)}\, dx

が定義されないことを確認すればよいです。 $a,b>0$ を十分大きい数としましょう。このとき，

\small\begin{aligned} &\int_{-a}^b \frac{\gamma x}{\pi((x-x_0)^2+\gamma^2)}\, dx \\ &= \int_{-a-x_0}^0 \frac{\gamma y}{\pi(y^2+\gamma^2)}\, dy + \int_0^{b-x_0} \frac{\gamma y}{\pi(y^2+\gamma^2)}\, dy \\ &= \frac{\gamma}{2\pi} \left[\log(y^2+\gamma^2)\right]_{-a-x_0}^0 + \frac{\gamma}{2\pi} \left[\log(y^2+\gamma^2)\right]_{0}^{b-x_0} \\ &= \frac{\gamma}{2\pi}(\log((b-x_0)^2+\gamma^2) - \log((-a-x_0)^2+\gamma^2)) \end{aligned}

ですから， $a,b$ を独立に $a,b \to\infty$ とすると，

\int_{-\infty}^\infty \frac{\gamma x}{\pi((x-x_0)^2+\gamma^2)}\, dx =\infty-\infty

ですから，積分が収束せず，定義されません。そもそも， $E[X]$ は $E[|X|]<\infty$ でないと定義されません。今の場合， $E[|X|] =\infty$ になるので，コーシー分布の期待値(平均)は定義できないわけです。

正規分布はちゃんと期待値が定義できたわけですから，コーシー分布は，正規分布より裾が重く，広がりが大きいことが，このことからも分かります。実際， $|X|$ が大きい値を取る確率が高いから，うまく期待値が定義できないわけですよね。

分散が定義されないことの確認

分散の定義は，そもそも $V(X)=E[(X-E[X])^2 ]$ で，定義の中に $E[X]$ が含まれていますね。いま期待値が存在しないことから，分散も定義できないことがわかります。

コーシー分布の積率母関数(モーメント母関数)・特性関数

つづいて，コーシー分布の積率母関数(モーメント母関数)・特性関数を考えましょう。

定理（コーシー分布の積率母関数・特性関数）

コーシー分布の積率母関数(モーメント母関数)・特性関数はそれぞれ

\color{red} \begin{aligned} E[e^{tX}] &=\begin{cases} 1 & t=0, \\ \infty & t\ne 0 ,\end{cases} \\ E[e^{itX}] &= \exp(i x_0 t-\gamma |t|) \end{aligned}

である。

積率母関数は基本的に $\infty$ になりますから，定義されないようなものですね。一方で， $E[|e^{itX}|] = E[1] = 1$ ですから，特性関数は定義可能です。

特性関数の導出証明には，複素関数論の知識が必要になります。確認していきましょう。

証明

積率母関数について， $t\ne 0$ とする。 $a>0$ を十分大きくとると， $x\ge a \implies e^{|tx|} \ge x$ であることから，

\begin{aligned} E[e^{tX}] &\ge \min \bigl\{E[|X| 1_{\{X>a\}}], E[|X| 1_{\{X<-a\}}] \bigr\} \\ &=\infty\end{aligned}

となるため，従う。

特性関数について，求めるべきは，

\begin{aligned}E[e^{itX}] &= \int_{-\infty}^\infty e^{itx}p(x)\, dx \\ &= \int_{-\infty}^\infty e^{itx}\frac{\gamma}{\pi\{(x-x_0)^2 +\gamma^2\}} \, dx \\ &= e^{ix_0t} \int_{-\infty}^\infty \frac{\gamma e^{ixt}}{\pi(x^2+\gamma^2)} \, dx\end{aligned}

の値である。 $t> 0$ としよう。ここで，複素平面上で以下の図のような周回積分 $\displaystyle \int_{C_R} \frac{\gamma e^{izt}}{z^2+\gamma^2} \, dz$ を考える。

\small \begin{aligned} &\int_{C_R} \frac{\gamma e^{izt}}{z^2+\gamma^2} \, dz \\ &= \int_{-R}^R \frac{\gamma e^{ixt}}{x^2+\gamma^2} \, dx +\int_0^\pi \frac{\gamma Rie^{itR(\cos\theta+i\sin\theta)}}{(Re^{i\theta})^2+\gamma^2} \, d\theta \end{aligned}

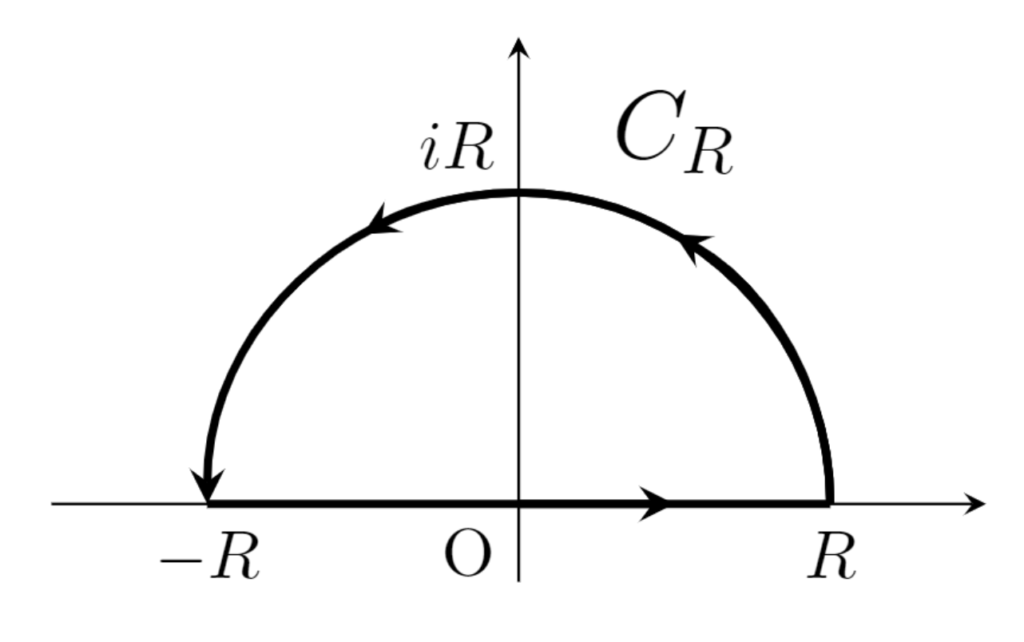
である( $\text{\textbf{(1)}}$ 式とする)。 $\dfrac{\gamma e^{izt}}{z^2+\gamma^2}$ は $z = \pm \gamma i$ で一位の零点を持つから， $R>0$ が十分大きいとき，留数定理より，

\begin{aligned} \int_{C_R} \frac{\gamma e^{izt}}{z^2+\gamma^2} \, dz &= 2\pi i \operatorname{Res} (f, \gamma i) \\ &= 2\pi i \lim_{z\to \gamma i} (z-\gamma i) \frac{\gamma e^{izt}}{z^2+\gamma^2} \\ &= \pi e^{-\gamma t}. \end{aligned}

また，

\begin{aligned} &\left|\int_0^\pi \frac{\gamma Ri e^{itR(\cos\theta+i\sin\theta)}}{(Re^{i\theta})^2+\gamma^2} \, d\theta \right| \\ &\le \int_0^\pi \left|\frac{\gamma Ri e^{itR(\cos\theta+i\sin\theta)}}{(Re^{i\theta})^2+\gamma^2} \right|\, d\theta \\ &\le \int_0^{\pi} \frac{R}{R^2-\gamma^2}\,d\theta \\ &\le\frac{\pi R}{R^2-\gamma^2}\xrightarrow{R\to\infty} 0 \end{aligned}

であるから， $\text{(1)}$ 式の両辺 $R\to\infty$ とすることで，

\pi e^{-\gamma t} = \int_{-\infty}^\infty \frac{\gamma e^{ixt}}{x^2+\gamma^2} \, dx.

$t<0$ のときは，半円を下側にとった周回積分を考えれば同様に議論でき，結局，

\pi e^{-\gamma |t|} = \int_{-\infty}^\infty \frac{\gamma e^{ixt}}{x^2+\gamma^2} \, dx

となる。したがって， $E[e^{itX}] = \exp(i x_0 t-\gamma |t|)$ となる。