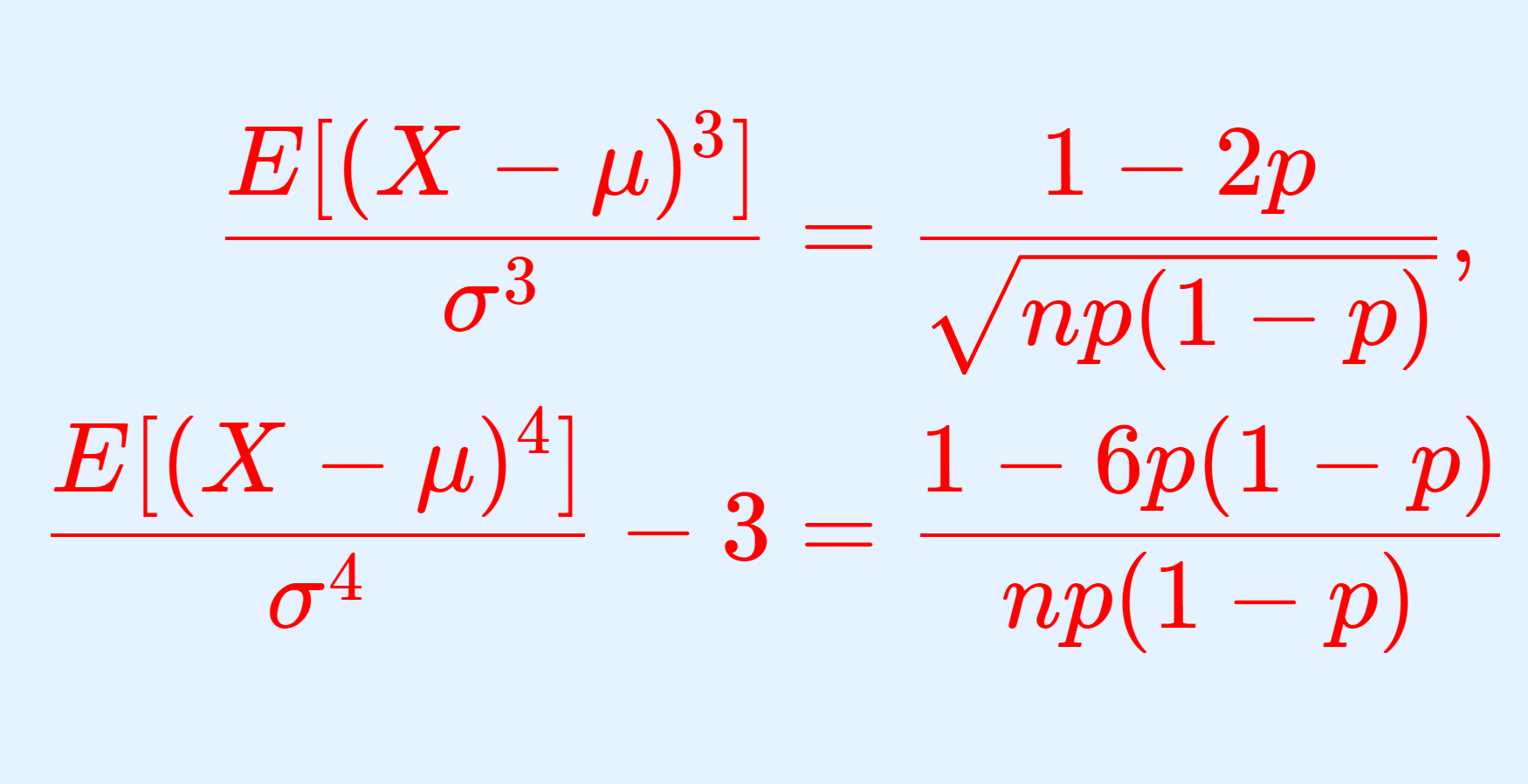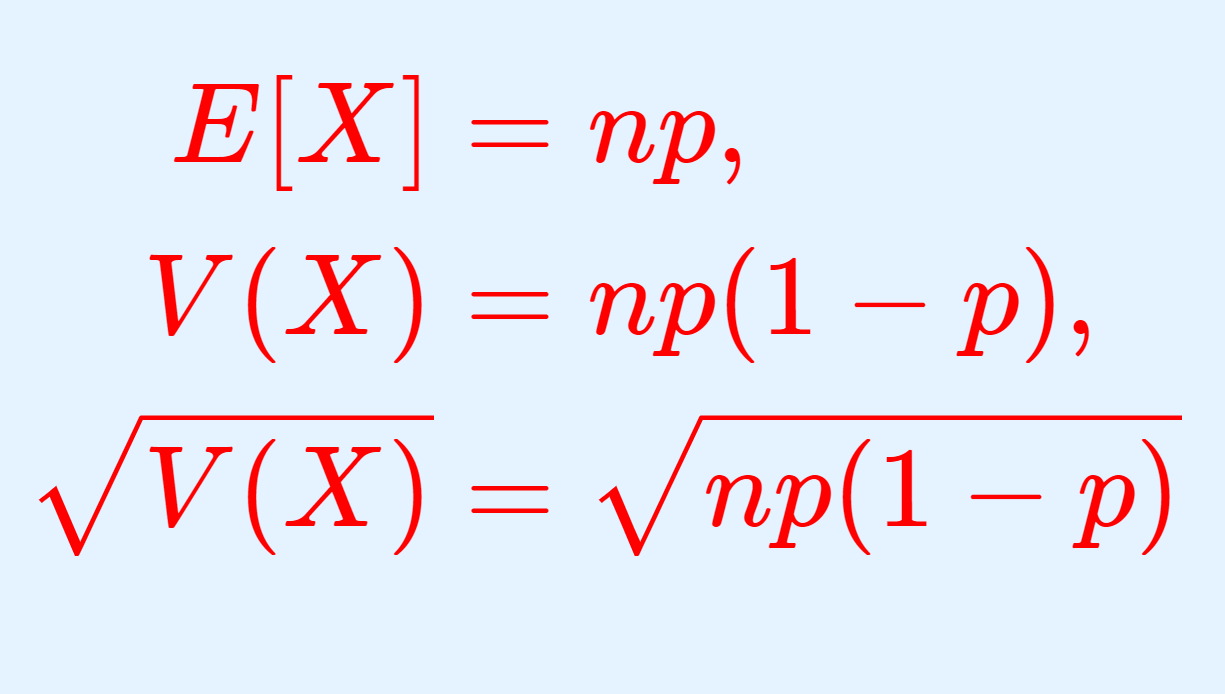二項分布の歪度(わいど)・尖度(せんど)は
\begin{aligned} \frac{E[(X-\mu)^3]}{\sigma^3}&= \frac{1-2p}{\sqrt{np(1-p)}},\\ \frac{E[(X-\mu)^4]}{\sigma^4}-3&= \frac{1-6p(1-p) }{np(1-p)} \end{aligned}となります。これについて,導出の証明を行いましょう。導出のために,二項分布の1~4次モーメントも求めます。
二項分布の歪度・尖度
定理(二項分布の歪度・尖度)
X\sim B(n,p) であるとき, X の歪度・尖度はそれぞれ
\color{red}\begin{aligned} \frac{E[(X-\mu)^3]}{\sigma^3}&= \frac{1-2p}{\sqrt{np(1-p)}},\\ \frac{E[(X-\mu)^4]}{\sigma^4}-3&= \frac{1-6p(1-p) }{np(1-p)} \end{aligned}
となる。ただし, \mu=E[X],\, \sigma=\sqrt{V(X)} (平均・標準偏差)である。
歪度(わいど)とは,分布がどれだけ非対称で歪んで(ゆがんで)いるかを表す指標で,尖度(せんど)とは,正規分布と比べて分布がどれだけ尖って(とがって)いるかを表す指標です。
これの証明について,解説しましょう。
二項分布の歪度・尖度の導出
【準備】二項分布のモーメント
歪度(わいど)・尖度(せんど)の導出に入る前に,二項分布のモーメントを求めましょう。
補題(二項分布のモーメント)
X \sim B(n,p) であるとき,
\small \begin{aligned} E[X]&= np, \\ E[X^2] &= np+n(n-1)p^2, \\ E[X^3] &= np+3n(n-1)p^2+n(n-1)(n-2)p^3, \\ E[X^4] &= np+7n(n-1)p^2+6n(n-1)(n-2)p^3\\ &\quad+n(n-1)(n-2)(n-3)p^4. \end{aligned}これの証明は,特性関数を微分する形で可能です。
補題の証明
二項分布の特性関数は, E[e^{itX}] = (1-p+pe^{it})^n である。この両辺を t で1~4回微分すると,
\small\begin{aligned} E[iXe^{itX}] &= n(1-p+pe^{it})^n ,\\ E[(iX)^2e^{itX}] &=- ne^{it}(1-p+pe^{it})^{n-1}p \\ &\quad-n(n-1)e^{2it} (1-p+pe^{it})^{n-2}p^2 ,\\ \end{aligned} \small \begin{aligned} &E[(iX)^3e^{itX}] \\ &=-ine^{it}(1-p+pe^{it})^{n-1}p \\ &\quad-3in(n-1)e^{2it}(1-p+pe^{it})^{n-2}p^2\\ &\quad-in(n-1)(n-2)e^{3it}(1-p+pe^{it})^{n-3}p^3,\\ &E[(iX)^4e^{itX}] \\ &= ne^{it}(1-p+pe^{it})^{n-1}p \\ &\;+7n(n-1)e^{2it}(1-p+pe^{it})^{n-2}p^2 \\ &\;+6n(n-1)(n-2)e^{3it}(1-p+pe^{it})^{n-3}p^3\\ &\;+n(n-1)(n-2)(n-3)e^{4it}(1-p+pe^{it})^{n-4}p^4. \end{aligned}
これに, t=0 を代入して整理することで,結論を得る。
証明終
各微分の左辺について,期待値の計算と中身の微分を交換していますが,いまの場合,期待値の計算は有限和であるため,簡単に正当化できます。
二項分布の歪度・尖度の導出証明
これと,二項分布の標準偏差
\small\sigma = \sqrt{V(X)} = \sqrt{E[X^2]-E[X]^2} = \sqrt{np(1-p)}
を用いて,歪度(わいど)・尖度(せんど)の証明をしていきましょう。
証明
期待値の線形性より,
\small \begin{aligned}&E[(X-\mu)^3]\\ &=E[X^3]-3\mu E[X^2] + 3\mu^2 E[X]-\mu^3,\\ &E[(X-\mu)^4] \\ &= E[X^4]\!-\!4\mu E[X^3]\! +\!6\mu^2 E[X^2]\! -\! 4\mu^3 E[X]\! +\! \mu^4 \end{aligned}
である。これと,上のモーメントの結果と, \mu = E[X] = np, \, \sigma=\sqrt{np(1-p) } を用いることで,
が計算できる。
証明終
計算は少々大変ですが,無事証明できましたね。