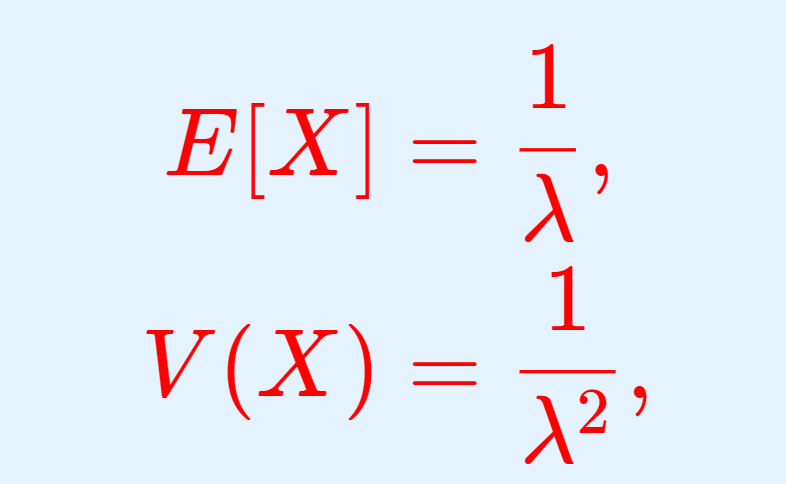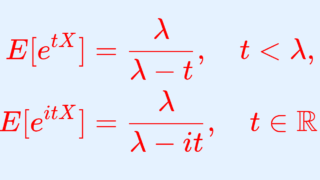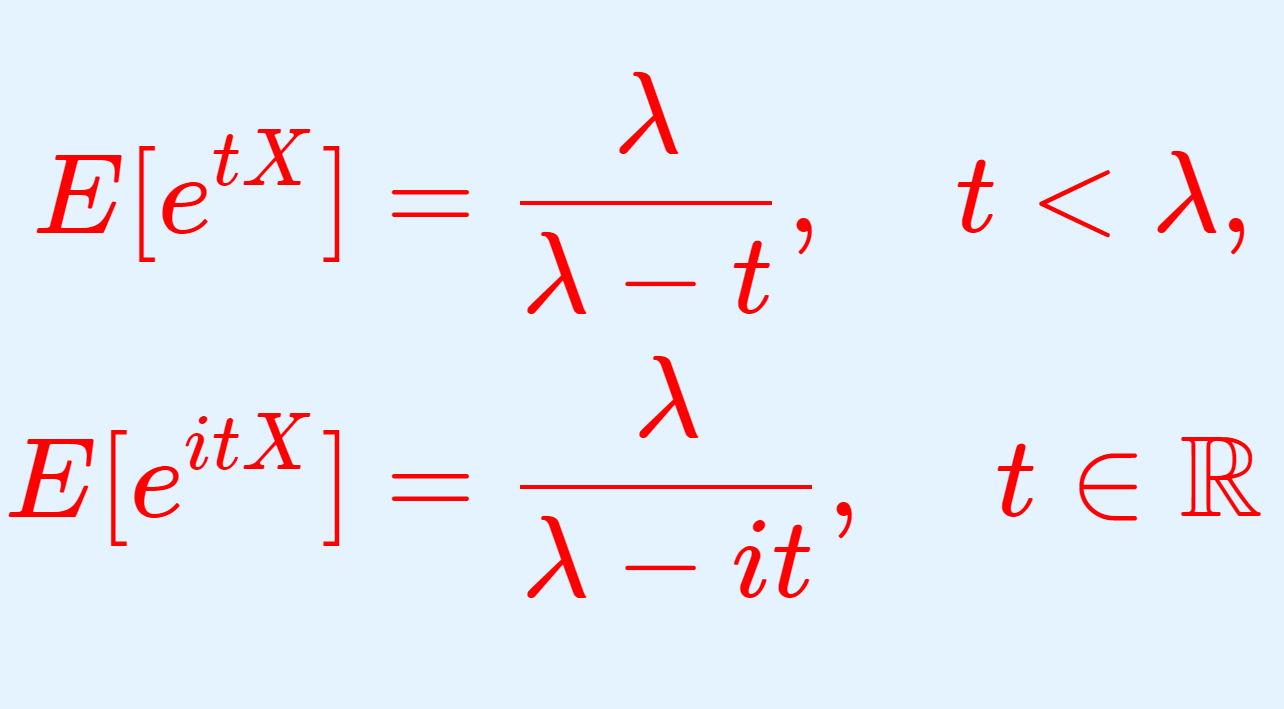PR

指数分布の期待値(平均)・分散・標準偏差とその導出証明

2021.06.18
確率論
大学教養
記事内に広告が含まれています。

指数分布とは，確率密度関数が p(x) = \begin{cases} \lambda e^{-\lambda x } & x\ge 0,\\ 0 & x<0 \end{cases} で表される連続型の確率分布で，その期待値(平均)・分散・標準偏差は，

\begin{aligned} E[X] &= \frac{1}{\lambda}, \\ V(X)&= \frac{1}{\lambda^2 } , \\ \sqrt{V(X)} &= \frac{1}{\lambda} \end{aligned}


となることが知られています。これについて，証明を行いましょう。

指数分布の期待値(平均)・分散・標準偏差

定理（指数分布の期待値(平均)・分散・標準偏差）

\lambda > 0 とおく。 X \sim \operatorname{Exp}(\lambda) とするとき， X の期待値・分散・標準偏差はそれぞれ

\color{red}\begin{aligned} E[X] &= \frac{1}{\lambda}, \\ V(X)&= \frac{1}{\lambda^2 } , \\ \sqrt{V(X)} &= \frac{1}{\lambda} \end{aligned}


である。

期待値と標準偏差がともに 1/\lambda になるわけですね。 \lambda \to 0+ とすると \infty に発散し， \lambda \to\infty とすると， 0 に収束します。

なお，本記事は「指数分布の期待値(平均)・分散・標準偏差の導出」について解説します。指数分布そのものの定義と性質まとめについては，以下の記事を参照してください。

指数分布の定義と例と性質まとめ
指数分布 (exponential distribution) は，確率が指数関数を用いて表現される，「無記憶性」をもつ唯一の連続型確率分布です。これについて，その定義と具体例，性質を図を交えてまとめて紹介しましょう。
mathlandscape.com

指数分布の期待値(平均)の導出証明

指数分布の確率密度関数は，

p(x) = \begin{cases} \lambda e^{-\lambda x } & x\ge 0,\\ 0 & x<0 \end{cases}


であったことを思い出しましょう。これを踏まえて，

  • 指数分布の定義から直接求める方法
  • 特性関数の微分を用いた方法

の２通りで証明していきます。

【期待値(平均)】定義から直接求める方法

まずは，指数分布の定義・期待値(平均)の定義を用いて，素直に計算してみましょう。

証明

期待値の定義から，

\begin{aligned} E[X] &= \int_{-\infty}^\infty xp(x)\, dx =\lambda \int_0^\infty x e^{-\lambda x} \, dx. \end{aligned}


部分積分を用いることで，

\begin{aligned}&\lambda \int_0^\infty x e^{-\lambda x} \, dx \\ &= \left[-xe^{-\lambda x}\right]_0^\infty + \int_0^\infty e^{-\lambda x}\, dx \\ &= 0 + \left[\frac{-1}{\lambda}e^{-\lambda x}\right]_0^\infty \\ &= \frac{1}{\lambda} \end{aligned}


であるから， E[X] = 1/\lambda .

証明終

なお， \lambda x = y で置換積分すると

\begin{aligned}\lambda \int_0^\infty x e^{-\lambda x} \, dx &= \frac{1}{\lambda} \int_0^\infty y e^{-y}\, dy \\ &= \frac{1}{\lambda} \Gamma(2) = \frac{1}{\lambda} 1! = \frac{1}{\lambda} \end{aligned}


とも計算できます。ただし， \Gamma はガンマ関数です。

【期待値(平均)】特性関数の微分を用いて求める方法

次に，特性関数の微分を用いた証明方法を紹介しましょう。まずは，指数分布の特性関数を紹介します。

指数分布の特性関数
E[e^{itX}]=\frac{\lambda}{\lambda-it}, \quad t\in\mathbb{R}.

特性関数の導出については，以下の記事を参照してください。

指数分布の積率母関数・特性関数とその導出証明
指数分布について，それの積率母関数(モーメント母関数)・特性関数について紹介し，それらの導出の証明を行いましょう
mathlandscape.com

証明

特性関数の等式を t で微分すると，

E[iXe^{itX}] = \frac{i\lambda}{(\lambda-it)^2}.


この両辺に t=0 を代入して，

E[iX] = \frac{i}{\lambda}.


すなわち， E[X] = 1/\lambda である。

証明終

なお，今回は「特性関数」を微分しましたが，「積率母関数(モーメント母関数)」を微分しても同様に得ることができます。

指数分布の分散の導出証明

分散は， V(X)=E[X^2] - E[X]^2 の公式を用いて求めることにしましょう。期待値のときと同じく，

  • 指数分布の定義から直接求める方法
  • 特性関数の微分を用いた方法

の２通りで証明していきます。

【分散】定義から直接求める方法

証明

まず，二次モーメントについて，

E[X^2] = \int_{-\infty}^\infty x^2 p(x)\, dx = \lambda \int_0^\infty x^2 e^{-\lambda x}\, dx.


部分積分と，期待値の導出の際にすでに計算した \lambda \int_0^\infty x e^{-\lambda x} \, dx ={1}/{\lambda} を用いると，

\begin{aligned}&\lambda \int_0^\infty x^2 e^{-\lambda x}\, dx \\ &= \left[ -x^2 e^{-\lambda x} \right]_0^\infty + \int_0^\infty 2x e^{-\lambda x} \, dx \\ &= 0 + \frac{2}{\lambda^2} = \frac{2}{\lambda^2} \end{aligned}


であるから， V(X)=E[X^2] - E[X]^2 = \dfrac{2}{\lambda^2} - \dfrac{1}{\lambda^2} = \dfrac{1}{\lambda^2} を得る。

証明終

なお， \lambda x = y で置換積分すると

\begin{aligned}\lambda \int_0^\infty x^2 e^{-\lambda x} \, dx &= \frac{1}{\lambda^2} \int_0^\infty y^2 e^{-y}\, dy \\ &= \frac{1}{\lambda^2} \Gamma(3) = \frac{1}{\lambda^2} 2! = \frac{2}{\lambda^2} \end{aligned}


とも計算できます。ただし， \Gamma はガンマ関数です。

【分散】特性関数の微分を用いて求める方法

さて，分散の方も，特性関数を用いた導出を考えましょう。

証明

特性関数の式 E[e^{itX}]=\dfrac{\lambda}{\lambda-it} の両辺を t で2回微分して

E[(iX)^2e^{itX}] = \frac{-2 \lambda}{(\lambda-it)^3}.


t= 0 を代入すると，

E[(iX)^2 ] = \frac{-2}{\lambda^2}.


であるから， E[X^2] = \dfrac{2}{\lambda^2} . よって， V(X)=E[X^2] - E[X]^2 = \dfrac{2}{\lambda^2} - \dfrac{1}{\lambda^2} = \dfrac{1}{\lambda^2} を得る。

証明終

特性関数の式を用いることで，2次モーメントを求めることができ，分散が計算できましたね。

指数分布の標準偏差について

標準偏差の定義は，分散 V(X) の平方根 \sqrt{V(X)} ですから，分散を上で求めたことで，標準偏差は

\sqrt{V(X)} = \sqrt{\frac{1}{\lambda^2}} = \frac{1}{\lambda}


ですね。

指数分布に関する記事

指数分布の定義と例と性質まとめ
指数分布 (exponential distribution) は，確率が指数関数を用いて表現される，「無記憶性」をもつ唯一の連続型確率分布です。これについて，その定義と具体例，性質を図を交えてまとめて紹介しましょう。
mathlandscape.com