確率変数に対する不等式 P(|X|\ge a) \le \dfrac{E[|X|]}{a} をマルコフの不等式といいます。これについて,分かりやすくかつ厳密に証明しましょう。
マルコフの不等式
定理(マルコフの不等式; Markov’s inequality)
X を確率変数かつ a>0 とする。このとき,
\large\color{red} P(|X|\ge a) \le \dfrac{E[|X|]}{a}
が成立する。
|X| について,ある値より大きい確率を,その期待値をもって上からおさえている定理ですね。
マルコフの不等式の「お気持ち」
マルコフの不等式の「お気持ち」すなわち,感覚的な理解について説明しましょう。 P(|X|\ge a) \le \dfrac{E[|X|]}{a} の代わりに, aP(|X|\ge a)\le E[|X|] を考えます。
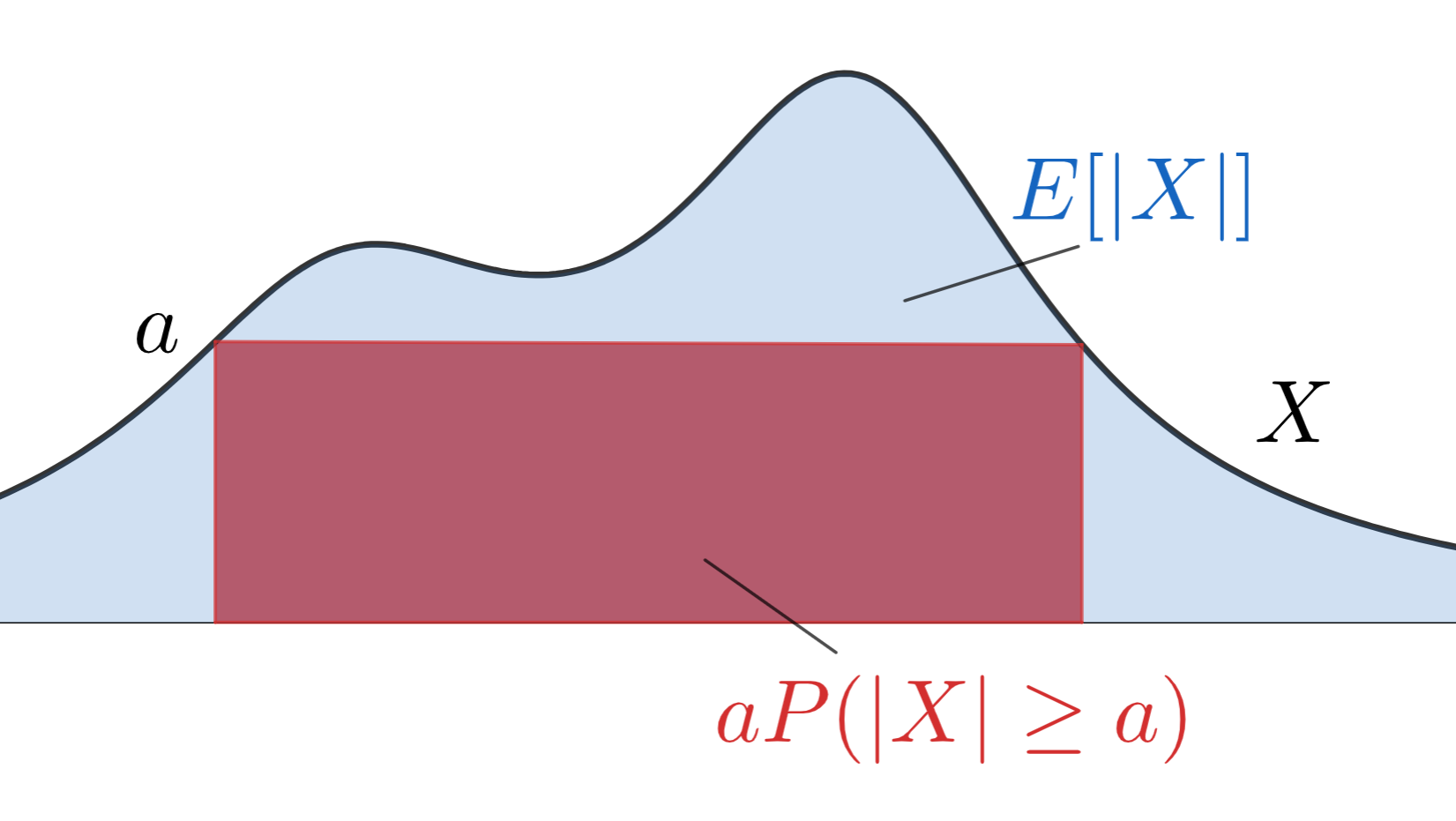
測度論的確率論になじみのない場合は,あまりパッとしないかもしれませんが,確率変数 X というのは,関数の一種です。これを認めて,横軸に各確率の「重み」,縦軸に各重みに対応する関数 X の値をグラフで描いたとしましょう。以下の図では,分かりやすくするために X\ge 0 としています。
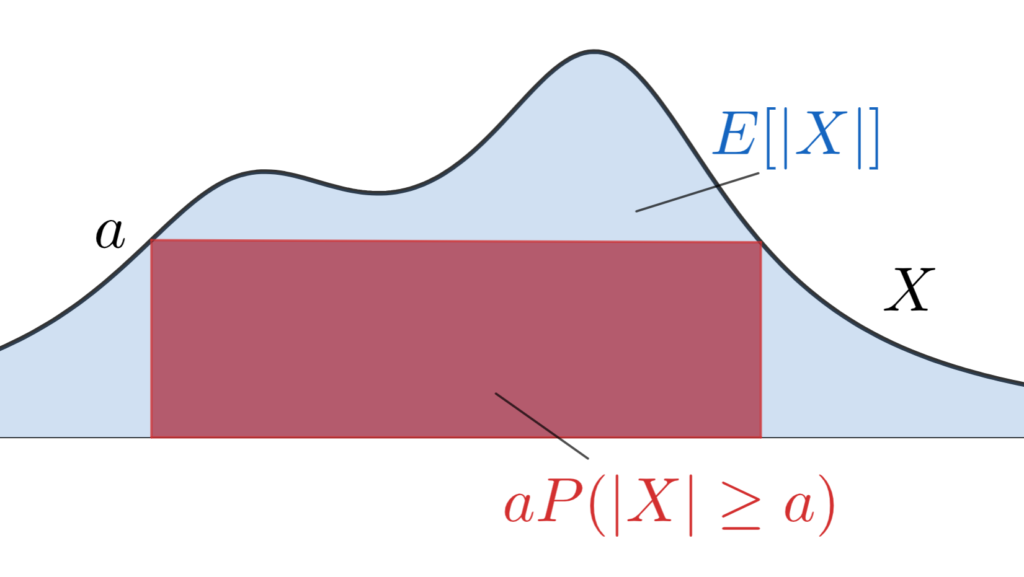
このとき, E[|X|] とは, X のグラフより下の部分,すなわち青色部分の面積を表しています。
一方で, aP(|X|\ge a) とは, |X|\ge a の部分を考えて,その部分のみに a という値を持つグラフの下の部分,すなわち,赤色の長方形の部分の面積を表しています。
マルコフの不等式とは,期待値の表す面積と,その中の長方形の面積の比較をしているわけなんですね。実際には,最後に考えている「一般の測度論におけるマルコフの不等式」を考えた方が分かりやすいかもしれません。
マルコフの不等式の厳密な証明
測度論が分からない場合, X を離散型または連続型の確率変数と思うことにし,離散型の場合は \int_{\infty}^\infty \cdots P(X\in dx) を \sum_{k=-\infty}^\infty \cdots で読み替え,連続型の場合は, \int_{-\infty}^\infty\cdots p(x)\, dx (ただし p(x) は確率密度関数) で読み替えてください。
証明
\begin{aligned} E[|X|] &= \int_{-\infty}^\infty |x| \,P(X\in dx) \\ &\ge \int_{|x|\ge a} |x|\, P(X\in dx) \\ &\ge \int_{|x|\ge a} a \, P(X\in dx) \\ &= a \int_{|x|\ge a} \, P(X\in dx) \\ &= a P(|X|\ge a) \end{aligned}
より,両端辺を a で割って,
証明終
証明は非常に形式的で,シンプルに思うかもしれません。
一般の測度論におけるマルコフの不等式
これまでは,確率測度 P を用いて考えましたが,一般の測度 \mu についても,同様の主張が成り立ちます。 X, P をそれぞれ一般の f, \mu に置き換えて,主張を述べ直しましょう。
定理(マルコフの不等式)
測度 \mu と可測な関数 f に対して, a>0 とすると,
\color{red} \mu(|f|\ge a) \le \frac{1}{a}\int_{-\infty}^\infty |f|\, d\mu
が成り立つ。
\mu は無限測度でも構いません。証明は上と全く同じのため,省略します。
なお, X と f を対応させましたが,測度論的確率論では, X は可測関数であったことに注意しましょう。このように考えると,上の「お気持ち」の説明も分かりやすくなるでしょう。
チェビシェフの不等式
マルコフの不等式を発展させたものに,チェビシェフの不等式があります。これは,以下のようなものです。
定理(チェビシェフの不等式; Chebyshev’s inequality)
X を実数値確率変数とする。このとき, a>0 に対して,
\begin{equation}P(|X|\ge a)\le \frac{E[|X|^2]}{a^2}\end{equation}
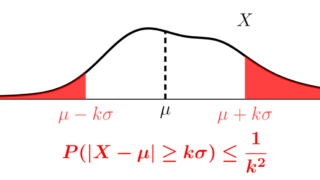
が成り立つ。またこれより, X が有限の期待値 \mu と分散 \sigma^2 をもつとき, k>0 に対して
が成立する。
マルコフの不等式より,こちらの方がよく目にするかもしれません。以下で解説しています。