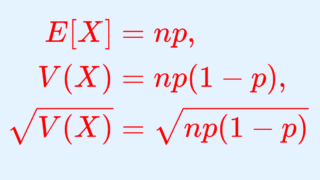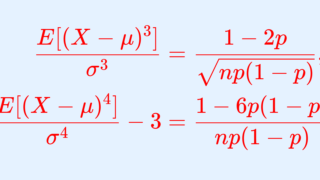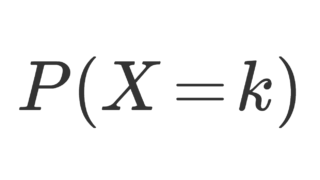二項分布は, n 回コイン投げを行ったときに, k 回表が出る確率を一般化したもので, P(X=k) = {}_n \mathrm{C}_k p^{k}(1-p)^{n-k} となります。そんな二項分布について,その定義と性質を,図解を交えて分かりやすくまとめます。
二項分布の定義
まずは,二項分布の定義と,具体例を確認していきましょう。
二項分布の定義と具体例
定義(二項分布)
0<p<1 ,\,\, n は正の整数とする。 k = 0,1,2,\dots, n に対して,
\color{red} P(X=k) = {}_n \mathrm{C}_k\, p^{k}(1-p)^{n-k}
となるとき,確率変数 X はパラメータ (n,p) に関する二項分布 (binomial distribution) に従うといい, \color{red} X\sim B(n,p) とかく。
二項分布は,確率 p で表が出るコインを n 回投げたときの,表が出る回数をモデル化したものと言えます。

いくつか具体的な値を入れて,そのときの確率がどうなるか考えてみましょう。
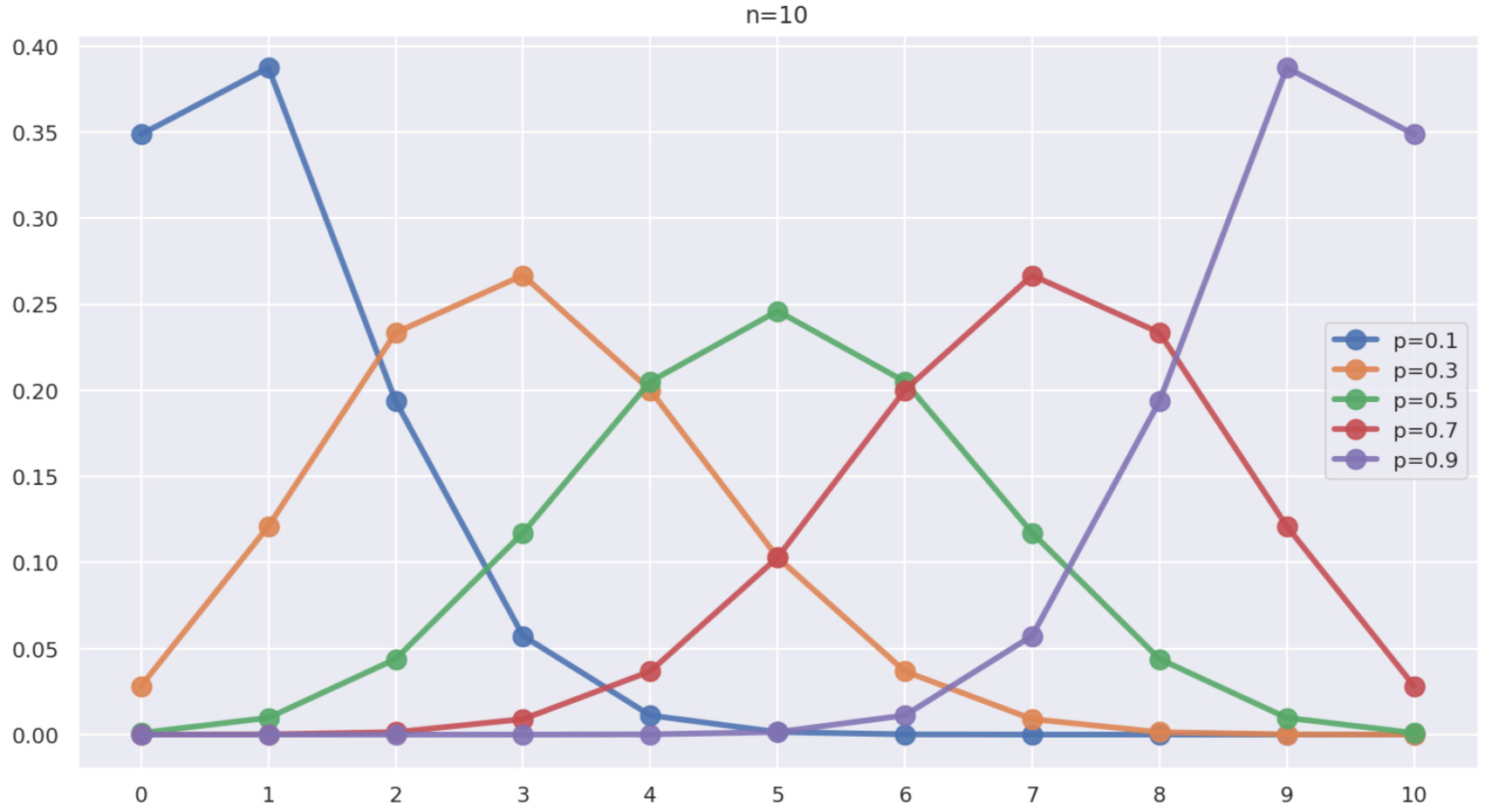
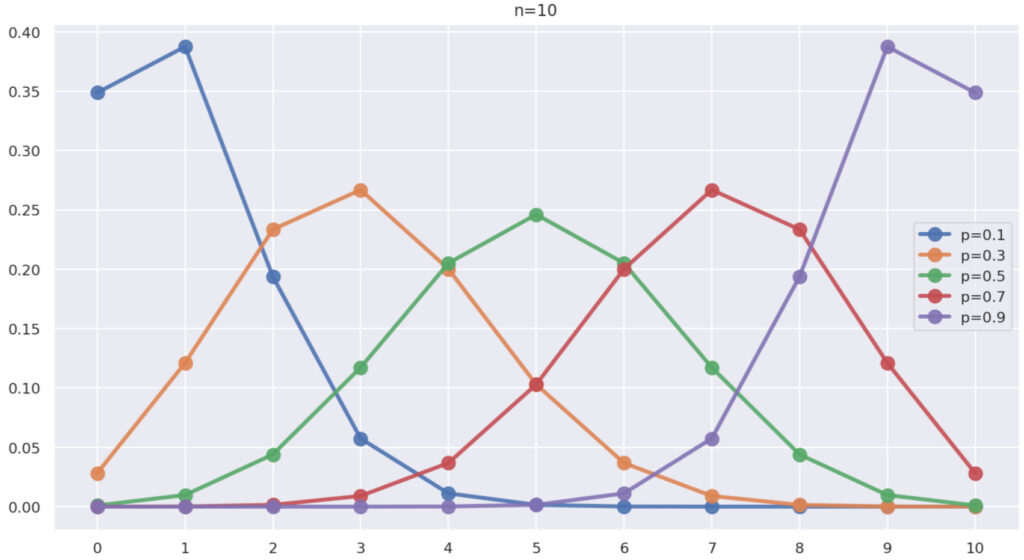
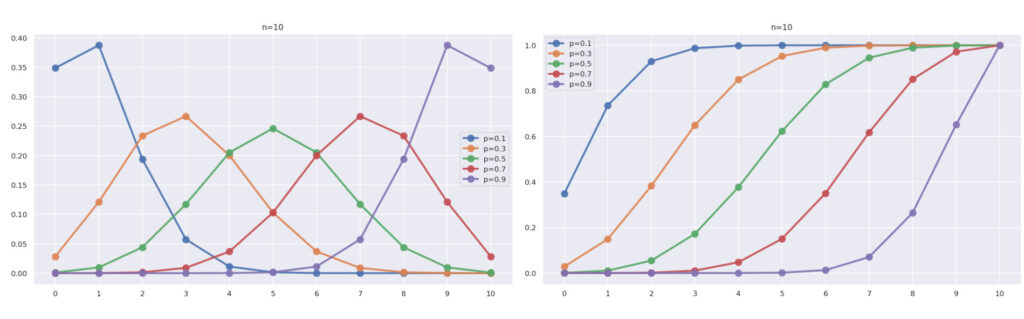
まず,\color{red} n=10 と固定し,\color{red} p=0.1,0.3, 0.5, 0.7, 0.9 と変えたとき,横軸に k \,\,(0\le k \le 10),縦軸に P(X=k) をプロットしたグラフは,以下のようになります。
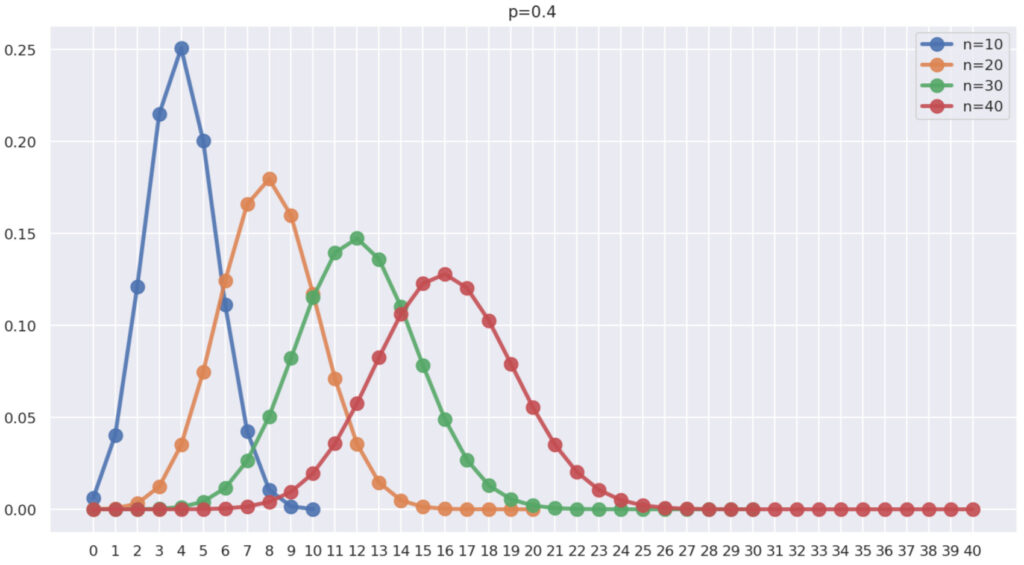
次に, p を固定し, n を変化させてみましょう。 \color{red} p=0.4 とし, \color{red} n=10,20,30,40 と変化させた場合の確率は,以下のようになります。
ベルヌーイ分布との関係
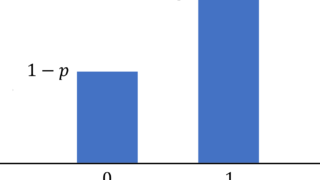
B(n,p) において, n=1 のとき,これは「コインを1回投げただけ」に相当し, \color{red} P(X=1)=p,\, P(X=0) = 1-p となります。これはベルヌーイ分布 (Bernoulli distribution) といいます。これについては,別途以下の記事を参照してください。
また逆に,二項分布は「コインを1回投げる」ということを n 回繰り返すと考えることもできます。よって, X\sim B(n,p) としたとき, P(X_k=1) = p,\, P(X_k=0)=1-p となる互いに独立な n 個のベルヌーイ分布 X_1,X_2,\dots, X_n を用いて,
\color{red} X \stackrel{\mathrm{d}}{=} X_1 + X_2 + \dots + X_n
とかくことができます。 ただし, \stackrel{\mathrm{d}}{=} は「分布の意味で等しい」ことを表します。
ベルヌーイ分布の独立な和が二項分布と言えるわけですね。
二項分布の性質
二項分布の主な性質を列挙します。
| 二項分布 B(n,p) | |
|---|---|
| 確率 P(X=k)\, (k=0,1,\dots,n) | {}_n\mathrm{C}_k\, p^k (1-p)^{n-k} |
| 分布の型 | 離散型 |
| 累積分布関数 F(x) = P(X\le x) | \displaystyle \begin{cases} 0 & x<0 ,\\ \sum_{k=0}^{\lfloor x \rfloor} {}_n\mathrm{C}_k \, p^k (1-p)^{n-k}& 0\le x \le n, \\ 1& n<x.\end{cases} |
| 期待値 \mu=E[X] | np |
| 分散 \sigma^2=V(X) | np(1-p) |
| 標準偏差 \sigma=\sqrt{V(X)} | \sqrt{np(1-p) } |
| 歪度 \frac{E[(X-\mu)^3]}{\sigma^3} | \frac{1-2p}{\sqrt{np(1-p)}} |
| 尖度 \frac{E[(X-\mu)^4]}{\sigma^4} -3 | \frac{1-6p(1-p) }{np(1-p)} |
| 積率母関数 E[e^{tX}] | (1-p+pe^t)^n |
| 特性関数 E[e^{itX}] | (1-p+pe^{it})^n |
| 正規分布による近似(中心極限定理) | p を一定にして n\to\infty とする |
| ポアソン分布による近似(ポアソンの少数の法則) | \lambda =\lim_{n\to\infty} np_n として n\to\infty とする |
累積分布関数以降について,順番に考えていきましょう。
二項分布の累積分布関数(分布関数)
定理(二項分布の累積分布関数)
X\sim B(n,p) であるとき, X の累積分布関数(分布関数)は
\small \color{red}F(x)=\begin{cases} 0 & x<0 ,\\ \sum_{k=0}^{\lfloor x \rfloor} {}_n\mathrm{C}_k \, p^k (1-p)^{n-k}& 0\le x \le n, \\ 1& n<x.\end{cases}
となる。ただし, \lfloor x\rfloor は床関数(ガウス記号)を表す。
これは, F(x) = P(X\le x ) = \sum_{k=0}^{\lfloor x \rfloor} P(X=k) なので,明らかですね。
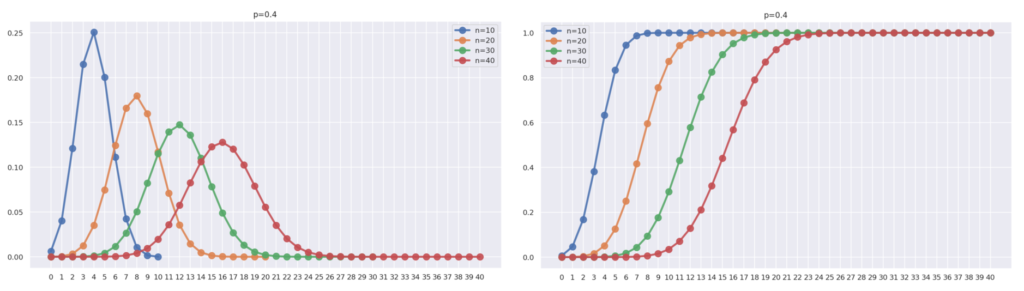
確率(質量)関数と,そのときの累積分布関数を左右に描画すると,以下のようになります。※以下は模式的なものであり,実際の累積分布関数は,床関数(ガウス記号)のグラフのような,不連続なものです。
二項分布の期待値・分散・標準偏差
定理(二項分布の期待値・分散・標準偏差)
X\sim B(n,p) であるとき, X の期待値・分散・標準偏差はそれぞれ
\color{red}\begin{aligned} E[X]&= np, \\ V(X)&= np(1-p), \\ \sqrt{V(X)} &= \sqrt{np(1-p) } \end{aligned}
となる。
これの証明については,以下の記事で行っています。
二項分布の歪度・尖度
定理(二項分布の歪度・尖度)
X\sim B(n,p) であるとき, X の歪度・尖度はそれぞれ
\color{red}\begin{aligned} \frac{E[(X-\mu)^3]}{\sigma^3}&= \frac{1-2p}{\sqrt{np(1-p)}},\\ \frac{E[(X-\mu)^4]}{\sigma^4}-3&= \frac{1-6p(1-p) }{np(1-p)} \end{aligned}
となる。ただし, \mu=E[X],\, \sigma=\sqrt{V(X)} である。
「歪度(わいど)」とは,分布がどれだけ非対称で歪んで(ゆがんで)いるかを表す指標で,「尖度(せんど)」とは,正規分布と比べて分布がどれだけ尖って(とがって)いるかを表す指標です。
これについては,以下の記事で解説しています。
二項分布の積率母関数(モーメント母関数)
定理(二項分布の積率母関数)
X\sim B(n,p) であるとき, X の積率母関数は
\color{red}E[e^{tX}] = (1-p+pe^t)^n
である。
これを証明してみましょう。
証明
\begin{aligned} E[e^{tx} ] &= \sum_{k=0}^n e^{tk} P(X=k) \\ &= \sum_{k=0}^n e^{tk} {}_n\mathrm{C}_k\, p^k (1-p)^{n-k} \\ &= \sum_{k=0}^n {}_n\mathrm{C}_k (pe^{t})^k (1-p)^{n-k} \\ \end{aligned}
であり,二項定理より,
がわかる。
証明終
また,確率変数 X, Y が独立であるとき, \color{red} E[e^{t(X+Y)}] = E[e^{tX}]E[e^{tY}] であることを用いると,以下のような証明も可能です。
別証
X\sim B(n,p) のとき,パラメータ p に従う互いに独立なベルヌーイ分布 X_k \, (1\le k \le n) を用いて,
X\stackrel{\mathrm{d}}{=} X_1 + X_2 + \dots + X_n
とかける( \stackrel{\mathrm{d}}{=} は分布が等しいという意味)。
従って,
\begin{aligned}E[e^{tX}] &= E[e^{t(X_1+\dots+X_n)}] = E[e^{tX_1}]^n \end{aligned}
であり,ベルヌーイ分布の積率母関数は, E[e^{tX_1}]= 1-p+pe^t である(→ベルヌーイ分布とは~定義と性質の導出~)から,
がわかる。
別証終
二項分布の特性関数
定理(二項分布の特性関数)
X\sim B(n,p) であるとき, X の特性関数は
\color{red}E[e^{itX}] = (1-p+pe^{it})^n
である。
これの証明は,積率母関数のときとほぼ同じですが,一応確認してみましょう。
証明
\begin{aligned} E[e^{itx} ] &= \sum_{k=0}^n e^{itk} P(X=k) \\ &= \sum_{k=0}^n e^{itk} {}_n\mathrm{C}_k\, p^k (1-p)^{n-k} \\ &= \sum_{k=0}^n {}_n\mathrm{C}_k (pe^{it})^k (1-p)^{n-k} \\ \end{aligned}
であり,二項定理より,
がわかる。
証明終
また,確率変数 X, Y が独立であるとき, \color{red} E[e^{it(X+Y)}] = E[e^{itX}]E[e^{itY}] であることを用いると,積率母関数のときと同様に,以下のような証明も可能です。
別証
X\sim B(n,p) のとき,パラメータ p に従う互いに独立なベルヌーイ分布 X_k \, (1\le k \le n) を用いて,
X\stackrel{\mathrm{d}}{=} X_1 + X_2 + \dots + X_n
とかける( \stackrel{\mathrm{d}}{=} は分布が等しいという意味)。
従って,
\begin{aligned}E[e^{itX}] &= E[e^{it(X_1+\dots+X_n)}] = E[e^{itX_1}]^n \end{aligned}
であり,ベルヌーイ分布の特性関数は, E[e^{itX_1}]= 1-p+pe^{it} である(→ベルヌーイ分布とは~定義と性質の導出~)から,
がわかる。
別証終
二項分布の正規分布による近似
np, np(1-p) が十分大きいとき,二項分布 B(n,p) は,正規分布 N(np, np(1-p)) で近似できます。
以下は, p=0.4, \,n=50 のときに二項分布のグラフ(青)と該当する正規分布のグラフ(赤)を重ねたものです。
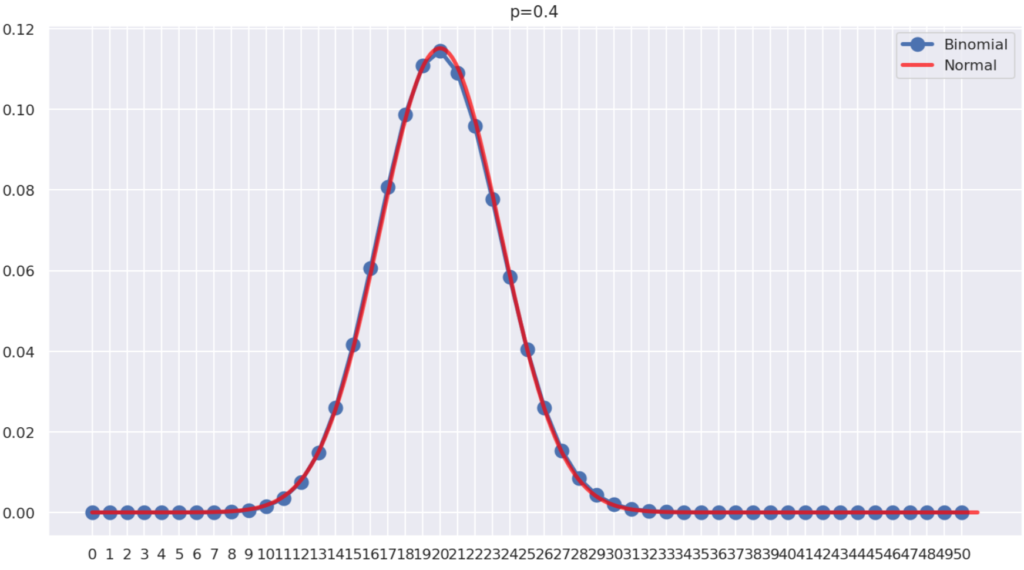
良好に近似できていることが分かりますね。
厳密には,中心極限定理の話になります。
二項分布のポアソン分布による近似
以下の定理が知られています。
定理(ポアソンの少数の法則)
\lambda>0 とし, X_n \sim B(n, p_n ) とする。ただし, \{p_n\} は \lim_{n\to\infty}np_n = \lambda をみたす (0, 1 ) 値の数列である。
このとき, X_n はパラメータ \lambda をもつポアソン分布に分布収束する。すなわち, l=0,1,2,\dots に対し,
\color{red} \lim_{n\to\infty}P(X_n =l) = e^{-\lambda} \frac{\lambda^l}{l!}.ラフに言うと, n が十分大きく, p_n が十分小さいとき,ポアソン分布で近似できるということですね。