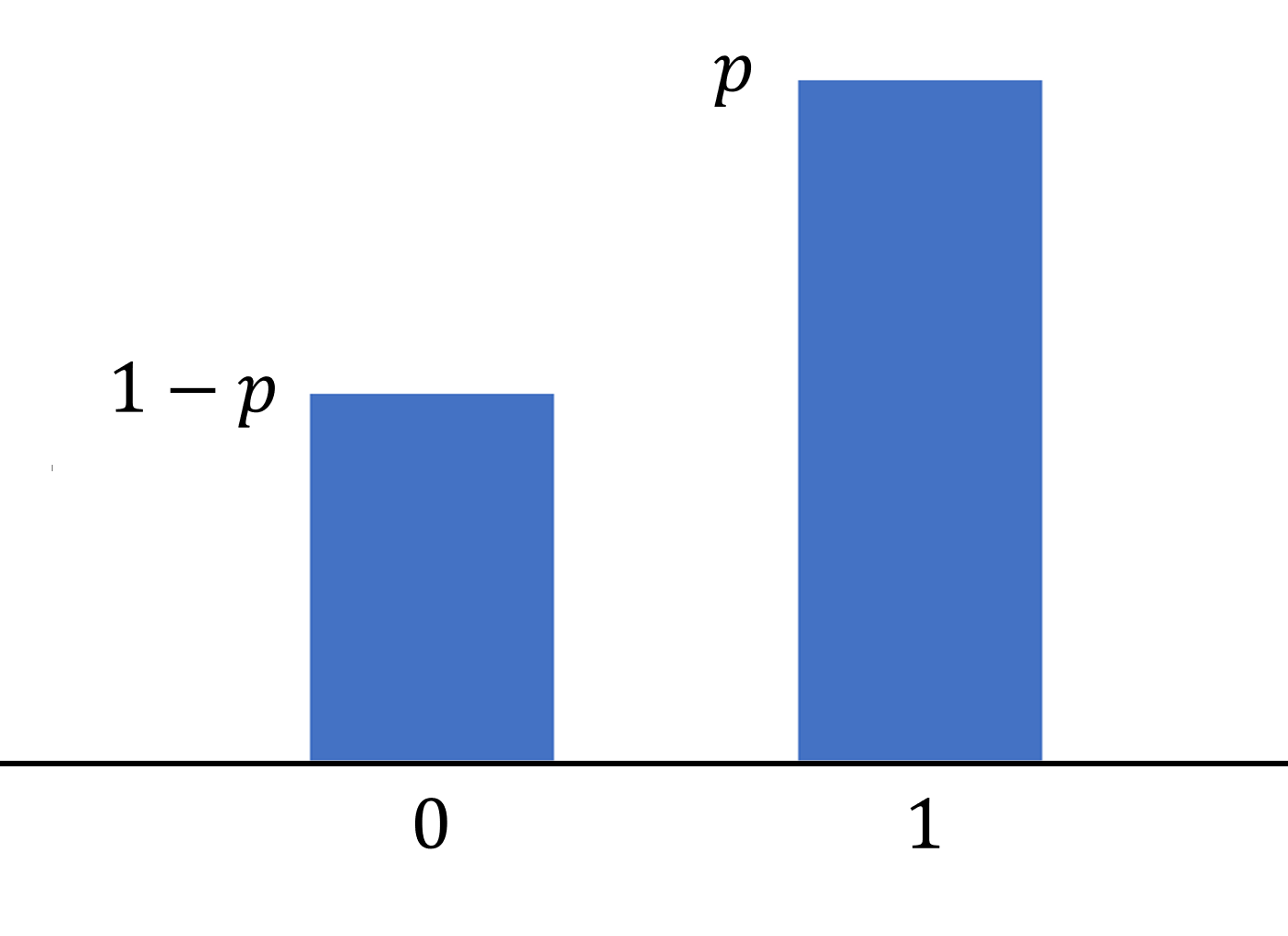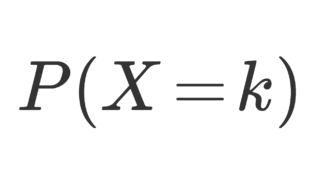ベルヌーイ分布は,ある確率 p で 1 を,残りの確率 1-p で 0 となるような確率分布のことです。これについて,その定義と性質を述べましょう。
ベルヌーイ分布の定義
定義(ベルヌーイ分布)
0<p<1 とする。確率変数 X がベルヌーイ分布 (Bernoulli distribution) に従うとは,
\color{red} P(X=1) = p, \quad P(X=0)=1-p
となることである。
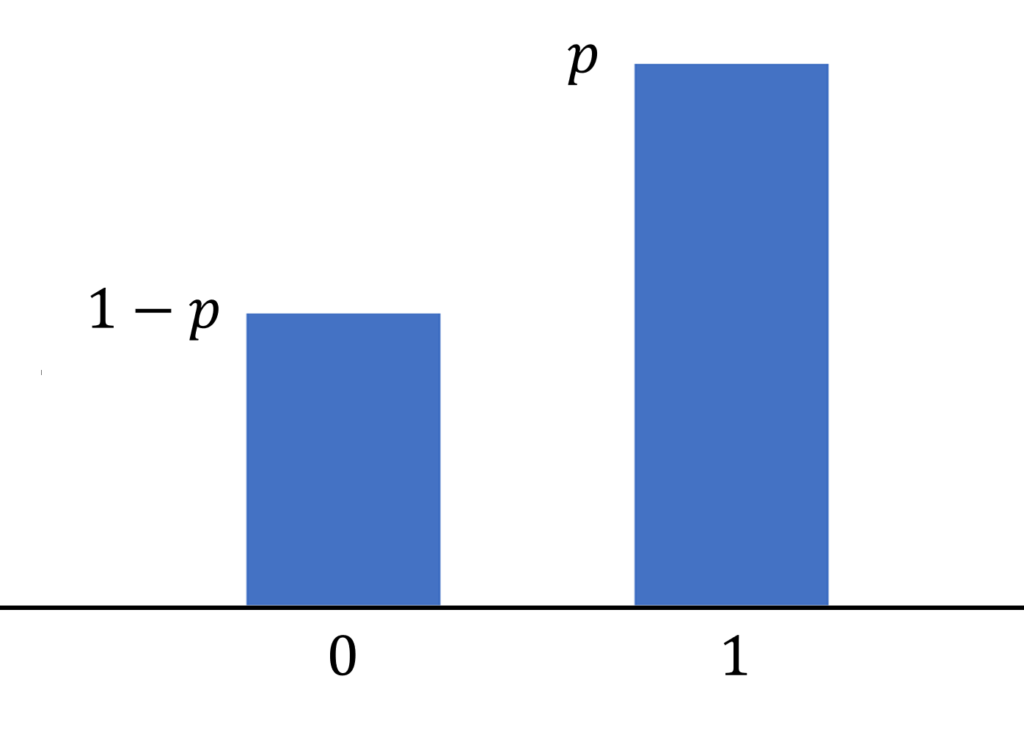
単純な分布ですね。
もっとも基本的な例が,コイン投げでしょう。ある確率 p で表が出て,残りの確率 1-p で裏が出るようなコインを考えます。
表が出れば X=1 ,裏が出れば X=0 となるように,確率変数 X を定めると, X はベルヌーイ分布に従っていると言えますね。 p = 1/2 とすると,これは平等なコインなわけです。

なお,ベルヌーイ分布の定義は, k=0,1 でまとめて
\color{red} P(X=k) = p^k (1-p)^{1-k} \quad (k=0,1)
と書くことも可能です。
ベルヌーイ分布の諸性質
まずは,ベルヌーイ分布の基本的な性質を列挙しましょう。
| ベルヌーイ分布 | |
|---|---|
| 確率 | P(X=1)=p, \,\, P(X=0)=1-p |
| 分布の型 | 離散型 |
| 累積分布関数 F(x) = P(X\le x ) | \begin{cases} 0& x < 0, \\ 1-p & 0 \le x < 1, \\ 1 & 1\le x \end{cases} |
| 平均(期待値) E[X] | p |
| 分散 V(X) | p(1-p) |
| 標準偏差 \sqrt{V(X)} | \sqrt{p(1-p) } |
| 積率母関数 E[e^{tX}] | 1-p+ pe^t |
| 特性関数 E[e^{itX}] | 1-p+pe^{it} |
累積分布関数以降について,確認していきましょう。
ベルヌーイ分布の累積分布関数
ベルヌーイ分布の累積分布関数(分布関数)は,
F(x) = P(X\le x) = \begin{cases} 0& x < 0, \\ 1-p & 0 \le x < 1, \\ 1 & 1\le x \end{cases}
になります。グラフを描くと,以下のようになります。
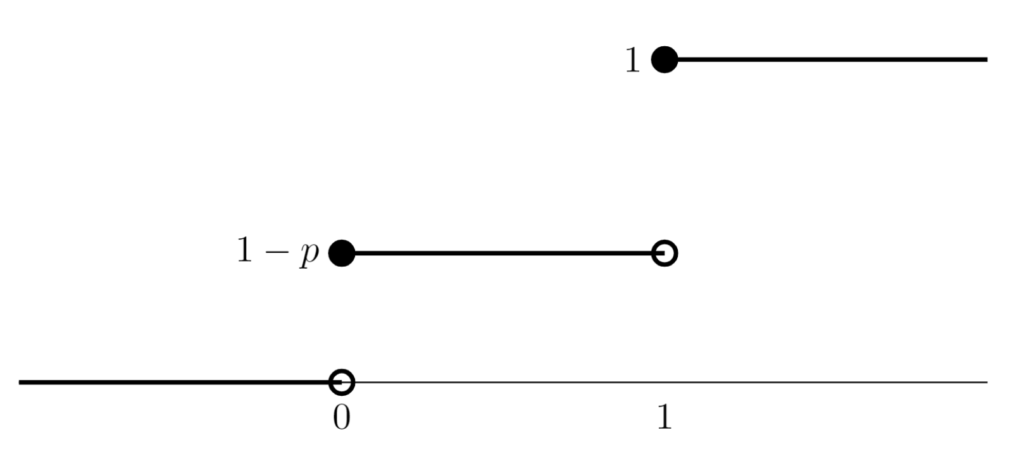
ベルヌーイ分布の平均(期待値)
ベルヌーイ分布の平均(期待値)は,
E[X] = 1\cdot P(X=1) + 0 \cdot P(X=0) = p
と計算できます。
ベルヌーイ分布の分散
ベルヌーイ分布の分散は,平均が p であることから,
\begin{aligned} V(X) &= E[|X-p|^2] \\&= |1-p|^2 P(X=1) + |0-p|^2 P(X=0) \\ &= p(1-p)^2 + p^2(1-p) = p(1-p)\end{aligned}
と計算できますね。
ベルヌーイ分布の標準偏差
標準偏差は,分散のルート \sqrt{V(X)} ですから,
\sqrt{V(X)} = \sqrt{p(1-p) }
となります。
ベルヌーイ分布の積率母関数(モーメント母関数)
ベルヌーイ分布の積率母関数(モーメント母関数)については,
\begin{aligned}E[e^{tX}] &= e^t P(X=1) + e^0 P(X=0)\\ &= pe^t + 1-p \end{aligned}
なので,求められましたね。
ベルヌーイ分布の特性関数
ベルヌーイ分布の特性関数は,
\begin{aligned}E[e^{itX}] &= e^{it} P(X=1) + e^0 P(X=0)\\ &= pe^{it} + 1-p \end{aligned}
なので,得られましたね。