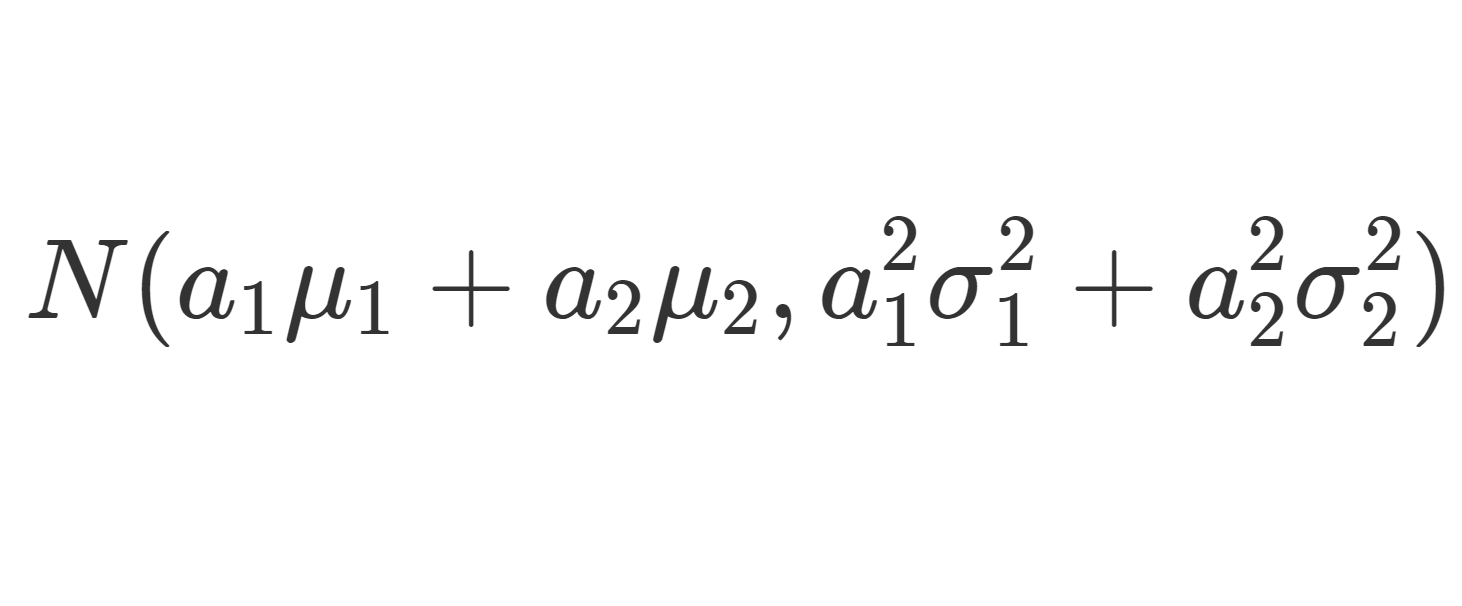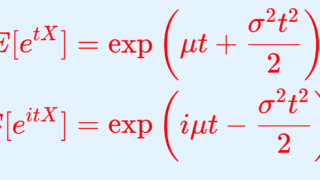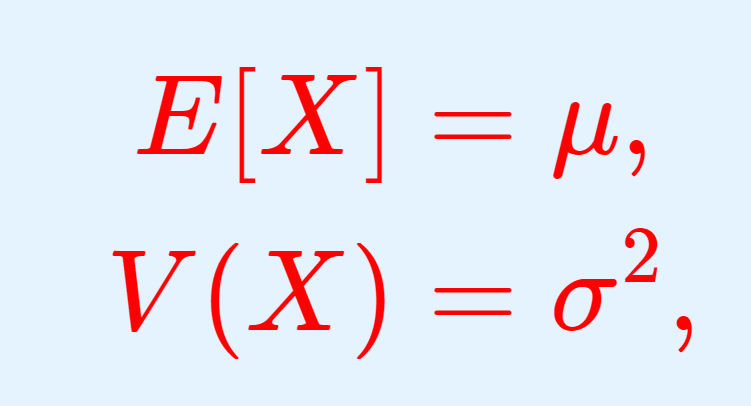X_1\sim N(\mu_1, \sigma_1^2), \, X_2\sim N(\mu_2, \sigma_2^2) とするとき, a_1X_1+a_2X_2\sim N(a_1\mu_1+a_2\mu_2, a_1^2\sigma_1^2+a_2^2\sigma_2^2) となることが知られています。これを,正規分布の再生性といいます。これについて「和の再生性」と「定数倍の再生性」に分けて証明しましょう。
正規分布の再生性
定理(正規分布の再生性)
\mu_1, \mu_2 \in \mathbb{R},\; \sigma_1,\sigma_2>0 とする。 X_1 \sim N(\mu_1, \sigma_1^2),\; X_2\sim N(\mu_2, \sigma_2^2) を独立とすると, a_1, a_2\in \mathbb{R} に対し,
\small\color{red} a_1X_1+a_2X_2\sim N(a_1\mu_1+a_2\mu_2, a_1^2\sigma_1^2+a_2^2\sigma_2^2)
である。特に,正規分布の和や定数倍は,また正規分布になる。
同じ分布族の独立な確率変数を2つ足すと,また同じ分布族に属するとき,これを分布の再生性 (reproductive property) といいます。正規分布やポアソン分布は,再生性をもつ分布として有名です。
証明に入る前に,まずは,正規分布の定義を軽くおさらいしておきましょう。
X を確率変数, \mu\in \mathbb{R},\; \sigma > 0 とする。 X の確率密度関数が
\color{red} p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
となるとき, X は平均 \mu ,分散 \sigma^2 の正規分布 (normal distribution) に従うといい, \color{red} X\sim N(\mu, \sigma^2) とかく。
正規分布のさまざまなまとめについては,以下の記事を参照してください。
これをもとに,再生性の証明をしていきます。
正規分布の再生性の証明
再生性の証明は,
\begin{gathered} X_1+X_2 \sim N(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2), \\ aX \sim N(a\mu, a^2\sigma^2) \end{gathered}
すなわち,「和の再生性」と「定数倍の再生性」に分けて考えることができます。この2つが証明できれば,「定数倍の再生性」を用いてから,「和の再生性」を用いることで,
が証明できますね。では,やっていきましょう。
正規分布の和の再生性の証明
さて,まずは和の再生性 X_1+X_2 \sim N(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2) の証明をしましょう。
- 特性関数を用いた証明
- 確率密度関数を用いた証明
の両方を考えましょう。
【和の再生性】特性関数を用いた証明
特性関数を用いて証明する前に,正規分布の特性関数について述べておきます。
これの証明については,以下を参照してください。
上と,確率変数 X_1, X_2 が独立のとき, E[e^{it(X_1+X_2)}]=E[e^{itX_1}]E[e^{itX_2}] となることを用いて進めましょう。
証明
X_1 \sim N(\mu_1, \sigma_1^2),\; X_2\sim N(\mu_2, \sigma_2^2) を独立とすると,
\begin{aligned} &E[e^{it(X_1+X_2)}]\\ &= E[e^{itX_1}]E[e^{itX_2}] \\ &= {E[e^{itX_1}]} {E[e^{itX_2}]}\\ &={\left\{\exp \left( i\mu_1 t - \frac{\sigma_1^2 }{2}t^2 \right)\right\}} \\ &\quad\times {\left\{ \exp \left( i\mu_2 t - \frac{\sigma_2^2 }{2}t^2 \right) \right\}} \\ &= \exp\left( i(\mu_1+\mu_2)t + \frac{\sigma_1^2+\sigma_2^2}{2}t^2\right) \end{aligned}
である。これは,正規分布 N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2) の特性関数に一致しており,特性関数と分布は一対一に対応しているから,
である。
証明終
【和の再生性】確率密度関数を用いた証明
一般に,独立な2つの確率変数 X_1,X_2 の確率密度関数を p_1(x), p_2(x) とすると,その和 X_1+X_2 の確率密度関数 p(x) は,その畳み込み (convolution) p_1*p_2 (x),すなわち,
\begin{aligned} p(x) &= p_1*p_2(x)\\ &= \int_{-\infty}^\infty p_1(x-y)p_2(y)\, dy \end{aligned}
となることを用います。
証明
X_1 \sim N(\mu_1, \sigma_1^2),\; X_2\sim N(\mu_2, \sigma_2^2) を独立とし,それぞれの確率密度関数を p_1(x), p_2(x) とする。このとき,和 X_1+X_2 の確率密度関数 p(x) は,両者の畳み込み
\begin{aligned} p(x) &= p_1*p_2(x)\\ &= \int_{-\infty}^\infty p_1(x-y)p_2(y)\, dy \end{aligned}
でかけることを用いる。
であり,最終項の指数部分について,
ただし, C = \dfrac{x\sigma_2^2+\mu_1\sigma_2^2-\mu_2\sigma_1^2}{\sigma_1^2+\sigma_2^2}である。ここで,ガウス積分により,
であるから,和の確率密度関数について,
となる。これは, N(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2) の確率密度関数である。よって,
証明終
正規分布の定数倍の再生性の証明
続いて,定数倍の再生性 aX \sim N(a\mu, a^2\sigma^2) を証明しましょう。証明は,再び2通りで行いましょう。
【定数倍の再生性】特性関数を用いた証明
証明
\begin{aligned} E[e^{it(aX)}] &= E[e^{i(at)X}] \\ &=\exp \left( i\mu at - \frac{\sigma^2}{2}(at)^2 \right) \\ &= \exp \left( i a\mu t - \frac{a^2\sigma^2}{2}t^2 \right) \end{aligned}
であり,これは N(a\mu, a^2\sigma^2 ) の特性関数に一致しており,分布と特性関数は一対一に対応しているから,
証明終
【定数倍の再生性】確率密度関数を用いた証明
証明
s<t, \; a\in \mathbb{R}\setminus\{0\} とする。
\begin{aligned} P(aX \in [s,t]) &= P(X \in [s/a, t/a]) \\ &=\int_{s/a}^{t/a} p(x)\, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{s/a}^{t/a} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx \end{aligned}
ここで, y=ax で置換積分すると,
であるから, aX の確率密度関数は \frac{1}{\sqrt{2\pi a^2\sigma^2}} e^{-\frac{(y-a\mu)^2}{2 a^2\sigma^2}} となる。これは, N(a\mu, a^2\sigma^2) の確率密度関数と一致しているので,
である。
証明終