ビュフォンの針とは,針を落として,等間隔に並んだ線と交わる確率を求めるという話です。円が全く絡んでいないにもかかわらず,確率に円周率 \pi が出てくるため,不思議に思われることが多いです。
ビュフォンの針について,その確率を数学的に導出しましょう。
ビュフォンの針
定理(ビュフォンの針: Buffon’s needle)
下図のように,長さ l の針を間隔 d の線に落とすと,針が線と交差する確率は
\small \color{red}\!\!\!\! \!\!\! \begin{dcases} \boldsymbol{\frac{2l}{\pi d}} & \text{if } l\le d, \\ \boldsymbol{ 1\! -\! \frac{2l}{\pi d}\left( \frac{d}{l}\sin^{-1}\frac{d}{l}\! +\!\sqrt{1\! - \! \frac{d^2}{l^2}}\! -\! 1\right)} & \text{if }d< l\end{dcases}
となる。

たとえば上の図の場合,針7本のうち,線と交差しているのは4本ですね。このように,線と針は交差する場合と交差しない場合がありますが,その確率は上のように書けるというわけです。
さて,ここで針は線の上に無作為に落とします。無作為とは,針の位置・角度がそれぞれ一様分布に従っているということです。
針の角度と,線と平行な向きの反時計回りに測った角度を 0\le \theta \le \pi としましょう。このとき以下の図から,線と交わる確率 p(\theta) は \color{red}p(\theta)=\min\left\{ \dfrac{l\sin\theta}{d}, 1\right\} ,すなわち, \dfrac{l\sin\theta}{d} と 1 の小さい方だと分かります。
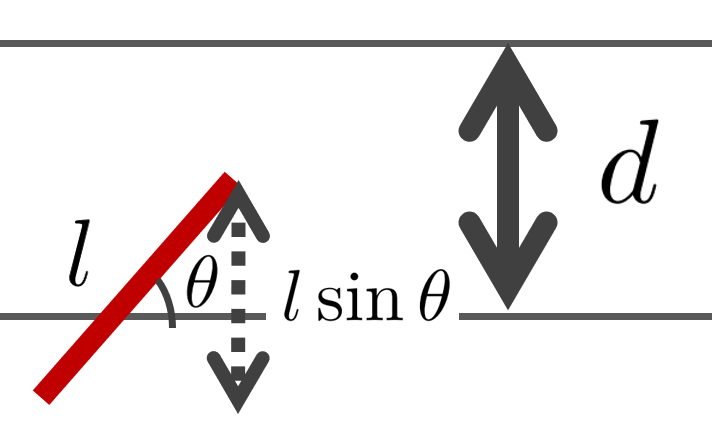
実際の針は,角度が 0\le \theta\le \pi の範囲を動きますから, p(\theta) をこの範囲で積分して,全体の面積 \int_0^\pi 1\, dx=\pi で割り算してあげればよいというわけです。
ビュフォンの針の証明
上の図を踏まえて,証明していきます。求める確率は,以下の図における灰色全体(うすい灰色+濃い灰色)の面積における,濃い灰色の面積の割合です。
証明
l\le d のとき
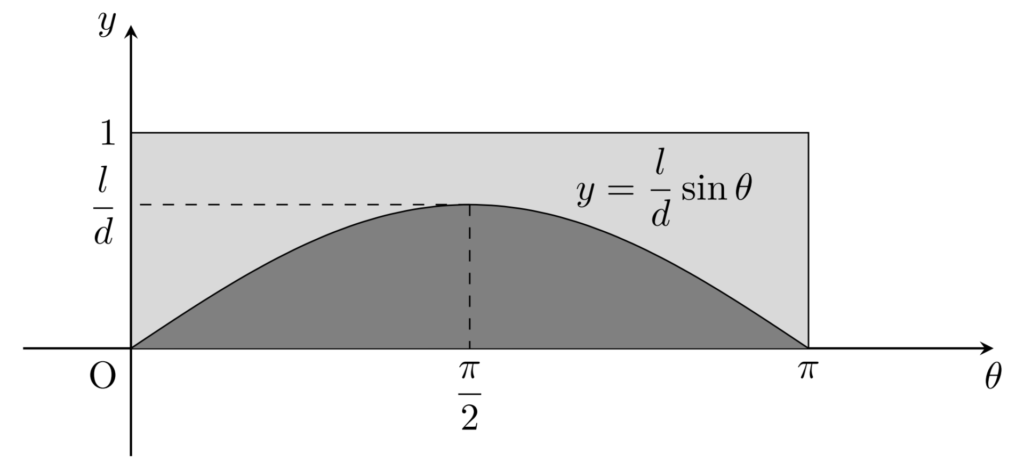
うすい灰色全体の面積は \pi なのに対して,濃い灰色の部分の面積は
\int_0^\pi \frac{l}{d} \sin \theta\, \mathrm{d}\theta = \left[-\frac{l}{d}\cos\theta\right]_0^\pi =\frac{2l}{d}
であるから,灰色全体に対して,濃い灰色の部分の割合は, \dfrac{2l}{\pi d} である。
d< l のとき
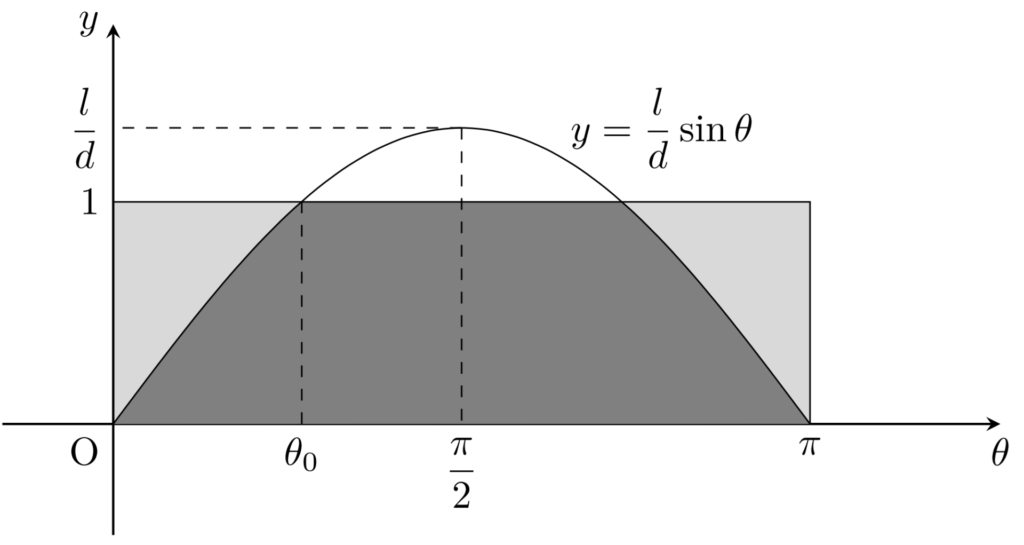
\theta_0=\sin^{-1} \dfrac{d}{l} と定める。すなわち, 0\le \theta_0\le \pi/2 を \sin \theta_0=d/l をみたすものとして定める。
このとき,濃い灰色の面積について, \theta=\pi/2 に関する対称性を利用すると,
\begin{aligned}&2\left\{\int_0^{\theta_0}\frac{l}{d}\sin \theta \mathrm{d}\theta + \left(\frac{\pi}{2}-\theta_0\right)\right\} \\ &= \left[ -\frac{2l}{d}\cos\theta\right]_0^{\theta_0} +2 \left(\frac{\pi}{2}-\theta_0\right) \\ &= \frac{2l}{d} (1-\cos\theta_0) +\pi -2\theta_0 \end{aligned}
ここで, \cos\theta_0=\sqrt{1-\sin^2\theta_0}= \sqrt{1-\dfrac{d^2}{l^2}} も踏まえると,
なので,灰色全体に対して濃い灰色の割合は
である。
証明終
ビュフォンの針を用いた円周率の近似
簡単のため, l=d としましょう。すなわち,針の長さが線の間隔と等しいとします。すると,針を落としたときに線の交わる確率は \dfrac{2}{\pi} になります。
実際に針を N 本落として, M 本が線と交わったとしましょう。このとき,おおよそ
\frac{M}{N}\approx \frac{2}{\pi}
すなわち
と近似できるわけです。この手法を用いれば,円周率 \pi を求めることができそうですね。実際のところは,この近似手法は近似の精度が良くない(精度よく近似するためには,ものすごい数の針を投げなければならない)ため,使われることは少ないです。