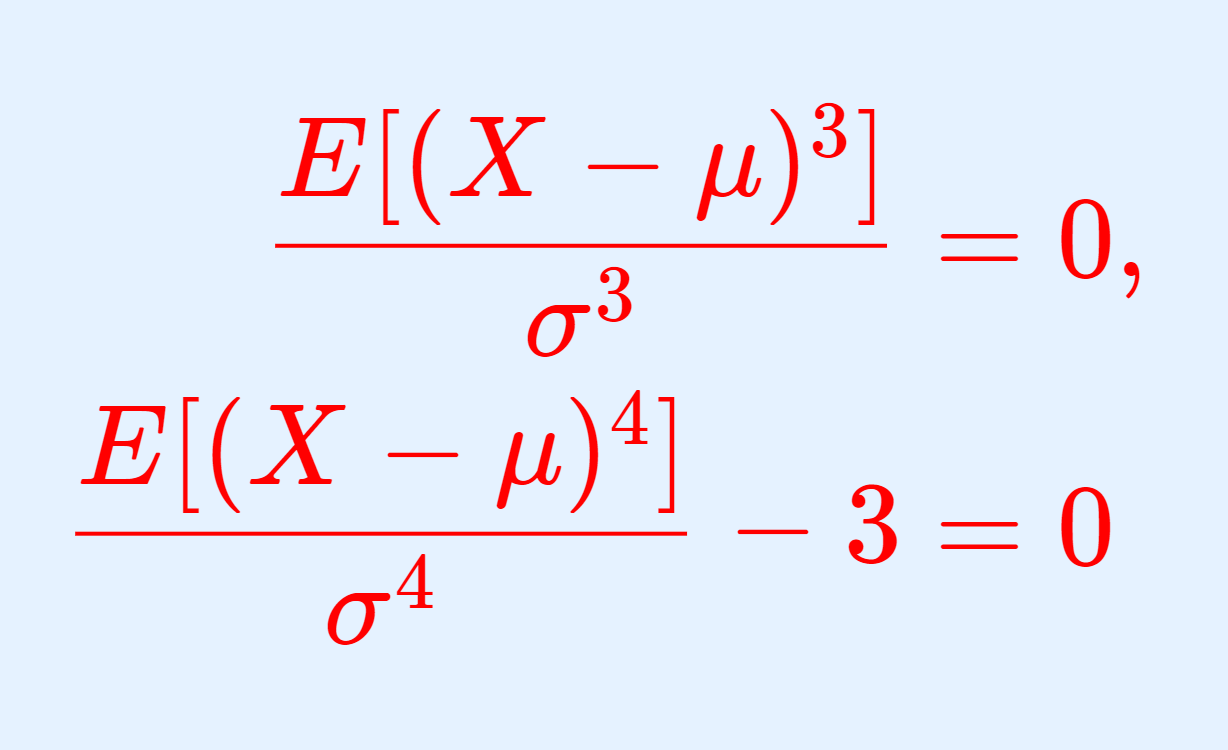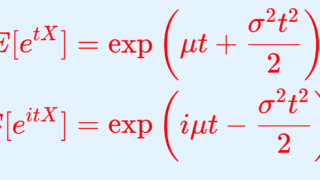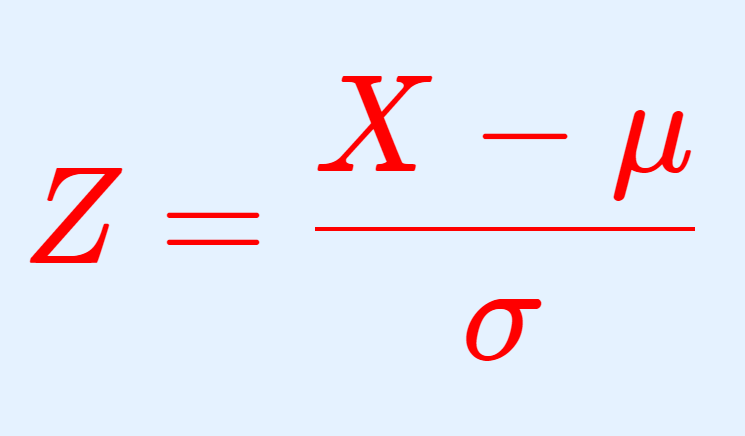正規分布の歪度・尖度とその導出証明

正規分布の歪度(わいど)・尖度(せんど)について，

\begin{aligned} \dfrac{E[(X-\mu)^3]}{\sigma^3}&= 0, \\ \dfrac{E[(X-\mu)^4]}{\sigma^4} -3&= 0 \\ \end{aligned}

と，どちらも $0$ になることが知られています。これについて，その導出の証明を行いましょう。

正規分布の歪度・尖度
正規分布の歪度・尖度の導出証明
1. 正規分布の歪度の導出
  1. 確率密度関数を用いる方法
  2. 特性関数の微分を用いる方法
2. 正規分布の尖度の導出
  1. 特性関数の微分を用いる方法
正規分布に関する記事

正規分布の歪度・尖度

定理（正規分布の歪度・尖度）

$X\sim N(\mu,\sigma^2 )$ とする。このとき， $X$ の歪度・尖度はそれぞれ

\color{red} \begin{aligned} \dfrac{E[(X-\mu)^3]}{\sigma^3}&= 0, \\ \dfrac{E[(X-\mu)^4]}{\sigma^4} -3&= 0 \\ \end{aligned}

である。

歪度（わいど）とは，分布がどれだけ非対称で歪んで（ゆがんで）いるかを表す指標で，尖度（せんど）とは，「正規分布と比べて」分布がどれだけ尖って（とがって）いるかを表す指標です。正規分布は，ちょうどどちらも $0$ になります。

最初に，正規分布の確率密度関数を確認しておきましょう。

正規分布の定義

$X$ を確率変数， $\mu\in \mathbb{R},\; \sigma > 0$ とする。 $X$ の確率密度関数が

\color{red} p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}

となるとき， $X$ は平均 $\mu$ ，分散 $\sigma^2$ の正規分布 (normal distribution) に従うといい， $\color{red} X\sim N(\mu, \sigma^2)$ とかく。

正規分布のさまざまなまとめについては，以下の記事を参考にしてください。

正規分布の歪度・尖度の導出証明

さて，それぞれについて，導出の証明を行いましょう。

正規分布の歪度の導出

まずは歪度（わいど） $\dfrac{E[(X-\mu)^3]}{\sigma^3}$ を求めます。

確率密度関数を用いる方法
特性関数の微分を用いる方法

の2通りで証明しましょう。

確率密度関数を用いる方法

証明

期待値と確率密度関数の定義から，

\begin{aligned}&E[(X-\mu)^3] \\ &= \int_{-\infty}^\infty (x-\mu)^3 p(x)\, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty (x-\mu)^3 e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx \end{aligned}

$y = x-\mu$ で置換積分すると，

\begin{aligned}&\frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty (x-\mu)^3 e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx\\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty y^3 e^{-\frac{y^2}{2\sigma^2}} \, dy \end{aligned}

である。 $\int_{-\infty}^\infty\bigl| y^3 e^{-\frac{y^2}{2\sigma^2}}\bigr| \, dy < \infty$ に注意して，被積分関数は奇関数であるから，結局，

\frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty y^3 e^{-\frac{y^2}{2\sigma^2}} \, dy = 0

となり， $E[(X-\mu)^3] = 0$ なので，歪度 $\dfrac{E[(X-\mu)^3]}{\sigma^3} = 0$ となる。

証明終

特性関数の微分を用いる方法

まずは，正規分布の特性関数について復習しておきましょう。

正規分布の特性関数

\color{red} E[e^{itX}]= \exp \left( i\mu t - \frac{\sigma^2 t^2}{2} \right)

これの証明については，以下の記事を参照してください。

特性関数の微分により， $X\sim N(\mu, \sigma^2)$ のときの3次モーメント $E[ X^3]$ を求めて， $E[(X-\mu)^3] = E[X^3]+ 3E[\mu X^2]+ \cdots$ としても，もちろん良いです。
しかし，平行移動して， $Y = X-\mu \sim N(0, \sigma^2)$ として， $Y$ の特性関数を求め， $E[Y^3]$ を考えた方が速いため，今回はそうしましょう。

証明

$Y=X-\mu$ と平行移動すると， $Y\sim N(0,\sigma^2)$ となる。 $E[e^{itY}] = \exp\left(\frac{-\sigma^2t^2}{2}\right)$ の両辺 $t$ で3回微分すると，