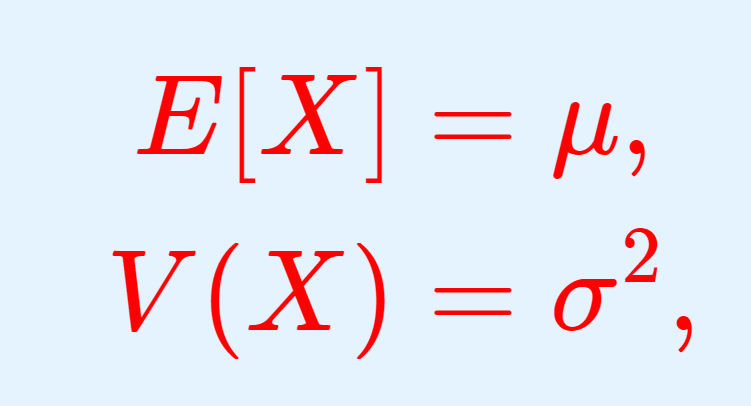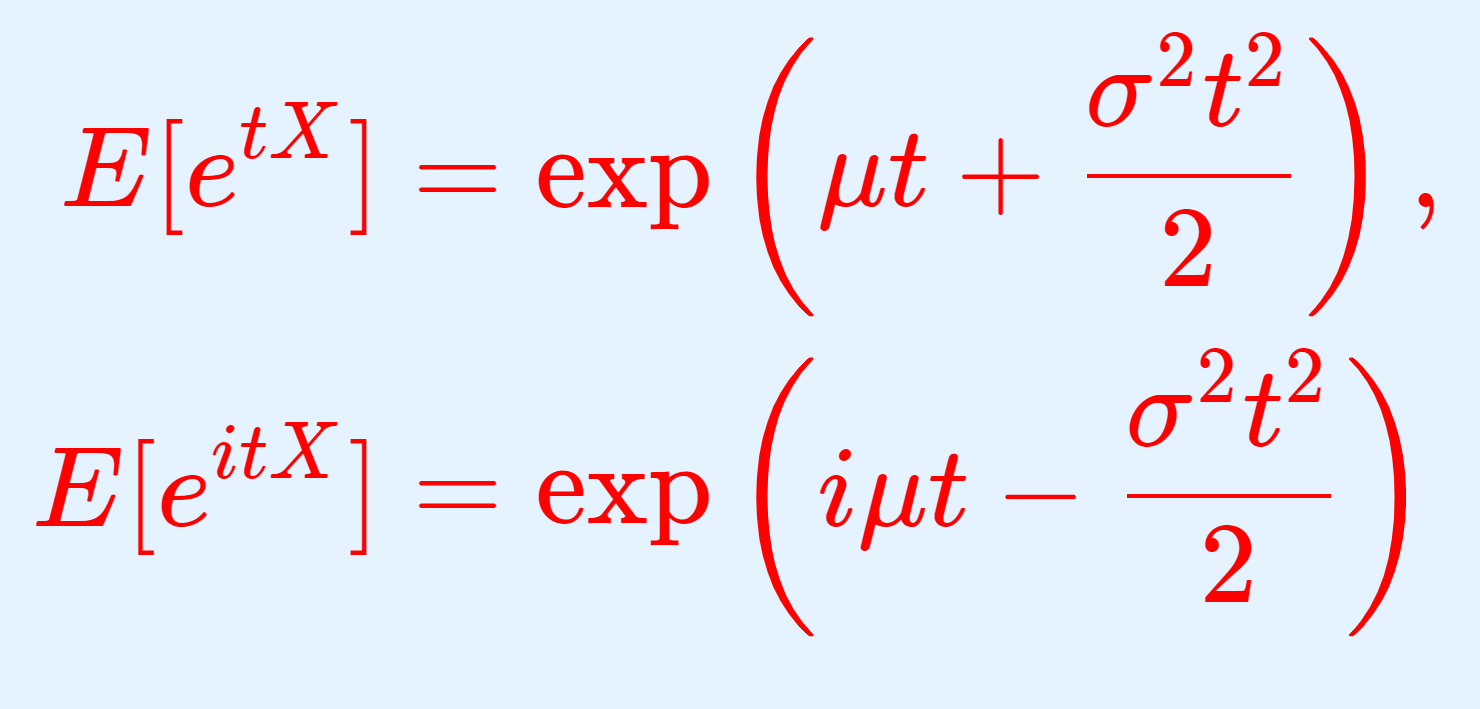正規分布 N(\mu,\sigma^2) の期待値(平均)・分散・標準偏差はそれぞれ
\begin{aligned} E[X]&= \mu, \\ V(X)&= \sigma^2, \\ \sqrt{V(X)} &= \sigma \end{aligned}
となります。これについて,導出の証明を行いましょう。
正規分布の期待値(平均)・分散・標準偏差
まずは結論をもう一度述べましょう。
定理(正規分布の期待値(平均)・分散・標準偏差)
X\sim N(\mu,\sigma^2 ) とする。このとき, X の期待値(平均)・分散・標準偏差はそれぞれ
\color{red} \begin{aligned} E[X]&= \mu, \\ V(X)&= \sigma^2, \\ \sqrt{V(X)} &= \sigma \end{aligned}
である。
証明に入る前に,まずは正規分布の確率密度関数を確認しておきます。
X を確率変数, \mu\in \mathbb{R},\; \sigma > 0 とする。 X の確率密度関数が
\color{red} p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
となるとき, X は平均 \mu ,分散 \sigma^2 の正規分布 (normal distribution) に従うといい, \color{red} X\sim N(\mu, \sigma^2) とかく。
正規分布のまとめについては,以下の記事で解説しています。
なお,確率密度関数と,分散との関係は以下のようになります.
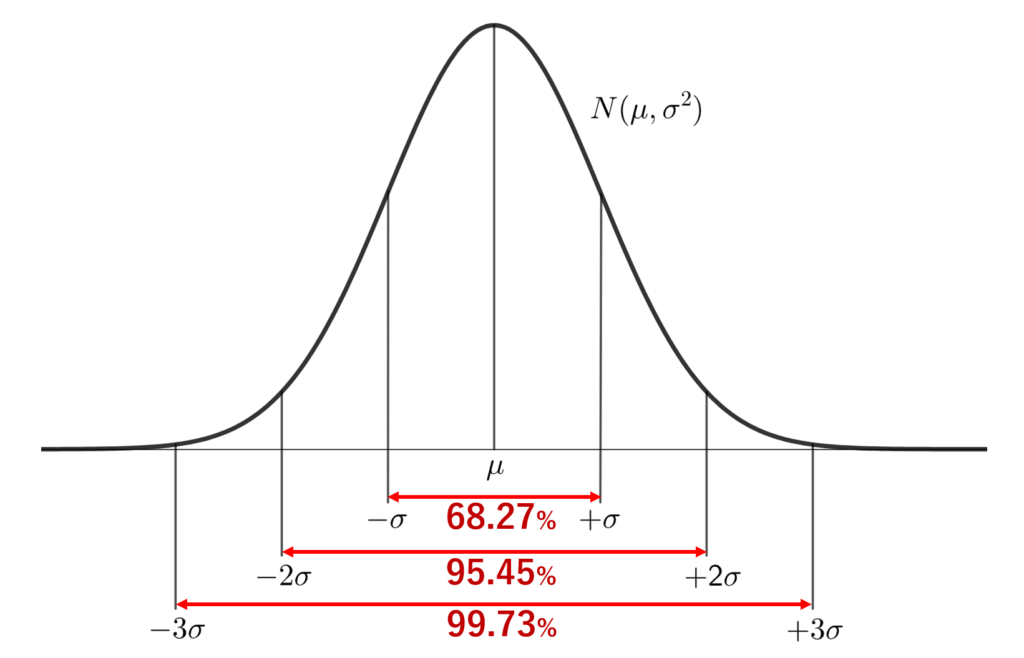
それでは,早速導出していきましょう。
正規分布の期待値(平均)の導出
期待値について,
- 定義から直接証明する方法
- 特性関数の微分を用いる方法
の2通りを,順番に紹介しましょう。
【期待値】定義から直接証明する方法
証明
期待値と確率密度関数の定義より,
\begin{aligned} E[X] &= \int_{-\infty}^\infty x p(x) \, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty x e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty (x-\mu+\mu) e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty (x-\mu) e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx \\ &\quad+\frac{\mu}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty (x-\mu) e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx + \mu \end{aligned}
である。第1項について, y=\dfrac{x-\mu}{\sigma} で置換すると,
ただし,最後の等式は,被積分関数が奇関数であることからわかる。したがって, E[X] = \mu.
証明終
【期待値】特性関数の微分を用いる方法
特性関数の微分を用いて証明する前に,正規分布の特性関数について述べておきます。
これの証明については,正規分布の積率母関数(モーメント母関数)・特性関数とその導出証明を参照してください。
これを用いると,以下のような証明も可能です。
証明
特性関数の式を t で微分すると,
E[iXe^{itX}] = i(\mu+i\sigma^2 t)\exp \left( i\mu t - \frac{\sigma^2 t^2}{2} \right)
となる。両辺に t= 0 を代入すると, E[iX] = i\mu なので,
証明終
なお,今回は特性関数を用いましたが,積率母関数(モーメント母関数)を用いても,同じように証明可能です。
正規分布の分散の導出
続いて,分散の導出を行います。こちらも,
- 定義から直接証明する方法
- 特性関数の微分を用いる方法
の2通りを,順番に紹介しましょう。
【分散】定義から直接証明する方法
分散の定義は, V(X) = E[(X-E[X])^2] = E[(X-\mu)^2] だったことに注意しましょう。
証明
E[X]=\mu より,分散の定義から,
\begin{aligned}V(X)&= E[(X-\mu)^2]\\ &= \int_{-\infty}^\infty (x-\mu)^2 p(x)\, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty (x-\mu)^2 e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx \end{aligned}
y=\dfrac{x-\mu}{\sigma} で置換積分すると,
である。被積分関数を y と ye^{-y^2/2} に分けて部分積分をして,さらにガウス積分を行うと,
\begin{aligned}&\frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^\infty y^2 e^{-y^2/2} \, dy \\
&= \frac{\sigma^2}{\sqrt{2\pi}}\left\{[y \cdot (-e^{-y^2/2}) ]_{-\infty}^\infty + \int_{-\infty}^\infty e^{-y^2/2} \, dy \\ \right\} \\
&=\sigma^2
\end{aligned}
となるから,結局, V(X) = \sigma^2.
証明終
【分散】特性関数の微分を用いる方法
証明には, V(X) = E[X^2]-E[X]^2 を用います。
証明
特性関数の式 E[e^{itX}]= \exp \left( i\mu t - \frac{\sigma^2 t^2}{2} \right) を t で2回微分すると,
\begin{aligned}&E[(iX)^2e^{itX}] \\ &=-(\sigma^2+(\mu+i\sigma^2 t)^2)\exp \left( i\mu t - \frac{\sigma^2 t^2}{2} \right) \end{aligned}
となる。両辺に t=0 を代入すると,
なので,E[X^2] = \sigma^2+\mu^2. ここで,
であり,これが結論である。
証明終
正規分布の標準偏差について
標準偏差の定義は,分散の平方根 \sqrt{V(X)} でしたから,分散が \sigma^2 と導出されたことから,
\sqrt{V(X)} = \sqrt{\sigma^2} = \sigma
であることが分かりますね。