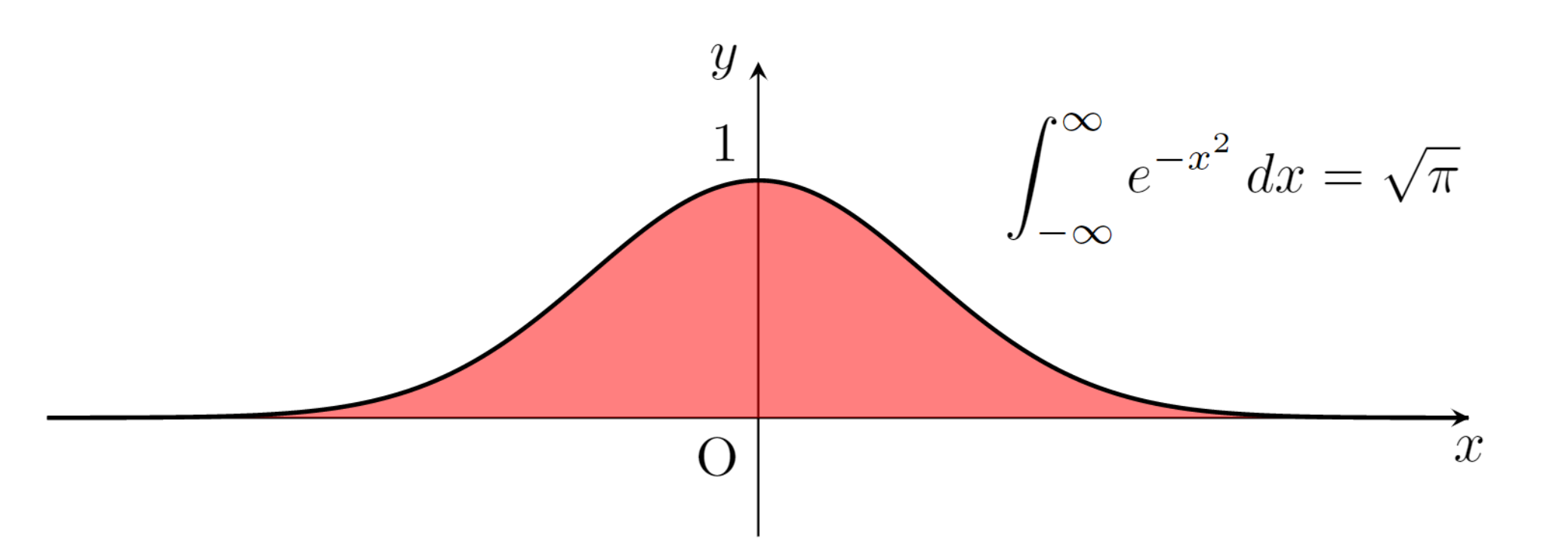
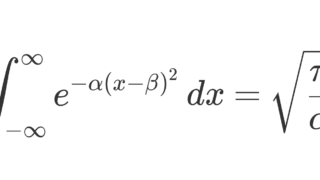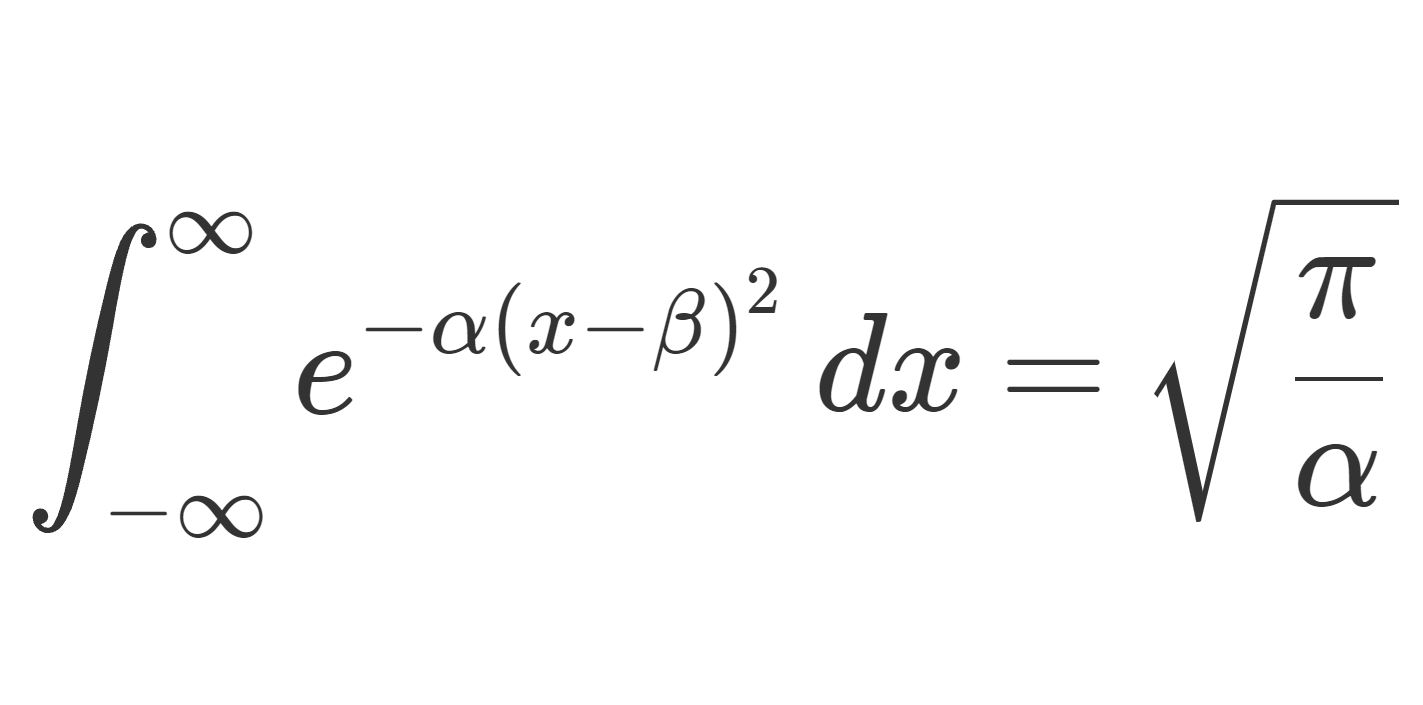ガウス積分のさまざまな形とその証明5つ

ガウス積分 (Gaussian integral) とは，ガウス関数 $e^{-x^2}$ の積分

\int_{0}^\infty e^{-x^2}\, dx = \frac{\sqrt{\pi}}{2}

などを指します。大学1年で扱う，原始関数が初等関数で表せない代表的な広義積分だといえるでしょう。これについて，その公式と証明を行います。

【e^-x^2の積分】ガウス積分の公式
ガウス積分の証明5つ
正規分布への応用
ガウス積分の複素数への拡張
関連する記事
参考

【e^-x^2の積分】ガウス積分の公式

定理（ガウス積分; Gaussian integral）

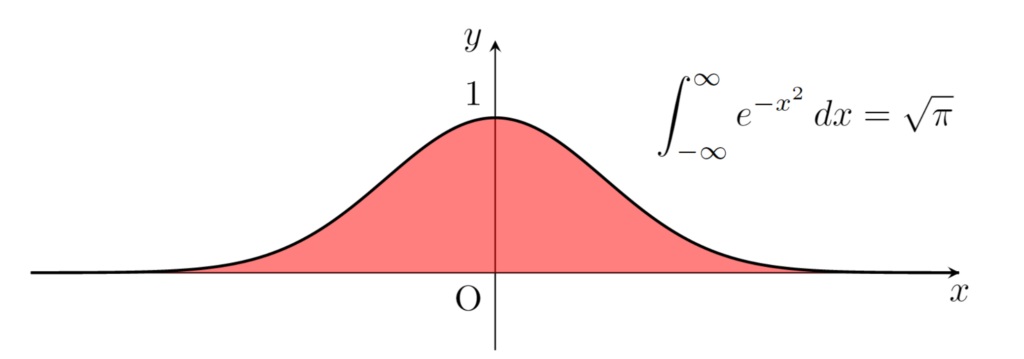
\large\color{red} \int_{-\infty}^\infty e^{-x^2}\, dx = \sqrt{\pi}

である。被積分関数は偶関数であるから，

\large\color{red} \int_{0}^\infty e^{-x^2}\, dx = \frac{\sqrt{\pi}}{2}

も分かり，置換積分 $y^2=ax^2$ により，

\large \color{red} \int_{-\infty}^\infty e^{-ax^2}\,dx = \sqrt{\frac{\pi}{a}},\quad a>0

も分かる。

$e$ と $\pi$ を広義積分でつなげるきれいな公式ですね。また，上の結果から，

$\displaystyle\color{red} \int_{-\infty}^\infty e^{-a(x-b)^2}\,dx = \sqrt{\frac{\pi}{a}},\quad a>0,$
$\displaystyle \color{red}\int_{-\infty}^\infty e^{-(ax^2+bx+c)}\,dx = \sqrt{\frac{\pi}{a}}e^{\frac{b^2}{4a}-c} ,\quad a>0,\;b,c\in\mathbb{R}$

も分かります。2つ目については， $ax^2+bx+c = a\left(x-\dfrac{b}{2a}\right)^2- \dfrac{b^2}{4a} + c$ を使えばよいですね。

なおガウス積分は，原始関数が既知の初等関数でかけません。ガウス積分は，後で紹介する通り確率論などの応用も存在し，原始関数が表せないのは非常に不便です。そこで，

\color{red} \operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\,dt

を誤差関数 (error function) という名前で定義し，用いることがあります。ガウス積分の計算により， $\operatorname{erf}(\pm\infty)=\pm 1$ ですね。

ガウス積分の証明5つ

さて，ガウス積分を証明していきましょう。 $\int_0^\infty e^{-x^2}\,dx= \sqrt{\pi}/2$ か， $\int_{-\infty}^\infty e^{-x^2}\,dx= \sqrt{\pi}$ のどちらかを示せばよいです。

以下で，5つの証明を紹介します。「高校範囲 ${}+\varepsilon$ 」とは，広義積分を認めると，高校生にも概ね理解可能な証明を指します。

証明に関して，一般に非負な関数に対しては，自由に(広義)積分の順序を交換して良い(フビニの定理)ので，積分の順序交換は自由に行うことにします。

1. 極座標変換による最も有名な証明

まずは大学1年生の微分積分学で習うであろう，重積分の極座標変換を用いた最も有名な証明です。有名ですが，正直覚えていないと思いつくのは難しいでしょう。

証明

\begin{aligned}\left(\int_0^\infty e^{-x^2}\, dx\right)^2 &= \int_0^\infty e^{-x^2}\, dx \int_0^\infty e^{-y^2}\, dy \\ &= \int_0^\infty\int_0^\infty e^{-(x^2+y^2)} \, dxdy \end{aligned}

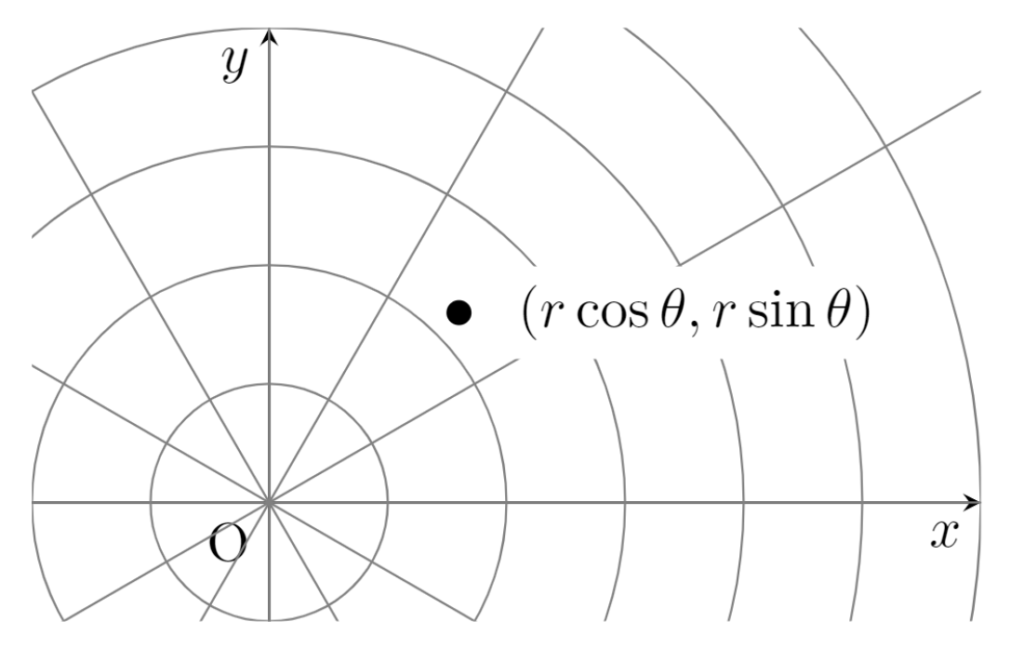
である。ここで， $x=r\cos\theta,\, y=r\sin\theta \; (r>0)$ によって極座標変換すると， $dxdy = r\,drd\theta$ である(→重積分の変数変換の方法とその例題～極座標変換の解説付き～)。よって，

\begin{aligned} &\int_0^\infty\int_0^\infty e^{-(x^2+y^2)} \, dxdy \\ &= \int_0^{\pi/2} \int_0^\infty e^{-r^2}r\,drd\theta \\ &= \int_0^{\pi/2} \left[-\frac{e^{-r^2}}{2}\right]_0^{\infty}\,d\theta \\ &= \frac{\pi}{4}.\end{aligned}

したがって，求める積分の2乗が $\pi/4$ なので，

\int_0^\infty e^{-x^2}\, dx =\frac{\sqrt{\pi}}{2}.

証明終

$\int_0^\infty e^{-x^2}\, dx$ の代わりに， $\int_0^\infty\int_0^\infty e^{-(x^2+y^2)} \, dxdy$ を考えて極座標変換しようという，かなり奇抜な証明です。

2. 1変数の変数変換を用いた高校数学+εの証明

先ほど用いた数式により，再び重積分と見て，それを1変数の逐次積分と思って置換積分することで証明します。

$\tan^{-1} \; (\operatorname{arctan})$ は， $\tan$ の逆関数です(→逆三角関数(arcsin,arccos,arctan)の定義と諸性質まとめ)。

証明

\begin{aligned}\left(\int_0^\infty e^{-x^2}\, dx\right)^2 &= \int_0^\infty\int_0^\infty e^{-(x^2+y^2)} \, dxdy \end{aligned}

までは上と同じ。 $x=yt$ で置換積分すると， $y$ を固定した状態では $dx=ydt$ より，

\begin{aligned} &\int_0^\infty\int_0^\infty e^{-(x^2+y^2)} \, dxdy \\&= \int_0^\infty\int_0^\infty e^{-y^2(1+t^2)} \, ydt dy \\ &= \int_0^\infty\int_0^\infty ye^{-y^2(1+t^2)} \, dy dt \\ &= \int_0^\infty \left[ -\frac{e^{ -y^2(1+t^2)} }{2(1+t^2)}\right]_0^\infty dt\\ &= \int_0^\infty \frac{1}{2(1+t^2)}\,dt\\ &= \frac{1}{2} \left[\tan^{-1} t \right]_0^\infty = \frac{\pi}{4} \end{aligned}

である。2つ目の等式は，積分の順序交換を行った。これにより，求める積分の2乗が $\pi/4$ なので，結論が従う。

証明終

高校生であれば，最後の部分は $x=\tan \theta$ の置換積分と思うことで， $\tan^{-1}$ の議論を避けるとよいかもしれません。

3. ガンマ関数の相反公式を用いた証明

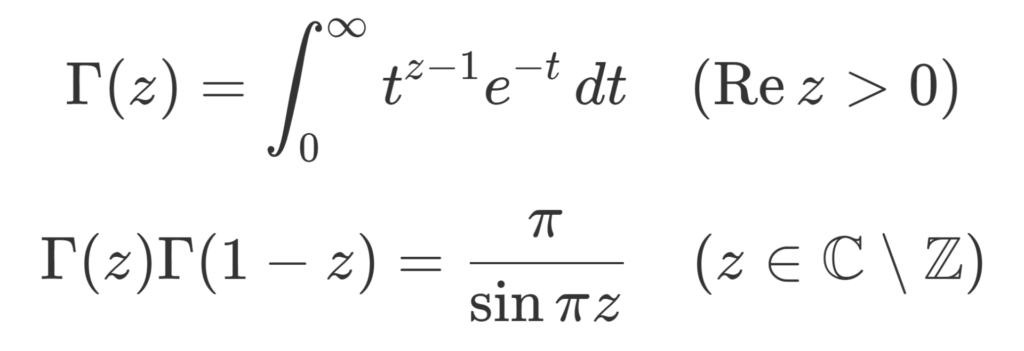
ガンマ関数 $\Gamma(z)= \int_0^\infty t^{z-1} e^{-t}\,dt\;(\operatorname{Re}z>0)$ とその相反公式 $\Gamma(z)\Gamma(1-z)= \pi/\sin \pi z \; (z\in\mathbb{C}\setminus{\mathbb{Z}})$ を用いた証明です。

相反公式は既知とせず，必要となる $z=1/2$ の場合のみ，ベータ関数を経由して証明しましょう。

「ガンマ関数」「ベータ関数」は単に1変数の広義積分ですから，高校生でも比較的理解しやすいと思います。

証明

$u=t^{1/2}$ とおいて置換積分すると，

\begin{aligned}\Gamma\left(\frac{1}{2}\right) &= \int_0^\infty t^{-1/2} e^{-t}\, dt \\ &= \int_0^\infty u^{-1} e^{-u^2}\, 2udu \\ &= 2\int_0^\infty e^{-u^2} \, du \end{aligned}

であるから， $\Gamma(1/2)=\sqrt{\pi}$ を証明すればよい。ここで， $\Gamma(1)=\int_0^\infty e^{-t}\,dt=1$ であることと，ベータ関数との関係式

B(x,y)= \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}

(→ガンマ関数とベータ関数の関係式とその証明)から， $x=y=1/2$ とすることで，

\Gamma\left(\frac{1}{2}\right)^2= B\left(\frac{1}{2},\frac{1}{2}\right) = \int_0^1 \frac{dt}{\sqrt{t(1-t)}}\,dt

となる。 $t=\sin^2\theta$ で置換積分することで，

\Gamma\left(\frac{1}{2}\right)^2 = \int_0^{\pi/2} \frac{2\sin\theta\cos\theta}{\sin\theta\cos\theta}\,d\theta=\pi

となって，証明が終わる。

証明終

4. ウォリス積分を用いた高校範囲+εの証明

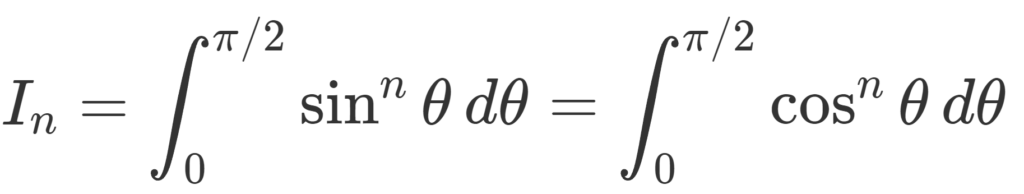
次の証明は，高校範囲でも理解できますが，完全に理解するためには，ウォリス積分・ウォリスの公式の証明も含めて追う必要があるため，長くなります。

証明

$0<x<1$ に対して， $1+x\le e^x\le 1/(1-x)$ が成立するから， $0<x<1$ に対して，

1-x^2\le e^{-x^2} \le \frac{1}{1+x^2}

である。各辺 $n$ 乗して $(0,1)$ 上積分すると，

\!\!\!\! \int_0^1\! (1-x^2)^n\,dx \le\int_0^1 \!e^{-nx^2}\,dx \le \!\int_0^1 \frac{dx}{(1+x^2)^n}.

左辺は $x=\sin\theta$ ，中辺は $x=y/\sqrt{n}$ ，右辺は $x=\tan\theta$ と置換すると，

\small \!\!\!\! \int_0^{\pi/2} \!\!\cos^{2n+1}\theta\,d\theta \le\int_0^{\sqrt{n}} \frac{e^{-y^2}}{\sqrt{n}}\,dy \le \int_0^{\pi/4}\!\!\cos^{2n-2}\theta \,d\theta .

右辺は積分範囲を $(0,\pi/2)$ とし， $2n-2$ 乗を $2n-3$ 乗にしても不等号は変わらない。 $I_n=\int_0^{\pi/2} \cos^n\theta\,d\theta$ とおくと，

\sqrt{n} I_{2n+1}\le \int_0^{\sqrt{n}}e^{-y^2}\,dy\le \sqrt{n}I_{2n-3}.

ウォリス積分により， $I_n$ は計算出来て(→【ウォリス積分】sin,cosのn乗積分の導出と性質)，

\!\!\sqrt{n}\frac{(2n)!!}{(2n+1)!!}\le \int_0^{\sqrt{n}}\!\!e^{-y^2}\,dy \le \sqrt{n} \frac{(2n-4)!!}{(2n-3)!!} .

ウォリスの公式 $\sqrt{\pi}=\lim_{n\to\infty} \frac{1}{\sqrt{n}}\frac{(2n)!!}{(2n-1)!!}$ (→ウォリスの公式3つとその証明)より，上式の各辺 $n\to\infty$ とすることで，

\int_0^\infty e^{-y^2}\, dy= \frac{\sqrt{\pi}}{2}

がわかる。

証明終

なお，測度論における単調収束定理を認めると，ウォリス積分・ウォリスの公式を用いた別の証明が可能です。これについては，【測度論】単調収束定理とその応用・証明の中で解説しています。

5. 回転体の体積を考える証明

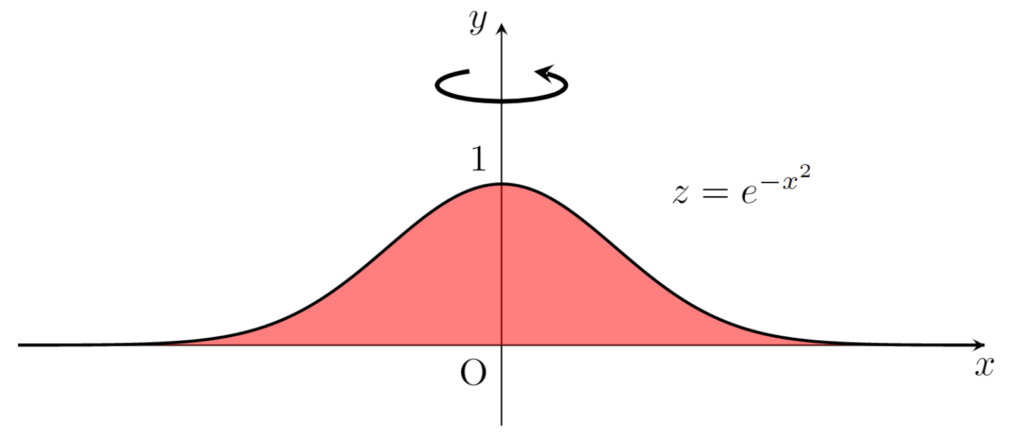
続いて，回転体と， $xy$ 平面で囲まれた部分の体積を考える証明です。

証明

$xyz$ 空間上の曲線 $z=e^{-x^2}, \, y=0$ を $z$ 軸を中心に回転させたときにできる曲面 $z=e^{-(x^2+y^2)}$ と， $xy$ 平面で囲まれた部分の体積 $V$ を考える。

求める立体を， $z$ 軸に垂直な平面でスライスした平面の断面積を $S(z)$ とすると，これは円であり， $e^{-x^2}\iff x^2= -\log z \; (0<z<1)$ であるから， $S(z)=\pi x^2= -\pi \log z$ となる。したがって，求める体積は

\begin{aligned}V&=\int_0^1 S(z)\,dz \\ &=\int_0^1 (-\pi\log z)\,dz \\ &= -\pi \left[ z\log z - z\right]_0^1 = \pi .\end{aligned}

一方で， $x$ 軸方向にスライスして，その断面積を $A(x)$ とすると，

\begin{aligned} V&= \int_{-\infty}^\infty A(x)\,dx \\ &= \int_{-\infty}^\infty \left(\int_{-\infty}^\infty e^{-(x^2+y^2)}\, dy\right)dx \\ &= \int_{-\infty}^\infty e^{-x^2}\, dx \int_0^\infty e^{-y^2}\, dy\\ &= \left(\int_{-\infty}^\infty e^{-x^2}\, dx\right)^2 .\end{aligned}

以上から，

\int_{-\infty}^\infty e^{-x^2}\, dx =\sqrt{\pi}.

証明終

後半は，一番最初の証明の冒頭を，図形的に捉えただけですね。

広義積分にならないよう，積分範囲を区切って考えれば，高校生でもある程度できそうですね。

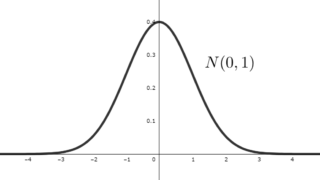
正規分布への応用

ガウス積分が最も応用される場所が，確率論における正規分布でしょう。平均 $\mu$ ，分散 $\sigma^2$ である正規分布 $N(\mu,\sigma^2)$ の確率密度関数は

p(x)= \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\quad x\in\mathbb{R}

となります。全体の確率が $\int_{-\infty}^\infty p(x)\,dx=1$ となることは，ガウス積分から容易に確認できるでしょう。正規分布については，以下の記事で詳しく解説しています。

ガウス積分の複素数への拡張

ガウス積分は，複素数へと拡張することが可能です。それが以下の定理です。

定理（複素ガウス積分）

$\operatorname{Re} \alpha > 0,\, \beta \in \mathbb{C}$ に対して，

\int_{-\infty}^\infty e^{-\alpha(x-\beta)^2}\,dx=\sqrt{\frac{\pi}{\alpha}}

が成り立つ。

これについては，以下で証明しましょう。

【e^-x^2の積分】ガウス積分の公式

ガウス積分の証明5つ

1. 極座標変換による最も有名な証明

2. 1変数の変数変換を用いた高校数学+εの証明

3. ガンマ関数の相反公式を用いた証明

4. ウォリス積分を用いた高校範囲+εの証明

5. 回転体の体積を考える証明

正規分布への応用

ガウス積分の複素数への拡張

関連する記事

参考